An anomaly, in quantum field theory jargon, is the lack of a symmetry of a physical system at the quantum level, when the same system before quantization does possess that symmetry. The loss is due to the rules of the quantum world, and studying in detail similar situations does allow us to understand more of those, as well as to verify that our theory is indeed a faithful representation of physical reality.
In the case at hand we are talking about the magnetic dipole moment of an elementary particle. If we think at the electron as a charged sphere rotating along one axis, we have no problem understanding that it must generate a magnetic field: the magnetic force is always produced by moving (in this case, rotating) electrical currents. But the electron is a point-like particle, so the idealization of a charged sphere loses appeal; even more so does the classical idea of spin. Nevertheless the electron has a spin, and it consequently has a magnetic moment, which can be computed with an equation discovered by Paul Dirac more than 80 years ago. And that magnetic moment is anomalous, as its value differs from the classical value for a Dirac pointlike particle of charge e and spin one-half.
The calculation of the electron's magnetic moment is serious business. As the experimental value has reached a precision of few tenths per billion, thanks to a recent Harvard University measurement, theory must produce a similarly precise number in order to make the comparison a meaningful one.
Now a paper by Japanese theorists Aoyama, Hayakawa, Kinoshita, and Nio details a calculation of the contribution to the "electron anomaly" (the difference of the moment from the classical theory prediction) of several thousand diagrams at tenth order in perturbation theory. This means that there are a total of 10 vertices in the diagrams describing the "electron-photon vertex". The physicists calculated a class of diagrams, not all of them; they focused on the class of diagrams where there are no closed lepton "loops": such diagrams are the hardest ones to evaluate. they involve huge integrals which require some automation to be carried out in large numbers. There are 6354 of them.
Getting to tenth order in perturbation theory was necessary because the experimental measurement of the anomaly gives a_e = (1159652180.73 +- 0.28)x 10^(-12). If one compares this to the fifth power of the fine structure constant divided by pi, (α/π)^5=0.07 x 10^(-12), one realizes that stopping to eight order (i.e., a fourth power of a/p) would give too little accuracy in the theoretical prediction.
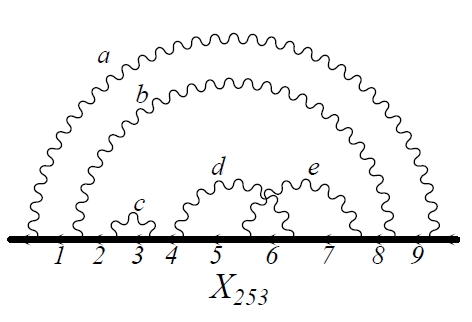
The Feynman diagrams evaluated by the authors can be classified according to the "topology" of the photon lines that constitute them. One has an electron line (time flowing from left to right) and this line "emits" photons (semicircles), later reabsorbing them. A look at the picture below, which shows only a part of the topologically distinguishable diagrams, is enough to give you a headache, if you understand what they really mean. A double headache, if you also know that to compute the contribution of each means a week of work on a blackboard...

If your eye does not catch the difference between each of the small diagrams in the picture above, you can understand what is going on better by looking at one diagram zoomed in: the wiggly lines are photons, the straight line is the electron.
Authors are adamant about the fact that their achievement is remarkable. They in fact write
"In view of the enormous size and complexity of the integrals of Set V, it is unlikely that the validity of our results can be tested by an independent method any time soon. We are thus obliged to establish their validity to the best of our capability."
Which they do in a separate section of the paper. If you want to check it, the paper can be found at this link. The final result of adding the calculated diagrams contribution to previously measured results for the other classes of diagrams is the following: the anomaly is predicted to amount to a_e = 1159652181.643 x 10^(-12), with a total uncertainty of about 0.77, driven by the hadronic and electroweak diagrams contributions.
All in all, we can well say that the more we dig, the more the standard model appears to be "the" theory of fundamental interactions -at least at the energy scales and precision levels we are capable of testing today.




Comments