(Previous post: http://www.science20.com/gem_1-127962)
Precession of a planetary orbit
We will use the Lagrangian:
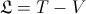
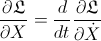
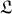 – Lagrangian
– Lagrangian
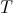 – kinetic energy
– kinetic energy
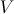 – potential energy
– potential energy
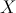 – space-coodrinate
– space-coodrinate
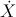 – time derivative of
the space-coordinate
– time derivative of
the space-coordinate
We are not going to derive the orbit of the planet – we know that the ideal orbit of a planet is ellipse:
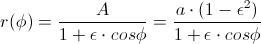
An example of how it is derived using the Lagrangian you can see in this document: http://www.math.washington.edu/~morrow/papers/Genrel.pdf
We are going to focus just on the precession,
that is, we are going to focus on the coordinate 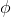 , first in the classical way, and then by using the length and time equations
derived in the previous post “The gem (1)”.
, first in the classical way, and then by using the length and time equations
derived in the previous post “The gem (1)”.
So, let’s do it.
Classical calculation:
- position of the planet
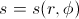
- velocity
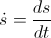
– kinetic energy
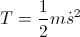
– gravitational potential energy
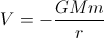
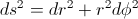
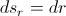
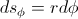
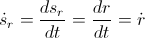
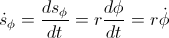
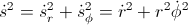
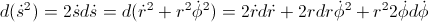
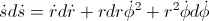
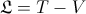
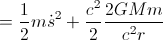
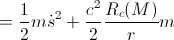
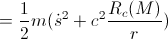
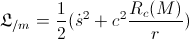
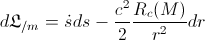
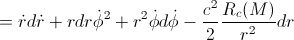
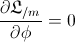
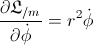
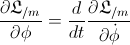
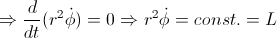
(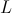 is the well known constant of motion: the angular
momentum)
is the well known constant of motion: the angular
momentum)
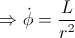
So, by using the classical calculation, we’ve got that
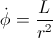
But, when we take into account the gravitational influence (derived in the previous post “The gem (1)”), we have:
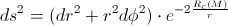
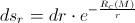
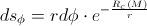
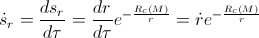
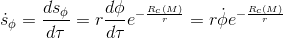
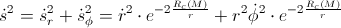
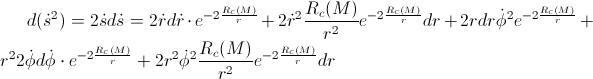
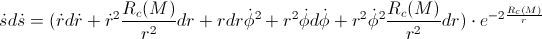
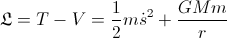
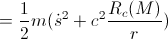
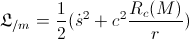
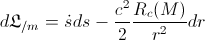
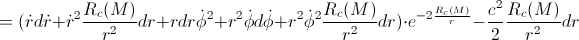
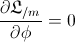
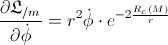
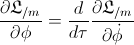
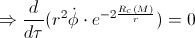
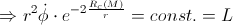
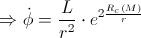
By applying the classical calculation, we’ve got that
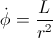
Let’s denote the \phi in the classical calculation as
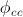 . So,
. So, 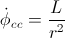
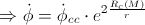
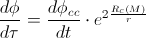
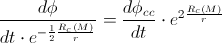
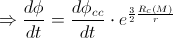
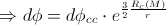
In the classical case, there is no precession:
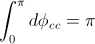
But, in this case (where we’ve used the length and time equations derived in the previous post “The gem (1)”), we have the precession, and it can be calculated as:
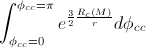
Since 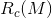 is very small comparing to the planet-orbit-radius
is very small comparing to the planet-orbit-radius 
(i.e. for the Sun, 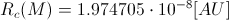 ),
),
we can simplify the calculation in the following way:
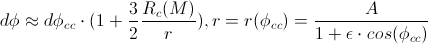
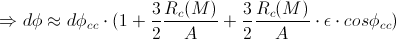
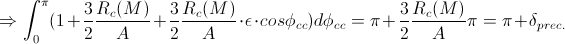
So, the precession-angle per half-revolution is:
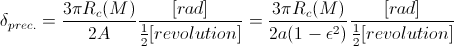
Now, let's calculate the precession angle for Mercury:
http://en.wikipedia.org/wiki/Mercury_(planet)
http://www.met.rdg.ac.uk/~ross/Astronomy/Planets.html
http://www.math.washington.edu/~morrow/papers/Genrel.pdf
- semi-major axis: 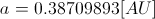
-
eccentricity: 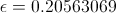
-
revolutions per century: 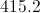
-
observed precession: 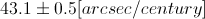

In the next post: Shapiro time delay



