Photon’s delay in the gravitational field
In
the post “The gem (1)”, the equation for photon’s velocity was derived, which tells
us that the photon’s velocity is not constant in the gravitational field:
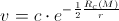
Before the equation for photon’s velocity, the equation for gravitational time was derived:
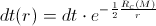
From these two equations, followed the equation for the photon’s path-element:
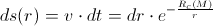
The
Earth’s gravitational influence on the speed of light is practically
neglectable. Namely, if we take that the speed of light is 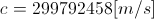 , then,
according to the equation
, then,
according to the equation
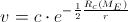
on
the Earth’s surface it would be 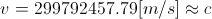
Even If we encounter the influence of Sun, the velocity of a photon would be
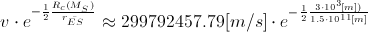
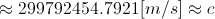
But,
very near the Sun’s surface, it would be 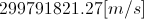 ,
which is
,
which is 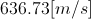 less than
less than  .
.
Let’s assume that a photon travels from Earth to Mars and back, along some path which passes very near the Sun surface.
If the speed of light would be constant, the photon would travel from Earth to Mars and back for some time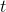 . But,
according to the equation
. But,
according to the equation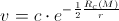
it should travel longer, for some time
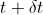
So, let’s calculate the
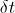
The path-element of a photon is
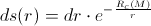
Along the path
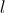 , we’d
have
, we’d
have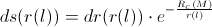
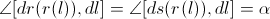
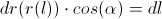
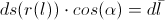
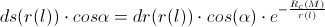
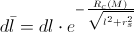
 for
Sun is approximately 3 km.
for
Sun is approximately 3 km.The minimal value for
 is
is 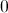 , so we have that even the maximal value of
exponent is very, very small
, so we have that even the maximal value of
exponent is very, very small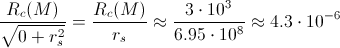
Hence, for our calculation, it is sufficient to take just the first two terms of the Taylor series for the function
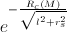
that is,
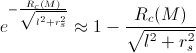
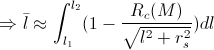
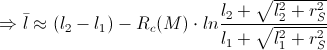
Let us divide the photon’s route in four sub-routes:
 ,
,  ,
, 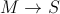 ,
, 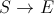
Let us first consider the last sub-route
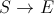
If we take the point 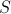 to be the coordinate origin, and the direction of
to be the coordinate origin, and the direction of 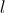 -axis from
-axis from 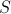 to
to 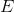 , we’d have
, we’d have
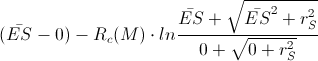
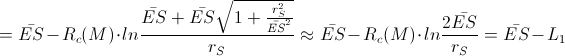
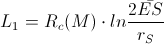
The additional short distance 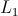 which our photon has to travel is in the
Earth’s vicinity. That is very far from Sun, so along the distance
which our photon has to travel is in the
Earth’s vicinity. That is very far from Sun, so along the distance 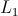 we can consider that the velocity of our
photon is practically
we can consider that the velocity of our
photon is practically  .
.
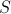 to
to 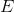 is
is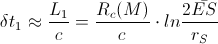
The sum-time-delay along the last sub-route
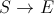 and the along first
sub-route
and the along first
sub-route 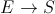 would be
would be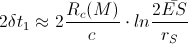
The sum-time-delay along the second sub-route
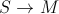 and the third sub-route
and the third sub-route 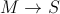 would be
would be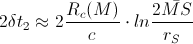
The total time delay would be
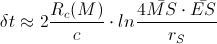
Pic2
If we use these data (the data from Shapiro experiment, shown in the Pic2), we would get the time delay which Shapiro got in his measurement:
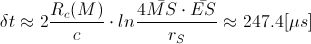
(Google: “Earth Mars Shapiro time delay”)



