Gravitational deflection of light
To calculate the deflection of light which propagates through the medium whose refraction index is continuous, the differential form of Snell’s law is used.
In the case of the gravitational field, as it is given in http://home.fnal.gov/~syphers/Education/Notes/lightbend.pdf
, page 2, equation (6)
the differential form of the Snell’s law is: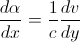
Actually, it should be:
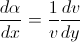
( so, instead of the constant 
, it
should be 
)
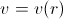Let us write it as
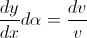
If we take that the velocity is
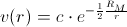
( where 
),
then the solution of the differential equation
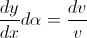
yields the deflection which is two times less than the one which is measured experimentally.
That is not because the equation
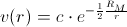
is wrong (it is definitely correct, irrefutably correct), but because the Snell’s law does not take into account the following fact:
Greater the energy of a photon, greater the refraction:
The energy of a photon in a gravitation-field is
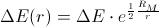
If a photon moves away from gravitation-source, the energy of that
photon decreases (gravitational red-shift, Pound-Rebka experiment).
If a photon moves towards gravitation-source, the energy of that photon increases.
And that energy increase does contribute to the photon’s path deflection.
How much?
Well, we have that
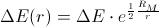, and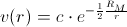
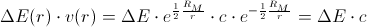
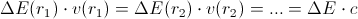
So, for a photon which moves through gravitation-field, we have
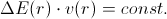
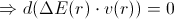
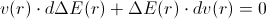
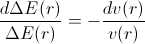
Moving towards the gravitation source,
-
the change of photon’s energy is positive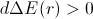 
-
the change of photon’s velocity is negative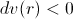 
As for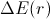 
and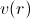 
, they are
inherently positive.
So, we have:
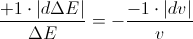
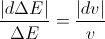
Now, let’s get back to the equation
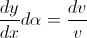
It takes into account only the contribution of the change of the photon’s velocity. By taking into account the contribution of the change of photon’s energy, which – as shown – is equal to the contribution of the change of the photon’s velocity, the differential equation becomes:
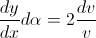
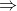
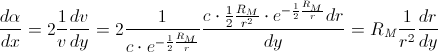
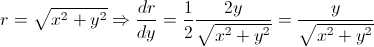
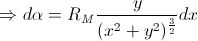
Upon integration, it yields
wher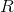e 
is the distance of closest
approach to the gravitation source.
