Today, however, I would like to do here for you what most phenomenologists are doing on their blackboards these days: take the two measurements of the B_d decay to μμ pairs by CMS and LHCb, and combine them in a quick-and-dirty way, and then use that result to speculate on what the combination can be taken to mean - or not.
The motivation for the exercise is provided by figures such as the one below, which have been a common exercise among theoretician friends as of late: compare the limits - and now the measurements - on these branching fractions to the values that would be predicted by alternative models for new physics. The figure is taken by a paper by David Straub (arxiv:1205.6094).
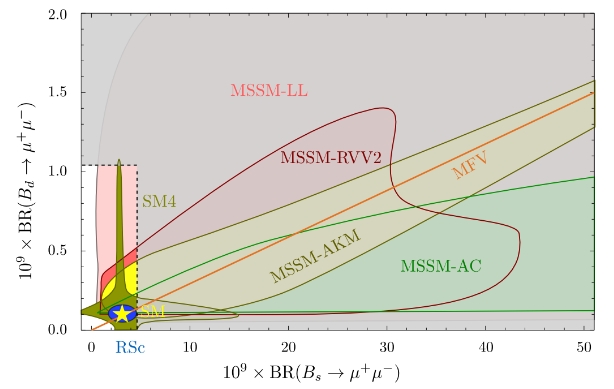
In the figure the branching ratio of the Bs and Bd to dimuons (in 10^-9 units) predicted by the SM (yellow star) is compared to possible values that the two quantities take in varions versions of new physics models. Notably, MSSM predictions extend all over the place, while the "SM4" version - a model with four generations of matter fields - provides either an enhancement (or a deficit) of the Bs decay rate, or an enhancement (or deficit) of the Bd decay rate, but not of both. The box at the lower corner indicates the allowed region of parameter space following limits on the branching fractions determined last year.
I have already explained in some detail in the former post why the rare decay of a neutral B hadron to a muon pair is sensitive to the existence of new physics beyond the standard model. In a nutshell, it is because new very heavy particles (ones we might not have had a chance to discover yet) would contribute significantly to the probability of such decays. Their being very heavy does not keep them from contributing, in fact, because they take part in the decay within virtual quantum loops. A basic course of quantum field theory would allow you to understand in fact that when you need to compute the probability of a reaction A->B you need to sum the amplitudes of all possible processes that bring the state A into the state B. So if one may conceive a new particle circulating in a quantum loop intermediate between state A and state B, that will contribute to the total probability, in some way.
So, since there are only few requirements on the kind of particles that can contribute to the B hadron decays to muon pairs, the range of new physics models that can be tested is wide. The graph shows that a bunch of them does predict enhanced (but even reduced, due to interference effects, in some cases) branching fractions.
Let us then give a look at the most recent measurements of LHCb and CMS. CMS reports
B(Bs->μμ) = (3.0+1.0-0.9) x10^-9
B(Bd->μμ) = (3.5+2.1-1.8) x10^-10
and LHCb reports
B(Bs->μμ) = (2.9+1.1+0.3-1.0-0.1) x10^-9
B(Bd->μμ) = (3.7+2.4+0.6-2.1-0.4) x10^-10.
(the second uncertainty quoted for LHCb is systematical).
The above measurements are not on equal footing: while the Bs ones are based on well-observed signals, with significances of 4.3σ and 4.0σ respectively, the Bd ones are both based on 2.0σ signals only. Nevertheless, if one believes that the Bd decay is there, with a non-zero rate, then one can tentatively use the measurements anyway - while keeping the caveat in mind.
The two experimental results are based on different data and different detectors, but share some common systematic uncertainties - most notably, ones on some structure functions for the decay, which enter the equations because both CMS and LHCb measure the branching fractions by comparing the observed decays to the number of decays to dimuons to others much more frequent, the ones of the B+ meson to J/ψ K+ pairs. Because of that, the exercise of combining the numbers is not trivial if done correctly. Further, the error bars are asymmetric, and so one should combine the likelihood functions from which the measurements are derived rather than the measurements themselves.
Despite all the above, I believe that a quick-and-dirty weighted average will end up being only marginally different from the result of a more accurate determination. And since I am lazy, I will discuss here the result of the simple weighted average (which, I remind you, assumes that the inputs are totally uncorrelated and that they are Gaussian distributed: neither assumption holds). [Disclaimer: Please note that I am doing this exercise just as anybody could, without using any internal information from my experiment (CMS) or the other experiment. What I am doing here for you, anybody can do on the back of an envelope! Also, the facts that I am a member of the CMS collaboration and the fact that I am publishing these publically-available numbers here have exactly zero mutual dependence. I am speaking for myself here!]
So if you average the two results you obtain
B(Bs->μμ) = (2.95 +0.75 -0.67) x 10^-9
B(Bd->μμ) = (3.6 +1.6 -1.38) x 10^-10
Again, bear in mind that the errors above are slightly underestimated - they do not account for positive correlations - and are approximate also because they do not treat the asymmetric errors in a proper way. I believe that the central values, on the other hand, are not going to be much different if one does the exercise correctly, because LHCb and CMS ended up with extremely similar inputs !
So let us compare the above "estimates" with the predictions of the Standard Model: for the Bs the SM predicts B=(3.56+-0.30) x 10^-9 and for the Bd the SM predicts B=(1.07+-0.10) x10^-10. We thus see that the Bs rate is in perfect agreement with the standard model, while our quick-and-dirty weighted average of LHCb and CMS results for the Bd branching fraction turns out to be 3.5 times larger than the prediction.
Is that something worth speculating that we are seeing the first indications of new physics ? This question was somehow asked by a reader in the comments thread of the former post.
My answer ? I doubt it, and for several reasons.
First of all, this is just a less than 2-sigma departure (and we have anyway underestimated the uncertainty due to our sloppy averaging above: when neglecting positive correlations that is a fact).
Second, the effect is based on results which are not yet of observation-level quality.
Third, there is an implicit trials factor of four in the probability that we observe a departure, since we could have been just as surprised to see a deficit, or to see an excess or a deficit in the Bs result (compare to the "cross-like" region of SM4 allowed models in the graph above); a p-value corresponding to less than 2-sigma multiplied by four is a p-value of one-point-something sigma, i.e. one hardly worth discussing!
And Fourth, most models of new physics do not predict an enhancement in the Bd decay to dimuons but a straight-on-the-SM rate of decay to dimuons of the Bs. But then, if we like the four-families extension of the Standard Model, things are different.
As was noted by Masaya Kohda at the EPS 2013 conference last Friday, if we assume that there are four generations of quarks, we need to also assume that the new-found Higgs boson at 125.5 GeV is an impostor - a true Higgs boson would enhance its production rate by a factor of nine (!) in the presence of more than three ordinary generations of quarks, because each new generation provides a contribution in another quantum loop, the one existing between two colliding gluons and the Higgs which provides for the largest part of the production probability of the Higgs at the LHC.
So provided we are ready to make all those steep assumptions - that the particle at 125.5 GeV is not a Higgs and that there are new quarks out there to be found, then a x3.5 rate of Bd decays to dimuons does fit well with a four-generation quarks model.
So... Are you a believer or not ?




Comments