For today, I am happy with a simple illustration of why to be a physicist you need to know basic Statistics. The example is of course based on a real analysis in particle physics. It is based on a claim made in 1969 by McCusker and Cairns that they had observed the track of a special charged particle in a bubble chamber exposed to energetic air showers. The track appeared to ionize the gas of the chamber less than half as much as what it should have: 110 droplets along a unit-length path instead of 229.
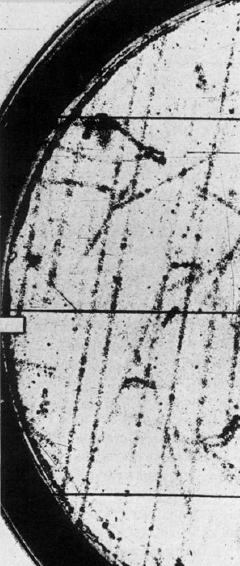 Ionization is (well, was) measured in bubble chambers by counting with a microscope the number of droplets along the particle path. These droplets form by condensation around the points where the incident particle scatters with the gas of the detector.
Ionization is (well, was) measured in bubble chambers by counting with a microscope the number of droplets along the particle path. These droplets form by condensation around the points where the incident particle scatters with the gas of the detector. The figure on the right, taken from PRL 23 (1969), page 658, shows a bunch of parallel tracks caused by a shower of charged particles from a energetic cosmic ray. Among the tracks there is one which is much fainter than the others (I leave you to guess which one it is): that is the one which McCuster and Cairns claimed to be due to a fractionally charged particle.
The question one must answer, in order to start fiddling with the idea that the track in question is due to a free quark or some other exotic thing produced in the very high-energy interaction in the atmosphere, is how likely it is that one observed, among 55,000 tracks, one track with 110 or fewer droplets per unit path length, when the average expected number is 229 (the latter determined by studying the total sample of tracks).
I can hear some of you radiating confidence as you think: "Ah! A simple problem in Statistics... The number of droplets is a Poisson variable, since the Poisson distribution describes the probability of finding n events in a given time, if these occur independently from a constant rate process". Very good then: what you have in mind is the formula
P(n) = [mu^n e^(-mu)]/n!
where mu is the average number in the given time (or given path length, in our case). If for a track we observe n=110 when mu=229, we may ask "What is the probability that a track produces less than 111 droplets, if the expected number of droplets is 229?". The required probability is the sum of P(n) with n running from 0 to 110, and the result is P(n<=110) = 1.6 x 10^(-18).
Okay, then if we have 55,000 of these, the total probability to observe one or more of these is P(>=1 weird track in 55000) = 1-[1-P(n<=110)]^(55000), which is in the whereabouts of 10^-13. One in ten thousand billions! That must surely be a fractional-charge particle ! We are surpassing the five-sigma "observation-level" significance head, shoulders, and tail here.
Hmmm, not so fast.
If you are a good physicist, you know that a single scattering of a charged particle off a nucleus in the vapour of the chamber produces more than a single droplet. In fact, this number is four, on average. The droplet production is itself a Poisson process. Fine, so we have two separate Poisson processes - particle scattering, and droplet formation. Does it change the picture ? No, if you are a good physicist who does not know squat about Statistics.
If you have at least a good hunch of basic Statistics, however, you know that what you are describing is not a simple Poisson process, but a compound Poisson process. And the two are rather different things. The fact that scatterings yield an average of four droplets in fact dramatically increases the likelihood of tracks with small droplet multiplicity: by using the correct distribution function of the compound Poisson (where now mu=4, lambda*mu=229, and N is the number of scatterings):
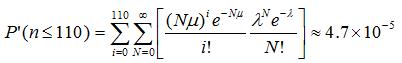
If we then ask what is the chance to have seen at least one such low-ionization track in the 55,000 sample, the probability is now 1-(1-P')^(55000), which is a striking 92.5% ! Ooooops! We should have rather been surprised to NOT have observed such a low-ionization track!
The summary of this example is simple to spell: You may know your detector and the underlying physics as well as you know your ***, but if you do not know basic Statistics you are going to be fooled !
The McCusker and Cairns PRL article soon received its due rebuttal [R.Adair and H.Kasha, PRL 23, 1355 (1969)]. For an evidence of quarks, one would have to wait five more years...




Comments