Both players simultaneously make one of three gestures representing rock (clenched fist), paper (open hand) or scissors (index and middle finger apart). Rock gets beaten (wrapped) by paper, paper gets cut by scissors, and scissors get smashed by rock. Identical gestures create a tie. The objective is to select a gesture that beats that of the opponent.

Rock beats scissors beats paper beats rock beats...
Why should you be interested in this little kid's game? There are many reasons.
Firstly, the game is arguably the simplest possible that contains many of the interesting features of more complex games. The lessons learned from RPS translate directly into games like poker. Some of these lessons have astonished poker theoreticians, and caused a revision in poker theory.
Secondly, although the game is straightforward and possesses a trivial strategy that is unbeatable, the game is ridden by paradoxes. Key to these paradoxes is the competitive cycle that forms the heart of RPS.
Thirdly, nature is full of competitive cycles, and RPS can be seen as the prototypical model to describe the evolutionary dynamics related to such cycles. As we will see, RPS elucidates the concept 'survival of the fittest' and more in particular makes it clear that 'the strongest' need not be 'the fittest'.
Lastly, the simple RPS game appears to be a perfect model case to elucidate the limits of applicability of game theory.
In this blogpost we will dive into the game-theoretical aspects of RPS, and introduce a twists to the game. The resulting 'twisted rock-paper-scissors' game is shown to feature some surprising behaviors.
In follow-up post we will utilize twisted RPS to model a variety of situations. For instance, we will explore what twisted RPS can tell us about the survival of species locked in a competitive cycle. Also, we will use twisted RPS to explain a counter-intuitive feature of multi-person zero-sum games such as poker.
Meeting the Nemesis
How best to play RPS? Key to proper RPS play is to be unpredictable. The slightest sliver of predictability, the tiniest correlation between subsequent moves will make your play vulnerable. The reverse is also true. Be as random as the throw of a die, and select each next move, rock, paper or scissors, at random and with equal probability, and you can face the Nemesis. Your most-feared opponent, the ultimate RPS player who has the capability to exploit any pattern in your moves. This Nemesis can not hurt you. You are unpredictable and thereby unbeatable.

All that you need to be unbeatable
Sounds easy, right? In practice, reaching complete unpredictability is far from easy. At an RPS tournament you have no dice at your disposal. And without a source of randomness, it is virtually impossible to act fully at random. We humans need a motivation for our actions, and by basing our choices on motivation, we tend to become predictable.
Why not give it a try? Here you can play RPS against a computer adversary. Play till either you or the computer has beaten the other 50 times. How do you fare against the computer? Are you losing? Any doubts that this computer program might be cheating? It must have been easy for the programmer to let the algorithm peek at the choice you enter, isn't it?
When consoling yourself with such thoughts, try the following. Reset the score counter and play again many tens of games against the computer. This time, however, you use a die. When you throw a 1 or a 2 you play rock, at a 3 or a 4 your choice is paper, and on a 5 or a 6 you select scissors. Don't overrule the die. Just be a slave to random faith. How are you doing now? Chances are that within statistical fluctuation you are in a tie with the computer.
Still doubting the honesty of the program? This piece of software can't know when you are using a die or when you aren't. If it beats you when you are left to your own choices, and it fails to beat you when you are using a die, it must be that you are playing a poorer RPS game than a dumb die.*
Nash: if you don't move I won't move
The game-theoretical prescription of both players making unbiased random moves constitutes the Nash equilibrium in this game. A Nash equilibrium is characterized by the fact that no individual player can benefit from deviating from the equilibrium strategy. As RPS is a symmetrical zero-sum game,** this means that at the Nash equilibrium neither player loses or gains.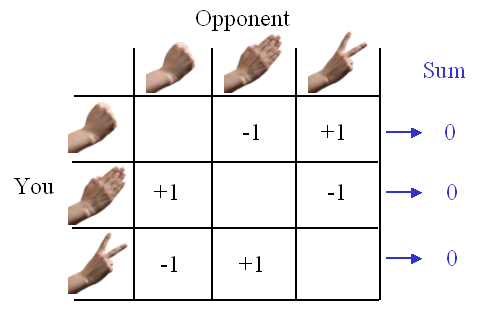
The Nash equilibrium of RPS. If your opponent makes unbiased random choices, none of the choices available to you would lead to an expected gain.
Breaking the symmetry
To proceed, we need to generalize the game somewhat by giving it a twist. 'Twisted RPS' is like standard RPS, but with the added feature of a broken symmetry between the three strategic choices. This symmetry breaking is realized by rendering the pay-off from the game dependent on who is beating who. An example is shown below.
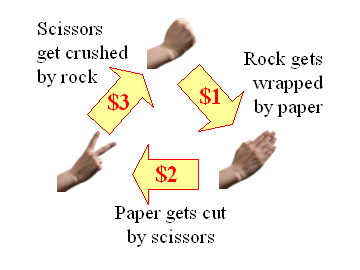
An example of 'Twisted RPS' - Rock gets wrapped by paper but this not hurt very much: rock pays paper $1, paper gets cut by scissors and this hurts more: paper pays scissors $2, scissors get smashed by rock - a costly affair: scissors pay rock $3.
How would you play this twisted variant of RPS?
Obviously, it becomes much less attractive to select 'paper'. If you win (your opponent happens to choose rock) you gain $1, whilst a loss (your opponent happens to select scissors) costs you as much as $2. Compare this to 'rock': if you win you gain $3, whilst a loss costs you no more than $1.
So you reduce the frequency of selecting 'paper'. Right?
Wrong.
Let's see what game theory tells us. Twisted RPS is still characterized by a single Nash equilibrium, and that equilibrium constitutes of weighted random choices. We got that right.
However, a quick inspection (see figure below) reveals that we have to increase the frequency at which we select 'paper' (to a frequency of 1 in 2). This frequency is higher than the number of times we should select 'rock' (which stays at 1 in 3).
Can you explain this counter-intuitive result?
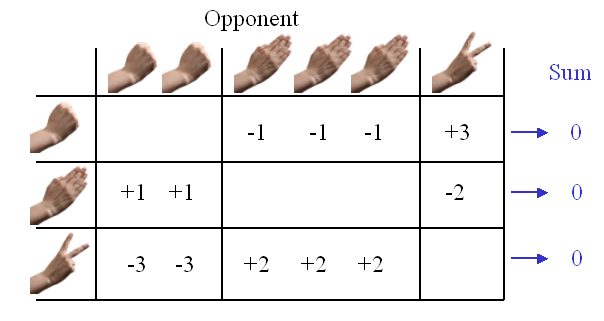
The Nash equilibrium of 'Twisted RPS'. If your opponent makes properly weighted random choices (2 out of 6 times rock, 3 out of 6 times paper, and 1 out of 6 times scissors), you can not make any choice that would lead to an expected gain.
In a next blog post we will investigate the implications of this result on the evolutionary dynamics of species locked in a competitive cycle. We will see that in such cases the expression 'survival of the fittest' acquires a counter-intuitive meaning.
-- Notes --
* This exercise also demonstrates that there is more to successful RPS play than being unpredictable. You can enter an RPS tournament knowing that random play can not be beaten, but that does not help you very much. Random play can not be beaten, but neither can it win. Random play is the strategy optimized for reaching a tie against any opponent, including the Nemesis. But one can not win a tournament with neutral scores. So the successful RPS player utilizes the fact that she is facing fallible humans and not the Nemesis. Therefore she deviates from the purely random strategy, and rather exploits the patterns she detects in the opponent's choices. In doing so, she obviously becomes predictable herself. But the opponent is unlikely going to spot the pattern she is exposing. The reason for that? The pattern that she follows is a (shifted) copy of her opponent's pattern. And the fact that the opponent is exposing that very pattern whilst he is trying to avoid being predictable, means he is blind to that pattern.
** A game is symmetric if both player have the same strategies (yielding the same pay-offs) available, and a game is a zero-sum game in case one player's loss is the other player's gain. Games like chess are zero-sum, but not fully symmetric: only one of both players can select the starting move.




Comments