Sometimes math has to create a story because real numbers don't work, even if the physics does.
Wave-particle duality, a foundation of quantum mechanics, has a fascinating science history. James Clerk Maxwell, whose equations govern the device you are reading this article on, couldn't explain everything - he died of cancer at age 46. It was left to Albert Einstein a generation later, in his 1905 paper, to describe light as photons containing properties of both particles and electromagnetic fields - the waves of Maxwell.
In 1923, Louis de Broglie came up with an idea for how particles could behave like waves and then two physicists at Western Electric, Lester Germer and Clinton Davisson, proved it with electrons. But there was still something missing from that physical proof - an explanation using using real numbers. I mentioned Maxwell's Equations being fundamental to the device you are this reading on, and they are the basis for a trillion-dollar industry, but despite that I wish you good luck defining a magnetic field without being recursive (like it's a field in the presence of a magnet). So it goes with wave-particle duality without using imaginary numbers. Real numbers are for measurable physical quantities. This has not really been an obstacle. Sometimes things work even if it's a bit of a black box how, so complex numbers have real and imaginary aspects; a and bi. a and b are real while i is imaginary.
A new paper says that rather than complex numbers being a purely mathematical invention to "facilitate calculations for physicists", quantum states and complex numbers are instead ironically and inextricably linked. They even can show it experimentally.
There is no i in the real world. You can have one pair of shoes, you can have two, and if the dog takes the left one you can have 1/2 of a pair of shoes but you can never have i pairs of shoes - shoes are not roots of negative numbers. Yet quantum mechanics deals with probability - if it will behave like a particle or a wave a la Schrödinger. Such changes in 'time' are called the wave function,and i is next to the wave function in Schrödinger's equation.
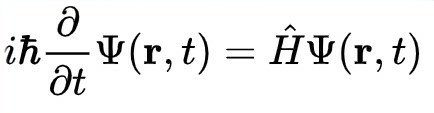
Complex numbers have an amplitude and phase and i describes the phase. Without it, the sum of all the probabilities can't be equal to one.
All fine for math, but you can see why the public thinks that is not real, any more than subject-verb agreement in a story is "real", even as it's important, or that adjectives need to go in a certain order - "size comes before colour, green great dragons can't exist" - in a story. Obviously such a thing can exist, English is not the only language and I am tempted to write a story in English using no adjective in commonly accepted order because I am a rebel. That is why complex numbers also have their place when the math is not middle school.
Scientists have debated whether or not the quantum realm can be shown with real numbers. That is what the new paper sought to answer, and they used our old friends Alice and Bob, from the seminal 1978 paper by Rivest and Adleman, when encryption was already a big concern.
If two photons are in one of two quantum states, you need complex numbers to tell them apart. Only then can you send one photon to Alice and the other to Bob where they can be measured and compared.
"Let's assume Alice and Bob's measurement results can only take on the values of 0 or 1. Alice sees a nonsensical sequence of 0s and 1s, as does Bob. However, if they communicate, they can establish links between the relevant measurements. If the game master sends them a correlated state, when one sees a result of 0, so will the other. If they receive an anti-correlated state, when Alice measures 0, Bob will have 1. By mutual agreement, Alice and Bob could distinguish our states, but only if their quantum nature was fundamentally complex," says co-author Dr. Alexander Streltsov from the University of Warsaw.
More importantly, if you value experimental physics over theoretical, is that they did an experiment using linear optics. It proved "that complex numbers are an integral, indelible part of quantum mechanics."

Credit: USTC
What does it all mean in a practical sense? Quantum superposition in the real world has been a pipe dream since I was young but that is because it is evolutionary in the real world unlike revolutionary in the theoretical. Yet the real world has to accept that some things will always be complex and proceed from there. This paper moves us along that path.




Comments