Does it cost money to be green, or can a company make greater profits by being green? Even a decade ago, most companies thought environmental sensitivity was too expensive an option, that it would render them uncompetitive in a harsh marketplace. Today, most thoughtful CEOs understand that environmentally sustainable products and practices are keys to greater profits.[1]

What happened? How did a short ten years change attitudes and practices?






  • New technologies made it easier to sort waste for resale, to burn fuel more cleanly, to use less energy, substitute safer chemicals for cloroflourocarbons, and so forth.





  • More customers decided they want green products and in some cases are willing to pay more for them.





  • New legislation tightened environmental regulations, making it harder to undercut competitors on price by polluting the environment.



Thirty years ago US manufacturers thought attention to product quality was a needless cost. Inspections, design for reliability, and other quality measures stood in the way of production rates, getting enough product out the door to satisfy voracious consumer demand. Then Phil Crosby[2] introduced the notion that “quality is free” – that companies save enough money through reduced product returns, reduced re-work, and better customer loyalty to offset the cost of quality. Finally, the triumph of Japanese cars in the American market showed that customers demanded quality even if it meant backing off from our deeply held “buy American” sentiment.

What changed? New technologies helped manufacturers build quality into the design and manufacturing processes, rather than simply inspect for quality at the end of an assembly line. The culture of conspicuous consumption and planned obsolescence passed, as consumers became more environmentally aware and demanding of safe, durable products. Baby boomers began to have their own children and developed a passion for serviceable, safe cribs and strollers. Ralph Nader blew the whistle on unsafe Corvairs; the Consumer Product Safety Commission banned flammable children’s clothing[3] and lead in household paints and gasoline. We became busier people, less inclined to spend our time at repair shops dealing with product defects.

Similarly, in more stable economic times when technology was changing more slowly – and these times are only twenty years behind us - efficiency was held up as the highest business virtue. But what about flexibility? Oh, flexibility is nice, the thinking went, but we don’t need much of it because the business environment is not throwing us any surprises, and besides, flexibility costs money. Flexibility means finding ways to reduce machine set-up time, cross-training personnel, diversifying the product line. Those costs would reduce efficiency.

Then came “mass customization,” the Internet, biotech, etc. The new corporate catch-phrase was “adapt or die[4] .” Robots now streamline materials handling and machine setup. “Human Resource” departments, formerly dissed within firms, become the most important corporate function in Silicon Valley enterprises; every firm now wants the most resilient, creative, diverse, and versatile workforce. Efficiency is still important, but flexibility is given co-equal status.

Profit and sustainability. Cost and quality. Efficiency and flexibility. In each instance, two variables were seen as trade-offs, and subsequent developments in technology, in social attitude and consumer taste, and in regulation, turned the tradeoff into a mutually-reinforcing relationship. Environmentalism, for example, formerly an irrecoverable cost, became profitable. We call this the transition from trade-off to mutuality.

This article presents a conceptual approach to modeling these transitions mathematically[5], and suggests developments which would make the approach practical. We develop the approach using the changing profit-environmentalism relationship as an example.

Suppose for example that y represents profit, x represents a sustainability score (the inverse of environmental impact), and y depends, in part, on a parameterized function of x which we will write as .

We look for a function  with the following characteristics:




  1. dy/dx < 0 when  is less than some critical value L.




  2. dy/dx > 0 when is greater than L.




  3. No value of may imply that y = 0.





Therefore let L=0, and let = .  Then for negative , has a negative slope; for example,  = 1/x; and contrariwise for positive , with  = x.

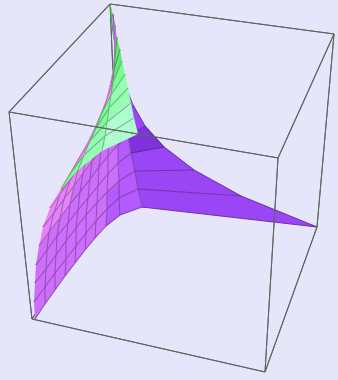
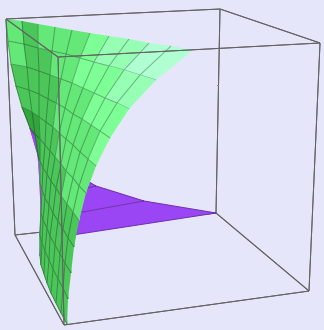
3-D surface views of the transition. The f and x axes are on the "floor" of the "room," and the lambda axis is the vertical. The graphs were made using Surface Grapher V 2.0, an html utility.

We cannot simply equate y with because = 0 would constrain y to unity,
nonsensical from an economic perspective. For realism, suppose there is a conventional production function g(u) defining the firm’s profit, in which the vector u does not include the greenness variable x. We now have


for which  when = 0 .[6]

When profit and greenness were seen as antithetical, would have taken on a negative value. When profit and greenness came to be seen as mutually reinforcing, became positive. Because this reasoning injects a time element to the discussion, we re-write as .

Modeling the transition becomes a task of estimating the time path of .

We can elaborate this to encompass the causal factors mentioned earlier in this article. Formally, replace the scalar parameter  with a vector , introduce a weighting vector v, and  becomes . 

As a practicality for modeling, let 

,

where is a measure of changing consumer taste, a measure of changing technology, a measure of changes in regulation and legislation, and each factor a, and obeys the rules (1-3) imposed earlier on the scalar .  a, b, and c weight these factors. The equation above is easily linearized:



Viewing y and x now as observed values, and adding an error term , the equation



may be used as a linear regression hypothesis by those who are not squeamish about appending the error term after the linear transformation rather than before. The regression estimate would be constrained by our wish to have  equal to zero at the moment of transition.

As with , and must be seen as time-varying, and once the regression equation is fitted, the task of modeling the transition is one of estimating the tracks of and versus t. This could be done through empirical observation followed by extrapolation, or by expert opinion survey. In either option, suitable data scales would have to be devised.

[1] An Amazon.com search turns up recent titles like Billion Dollar Green: Profit from the Eco Revolution, and Green Profit on Retailing.

[2] Philip B. Crosby, Quality Is Free. Mentor (1980).

[3] The whimsical among you are visualizing naked, flammable children. No, silly, I mean flammable clothing for children, which tragically had caused many deaths before becoming subject to federal regulation.

[4] Again from searching Amazon.com: Adapt or Die: Transforming Your Supply Chain into an Adaptive Business Network, by Bob Betts and Claus Heinrich, Wiley (2003).

[5] This part of the blog grew out of discussions with Prof. Dr. Eberhard Becker of Dortmund University of Technology.

[6] Setting  , which might be seen as even simpler choice, would satisfy conditions 1 and 2 above, but not condition 3 when we write . y would be forced to zero. In any case, the surface , where varies, say, from -1 to 1, is more mathematically interesting and might qualify as a “catastrophe” in the sense of Thom [Rene Thom, Structural Stability and Morphogenesis. Westview Press (1994)].