In a famous mathematical thought experiment, the goal is to make randomness deterministic by closed-form equation, so mathematicians tried to determine the path of a 'drunken sailor' staggering around a town. 

If there are street lamps, he will run into them, change his direction and keep moving until he gets out of the city. Logically, the time he spends in the area depends on the number of street lamps but the surprising answer is that the number of streetlamps are not the big factor.

First, look at the problem in simple form, using only a few exits, courtesy of the University of Athens:

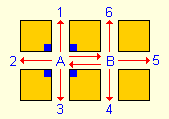
Probability for each one of the exits 1, 2, 3:
 

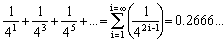
Probability for each one of the exits 4, 5, 6: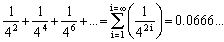

If the distance between our street lamps is large or small, a random walk will take the same amount of time. This 'dwell time' is a universal phenomenon, according to a paper it can be be observed in completely different systems - from crawling ants to light waves in disordered media.

Traveling Through Imperfect Materials

 Vienna University of Technology Professor Stefan Rotter's team analyzed the propagation of waves in disordered media, such as light waves in turbid glass or quantum particles moving as a quantum wave through a material with impurities.

"Usually, such transport phenomena are characterized by the so-called mean free path," says Stefan Rotter.

It is the length of the path a particle or a wave can typically travel freely until it hits the next obstacle.  In the case of the drunken sailor, the mean free path would be the average distance between the street lamps. In turbid glass, it would be the distance between two microscopic impurities at which the light wave is scattered.

The Length of the Path Stays the Same

Many important physical quantities depend on the mean free path - for instance the fraction of the light, which passes through semi-transparent glass.

"We can calculate how much time the transmitted part and the reflected part of the light wave spend inside the glass, respectively. These quantities, the transmission time and the reflection time, heavily depend on the mean free path," says Phillip Ambichl, PhD-student in Stefan Rotter's team and co-author of the paper. 

 Ants and waves -- are there similarities? Even in biology, this phenomenon can be observed: the path of ants crawling across a surface can be described as a random walk. A large ant will traverse an area with a smaller number of steps than a small ant that will change its direction more often. But regardless of their size, the time they spend on a given area is always the same. Credit: TU Wien / ant picture: Bild:Fir0002/Flagstaffotos, GNU Free Documentation Licence 1.2

But when those two quantities are combined to calculate the overall time the average particle or wave spends inside the medium, then the mean free path drops out of the result entirely. Quite surprisingly, light spends as much time in a turbid glass plate as in a transparent one.

It is the same with the drunken sailor: If his erratic path is blocked by an increasing number of street lamps, there is a higher probability of the sailor hitting one of lamps right at the beginning, so that he will turn around and never venture far into the square - the time he spends on the square would thus be reduced. If, however, he happens to enter deep into the forest of street lamps, he will be trapped there for a long time.

Paths leading to the opposite side of the square thus become much longer when the number of street lamps increases.

As it turns out these two opposing effects fully compensate each other, so that the total average dwell time remains the same when changing the number of street lamps.

"It is quite a surprise to see that this effect shows up in completely different systems", says Philipp Ambichl. "Our findings apply to rubber balls rolling across a wooden plank, hitting randomly distributed nails, as well as to electron waves traveling through a disordered system, in which the electron can be scattered at individual atoms."

Even in biology, this phenomenon can be observed: the path of ants crawling across a surface can be described as a random walk too. A large ant will traverse an area with a smaller number of steps than a small ant that will change its direction more often. But regardless of their size, the time they spend on a given area is always the same.

"With the average dwell time in an area or in a specific medium we have identified a quantity which is completely independent of the mean free path. This remarkable result will help us to better understand quite different transport phenomena appearing also in everyday applications such as in solar cells," says Stefan Rotter.

Whether it is particles, waves or ants - by studying one system, one can also learn much about others, even if at first glance they may seem completely unrelated.