Many people have heard of the Golden Ratio, a ratio that is the midpoint between asymmetry and symmetry - when "the whole is to the larger as the larger is to the smaller". In numerical terms, it is 1.618. 

Mark Barr used the Greek letter Φ (phi) to represent it and that has stuch. Because it is inherently pleasing to us, stairways, buildings, paper sizes and lots of other things use Φ in their designs. In music, the octave, fifth, and major and minor sixths are ratios of consecutive numbers of the Fibonacci sequence, making them the closest low integer ratios to the golden ratio.

It is in many places in nature, so we may think it is common, but patterns appearing on both the very large and very small scale are extremely rare. So it is a puzzle and a delight, or just a coincidence, that skin cells and fairy circles in the Namibian desert have a similar pattern.


Namibian fairy circles are large barren patches of earth ringed by short grass dotting the desert like craters on the moon or giant polka dots. No one knows how they form. Credit: OIST

Desert fairy circles are considered one of nature's greatest mysteries because no one knows how they form. Different from mushroom rings, these fairy circles are large barren patches of earth ringed by short grass dotting the desert like craters on the moon or big freckles. Several groups are racing to figure out this bizarre phenomenon. Prof. Robert Sinclair, who heads the Mathematical Biology Unit at Okinawa Institute of Science and Technology Graduate University (OIST), and collaborator Haozhe Zhang believe they have identified a small, but vital piece of the puzzle.

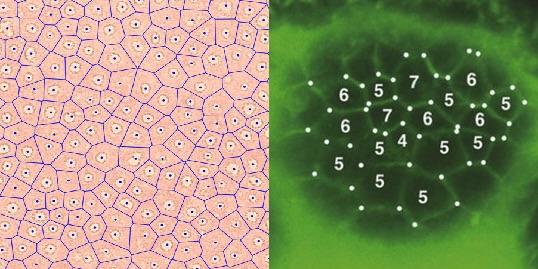
The distribution of fairy circles throughout the desert may look random, but turns out to have a pattern that very closely matches the distribution pattern of skin cells. A pattern spanning such drastically different size scales -- microscopic skin cells and the desert landscape -- is almost unheard of in nature.


Credit: OIST

"It is still difficult to say why exactly they are similar, but the fact that they are similar is already very important," Sinclair said. "This is suggesting there may be such types of patterns that cover really different size scales."

To conduct the analysis, Sinclair and Zhang compared the number of neighbors adjacent to fairy circles and skin cells. They took satellite images of fairy circles, and a computer drew lines halfway between each pair of circles to designate invisible boundaries, much like cell walls. The computer then counted how many neighbors surround each fairy circle. Other researchers had calculated skin cell neighbors several years ago.

The results were almost identical. Both the majority of fairy circles and majority of cells have six neighbors. But the similarity gets even more specific -- the percentage of fairy circles with four, five, six, seven, eight and nine neighbors is essentially the same as the skin cells.

"I didn't expect it to be so close," Sinclair said. "We spent a lot of time checking because it really looked too close to believe."

Many theories about how fairy circles form -- from rolling zebras to underground gases to dying trees -- have been proven incorrect. Now, some scientists are developing mathematical models attempting to explain the origin of fairy circles.


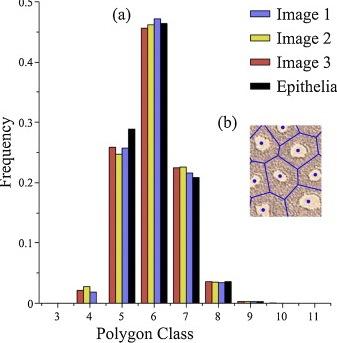
The distribution of Namibian fairy circles with four, five, six, seven, eight and nine neighbors is essentially the same as skin cells -- statistically indistinguishable. The patterns are so close, the researchers rechecked the data several times to ensure it was correct. Credit: OIST

"These models have to incorporate our results," said Zhang, a Ph.D. student in the Department of Statistics at Iowa State University, who conducted the research at OIST with Sinclair in 2013.

The researchers suspect the patterns might be similar because both skin cells and fairy circles are fighting for space. If true, scientists might one day be able to glean information about systems just by analyzing patterns. For example, they could search for signs of life on other planets or moons, where images are usually the only data initially available.

Finding such a pattern could also benefit ecology and biology in general. Understanding processes on one scale could illuminate what is happening at the other end of the spectrum. "Otherwise, we need a whole new theory for each type of system we study, and may miss general principles, or, as some say, not see the forest for the trees," Sinclair said.

 Published in Ecological Complexity.