Data on the distribution of wealth is apparently hard to come by directly, but inheritance tax data from the UK for some years is available. This data, it turns out, can be well-fit by an exponential function, over most of the UK population [1]. That is, the probability of having w amount of wealth appeared to be proportional to exp(-w/T), for some constant T. Income tax data from the US from 1983 through 2005 [1-5], the UK from 1994 through 1999 [1], and Australia from 1989 through 2000 [4] also followed an exponential curve.
It seems that poverty is most probable, while the likelihood of being rich exponentially vanishes with greater riches, for the vast majority of the population.
Because the distribution of money looks like it may be fairly robust across several different countries and years, and because that distribution is, to good approximation, simple in form, it seems reasonable to guess that the distribution emerges from some simple, universal principles. Of course there are myriad complications, such as government intervention, but some of these can be considered high-order corrections. For the purpose of understanding the leading order behavior, suppose we parsimoniously construct an agent-based model as follows.
Some constant number of individuals we will call agents periodically have financial transactions with each other, arranged by random pairing. A financial transaction, for now, is just a random exchange of money. This can be implemented in a number of ways; for example, each agent in a transaction may select a random number between 0 and 1, and then the agent with the smaller number will pay the other agent an amount proportional to the difference (if it can). Money is assumed to be conserved, which should be a valid assumption provided that money is exchanged at a rate sufficiently faster than that of inflation.
I coded up the above game rules and simulated 100000 agents for 1000 rounds of transactions. Each was initially given one unit of money. The figure shows my results: the probability "P($)" for having a certain amount of money, denoted $, plotted from my actual data and compared with the exponential function (wherein the "temperature" T is 1).
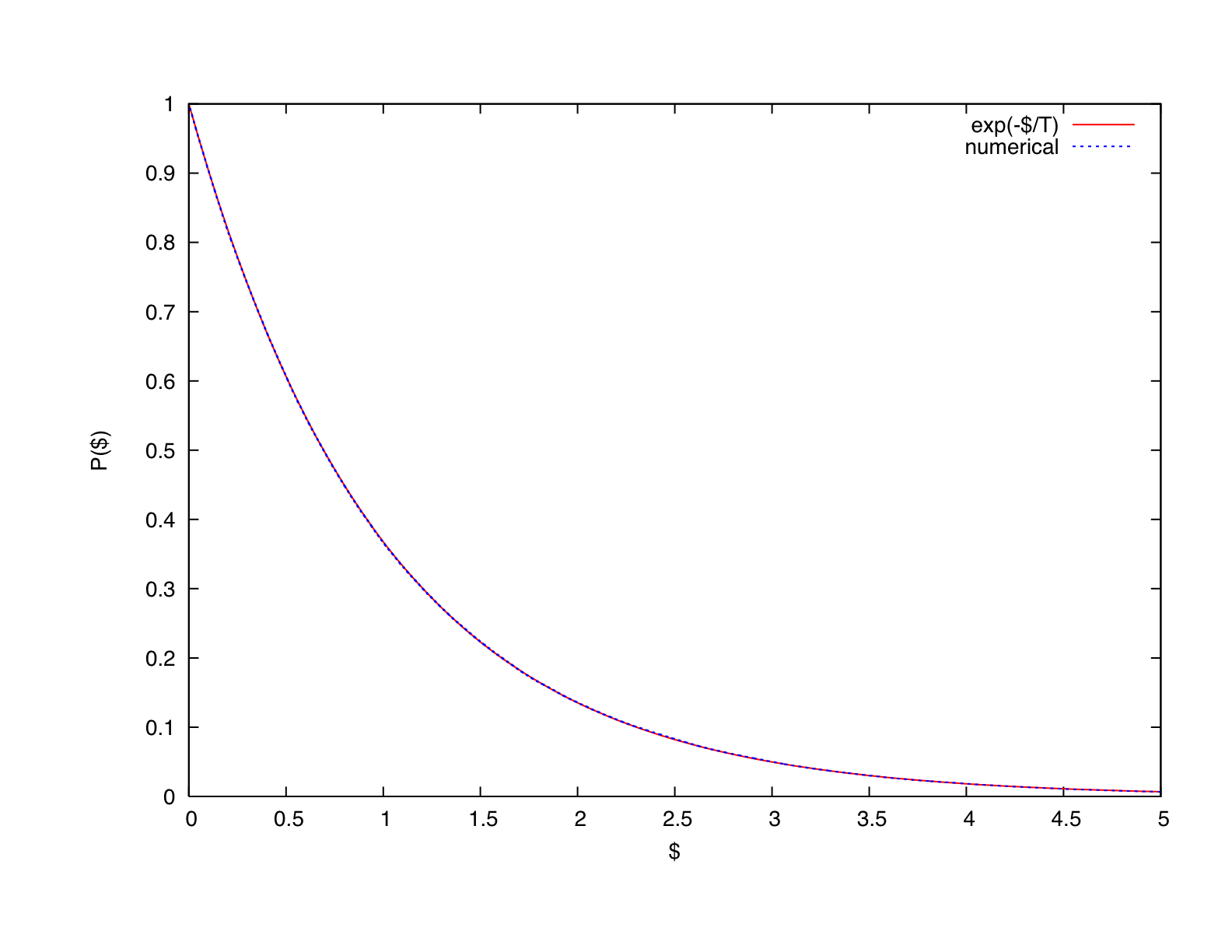
This model is analogous to the Boltzmann-Gibbs statistics for particles in a gas. Agents are analogous to particles, transactions to collisions, money to energy, the average money per agent to temperature. The probability that a particle of gas with temperature T has energy E is proportional to exp(-E/T). Among the first to apply this analogy to the distribution of wealth and income were Victor Yakovenko, professor of physics at the University of Maryland, and his student Adrian Dragulesku. [6].
As in the model above, they randomly paired each agent with any of the other agents, for each transaction. Then they effectively "flipped a coin" to determine the payer and payee. They tried various formulas for the payment, including: a constant amount, a random fraction of a constant amount, and a random fraction of the average money of the pair. In the case of income, they suggest the pair-wise transactions can be associated with equally qualified candidates competing for positions. They also simulated a somewhat more sophisticated model in which agents can start up firms, borrow money, hire other agents, and produce and sell products. Alternatively Victor Yakovenko with Barkley Rosser, professor of economics at James Madison University, considered a model in which agents individually interact with a large reservoir of money, e.g. a company, instead of directly with each other [4]. All of these variants resulted in the same distribution.
For both wealth and income, Dragulesku, Yakavenko, and collaborators predict that the probability of having x wealth or x income is exp(-x/T)/T. The fits subsequently made to the data mentioned above are impressive considering there was only one fitting parameter, T.
This does not constitute definitive proof that the approach of this type of model is valid. But assuming the possibility, it is interesting to consider implications.
Although the exponential shape of the resulting distribution is very stable, each individual agent is free, in these models, to move up and down the curve. The speed of economic mobility is restricted only by the amount of money that can be exchanged in one transaction. But perhaps in some circumstances it is more realistic if, instead of randomly pairing with anybody, agents are further limited to dealing only with other agents of similar economic status. I've found that if the difference in finances between paired agents is restricted to be less than some constant, then there is still no significant departure from the eventual exponential distribution (although individual economic mobility is further slowed).
Then there is the curious variation in ability among these modeled agents (assuming some measure of the ability to earn money or make intelligent financial decisions). What is so curious about it, like the incident of the dog in the night time [7], is its absence. We have implicitly assumed that all agents are equally capable, which is why success or failure is determined by chance.
One way to model ability is with a one-dimensional parameter that biases the otherwise random financial outcomes. The simplest type of bias is linear. Suppose each agent has an ability quotient, AQ, between 0 and some maximum possible score MAXAQ, where MAXAQ is less than 1. Recall that in my original model above the financial success of each agent was determined by a random number between 0 and 1. Replace this purely random number with the sum of AQ and a random number between 1-MAXAQ and 1.
Now, what determines the AQ of each agent? It can either be innate or acquired. If innate, then each agent is born with an AQ that is constant throughout its simulated lifetime. If acquired, then the AQ of each agent varies dynamically, presumably with financial status. In either case, we need a specific prescription for distributing ability among the agents. There are many ways this can be done.
I tried the following. In the case of innate ability, the AQ was uniformly distributed between 0 and MAXAQ. In the case of acquired ability, the AQ of each agent was set equal the ratio of that agent's money with that of the richest agent. I then ran tests, for thousands of iterations, of both cases, for various values of MAXAQ. Noting that MAXAQ represents the fraction that ability, as opposed to chance, determines the outcome of a transaction, I found that a 10% contribution from either type of ability results in more than a 10% departure from an exponential, over most of the financial range. It seems that, within the framework of this type of agent-based model, ability must be fairly equitably distributed in order to fit the data.
In explaining the applicability of equal-ability, agent-based models to the real world, economicist Ian Wright argued that the large scale economy is so dynamic, and the range of situations presented to each individual so large, that the resulting unpredictability of financial dealings is well-modeled by randomness [8]. He pointed out that statistical mechanics similarly oversimplify molecular dynamics, yet accurately predict the macroscopic properties of gases. Masanao Aoki, professor of economics at UCLA, offered similar justification for financial unpredictability lending itself to stochastic modeling, noting that the environment local to each individual is unique and subject to "idiosyncratic shocks" [9].
The suggestion here is ultimately an optimistic one. The observed disparity in money does not necessarily imply commensurate disparity in ability.
[1] A. Dragulescu, V. Yakovenko, Physica A 299, 213 (2001). arXiv:0905.1518v1
[2] A. Dragulescu, V. Yakovenko, European Physical Journal B 20, 585 (2001). arXiv:cond-mat/0008305v2
[3] A. Silva, V. Yakovenko, Europhys. Lett. 69, 304 (2005). arXiv:cond-mat/0406385v3
[4] V. Yakovenko, J. Rosser (2009). arXiv:0905.1518v1
[5] A. Banerjee, V. Yakovenko, T. Di Matteo, Physica A 370, 54 (2006). arXiv:physics/0601176v1
[6] A. Dragulescu, V. Yakovenko, Eur. Phys. J. B 17, 723 (2000). arXiv:cond-mat/0001432v4
[7] Sir Arthur Conan Doyle, The Memoirs of Sherlock Holmes, George Newnes, United Kingdom (1894).
[8] I. Wright, Economics E-journal Discussion Paper 2008-41 (2008). http://www.economics-ejournal.org/economics/discussionpapers/2008-41
[9] M. Aoki, Modeling aggregate behavior and fluctuations in economics, Cambridge University Press, Cambridge (2002).
The Bolzmann-Gibbs analysis is a keen one, I think, though I can accept that the ability quotient won't behave as nicely as math would like so that might skew the results. Still, there has to be a pretty good game engine in there. Companies have made billions using 2 body dynamics for action so something a little more complex for strategy games would be a hit. I'm probably not the first person to think of it but, if I am, let's keep it to ourselves.