One of the cool things I have learned to do, through years of experience in data analysis at particle colliders, is to visualize the complex kinematics of a signal process in a multi-dimensional space, and imagine ways to separate it from backgrounds by selecting in the hyperspace the signal-rich region. I came across a very simple example of the above rather abstract statement yesterday, and I wish to share it with you.

To help you visualize what I am going to discuss, here is the example: an avocado in a square tumbler. The avocado is top pair production, and the glass is Z plus b-antib production.
... Confused ? Let me explain.
Imagine you want to measure
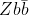
production at the LHC.
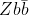
production is a process which is a background to several searches for new physics, and which we do not know with very good accuracy from theoretical predictions -it has never been measured very precisely. Now,
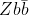
events can be collected by selecting collisions yielding two high-energy leptons making the Z mass, plus two b-quark jets. Unfortunately, top pair production may produce exactly the same signature, when both W bosons in the decay chain
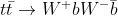
end up producing charged lepton-neutrino pairs, as in
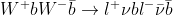
.
If we compare the above final state with the one arising from
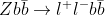
, we notice that top pairs are indeed a nagging background to our
signal: there are many features capable of distinguishing the two processes, but these need to be extracted from the different kinematics, and not simply by the leptons and jets measured in the event.
The most striking thing telling apart
and
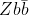
is the presence of two energetic neutrinos in the final state of the former. Thus, it seems that the best thing to do is to require that the event possesses little missing transverse energy (
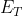
): missing energy is a signature of the escape of energetic neutrinos, but at a hadron collider only the component transverse to the beam can be measured meaningfully. The magnitude of missing
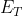
is thus the first "dimension" in the multidimensional space we wish to consider, to separate
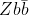
and top pairs.
Now, apart from neutrino escape, missing transverse energy may originate from another process: an underestimate or overestimate of the energy of a jet. If one of the two b-jets originating from b-quark hadronization gets heavily undermeasured, for instance, there will be missing energy in the event, even in the absence of neutrinos. This missing energy will be aligned with the jet direction. If, on the other hand, the jet energy is overestimated, the missing energy may be pointing in the direction opposite to that jet.
We have two jets in the final state, so in the simplest case, a
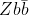
event may produce significant missing transverse energy most likely if the latter points along one of the two jets, or opposite to it. On the other hand, top pair events will have the neutrinos leaving in any direction, and the angle between missing energy and the two jets will have any value: there will be, in general, no alignment between missing Et and the jets.
The two other directions in our "discriminating space" are thus the angles between missing
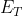
and each of the two observed jets. Each angle may take any value in the interval 0-3.14, but we know that for a
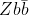
event most likely either of the two angles will be close to 0 or close to 3.14.
Now try to figure out the three-dimensional space of the two angles I just described, and the magnitude of the missing
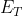
vector (notice that I am specifically not adding more figures to this article, to force you to think hard without any visual aid). The plane spanned by the two angles is well-represented by the bottom of the glass in the picture above, while the vertical extension of the glass is along the direction where missing
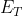
increases.
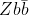
events will most likely populate the region occupied by the glass! In fact, for low missing
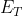
, this will have any angle -it is unsignificant, so it is not necessarily aligned with a jet. This constitutes the thick bottom of the glass. But for larger missing
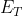
(above the bottom), the glass only distributes on the edges of the square spanned by the two angles: that is because a large missing
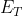
will most likely be aligned or anti-aligned with either of the two jets!
Now take top pairs: the missing
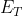
vector is larger for them, because these events have indeed produced two energetic neutrinos. But in general, there will be little or no correlation between the missing
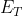
vector (which is the vector sum of the two neutrino momenta) and the jet directions. So the missing
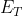
will populate uniformly the plane of the two angles. Top pair production can thus be well visualized as the fruit inside the glass, lying above the thick glass bottom.
If you can visualize these three variables for the two physical processes, it will become easy for you to formulate a strategy to remove the top-pair background from the data, retaining only the
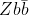
events you want to measure: you select events that either have low missing
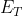
, or have larger missing
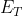
provided it is aligned with one of the two jets. You thus "carve" the glass out of the fruit.
Of course I have discussed the matter without having looked beforehand at a Monte Carlo simulation of the two processes. If I constructed a graph of the missing
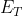
and the angles, I might end up discovering that my idealized discrimination works less well than I naively pictured in my mind. Nevertheless, the capability of visualizing multiple dimensions is a very important tool in the search of subnuclear physics signals.
 To help you visualize what I am going to discuss, here is the example: an avocado in a square tumbler. The avocado is top pair production, and the glass is Z plus b-antib production.
To help you visualize what I am going to discuss, here is the example: an avocado in a square tumbler. The avocado is top pair production, and the glass is Z plus b-antib production. 



Comments