In short particles with more mass lead to beams with more energy. More massive particles reach these energies
with much smaller machines. Interesting and fundamental physics
would be possible with a muon collider, of 6.3 km circumference and
neutrino factory which would be far less expensive than a 50 km
linear electron accelerator. As we learned from the Superconducting Supercollider less expensive is good, more expensive is less likely to be built
Image of one of the buildings for the superconducting supercollider credit wikimedia.
Scientific minds like equations. Think of it this way. A fundamental law of accelerator design and construction.
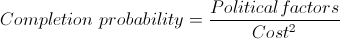
The cost of an accelerator is proportional to the kilometers of tunnel that need to be dug.
Many people know of the International
Linear Collider proposed as a next generation machine which could
breath new life into Fermilab or found a new center for particle
physics at another location. In terms of the physics which such a facility could perform no one will dispute it's value to mankind. However, in terms of politics and economics the digging of 50 km of tunnel to build such a device may not be politically viable. For that reason alone it is wise to be aware of, and to pursue alternatives. This is the lesson everyone of a certain age should remember from the Superconducting Supercollider and the LHC. At one point the LHC was the alternative, red headed step child to follow on to the Supercollider. Now look at it.
Not as many people know about the
research efforts directed towards a muon collider / neutrino factory.
This alternative to a linear accelerator would be far less
expensive to construct. The full details are here (
http://map.fnal.gov/muon-collider/why-muons.shtml
) this blog will explain for a general audience why a muon collider
is a good option. To see why a muon collider and it's
more massive particles provide a more economical alternative, let us
forget about fancy greek words and think about Einstein's old formula
E= Mc^2 in the way a high school student would. Back in 1997 I
wrote it in a question to Fermilab. Which I was honored, a while after I wrote it and exchanged emails, to have my question and an answer posted on their website.
Accelerate a Gram of Matter
Dear: To Whom This May Concern
I know that the Tevatron can accelerate a particle up to one TeV. Can it accelerate a larger mass. If so I have an exparament you might be interested in. This exparament is comparable to what the half built Super Conducting Super Collider was meant for.
Take a look at this equation and see if it means anything to you:
C^2 M = E for instance 186,453 m s^-1 / 1 Gram = 34.527 GeV.
I think the reason why you need to build such large accelerators is because your accelerating individual subatomic particles. When you should be accel erating larger masses like one or two grams. The result of this experiment would be the following:
- The matter being accelerated would decay directly into radiant energy the instant it reached the speed of light.
- The instant it slowed down the radiant energy would just radiate away in the form of microwaves. Or form up into matter.
I'm sure that the 20 ton magnets that the Tevatron is made of have the power to do that. I would greatly appreciate it if you would give me some feed back on this.
Sincerely, Hontas F. Farmer
As you can see in 1997 I probably had
many wrong ideas. (I didn't even know to represent an exponent using ^n. ) Chief among them is that it's a totally
impractical idea to do this with a gram of matter. Such a large mass of matter would lack a
fundamental electric charge. Charging it up with static would result
in those charges being ripped off the surface of the mass. The total
energy of each fundamental collision of two such masses would be
divided by the number of fundamental particles in the mass. It seems that I forgot to square c. Mostly things that I as a high school student of about 16 going on 17 years old would
not have known to check. I don't think I had even taken non-calculus based high school physics yet, so go easy on me for that.
Never the less, the basic idea is
correct. It works because the well known formula E=Mc^2 isn't the
whole story. There is a factor which is
always left out of the popular version. E= \gamma Mc^2.
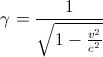
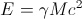
That extra
term is where many of the interesting aspects of special relativity
lay. One of those is the faster a particle moves, for a constant
mass, the more energy it has. So I thought to myself, and so have
many others before and since, why not accelerate a more massive
particle to get higher energy particle beams? The problem is that
fundamental particles heavier than electrons or protons are generally
not stable. There are ways of overcoming this.
There are many interesting
possibilities raised by this line of research. Such as the
possibility of a neutrino collider as a side project. A neutrino collider would have the problem of a low number of
events because neutrinos hardly ever interact with anything. However
those few events could teach us about the origins of neutrino masses.
Neutrino masses are not predicted by the standard model of particle
physics, the best most well tested model in all of physics, assumes
them to be massless. This is a really big mystery and hints at new
physics.
All of the above interesting and
fundamental physics would be possible with a muon collider and
neutrino factory which would be far less expensive than a 50 km linear
accelerator. A massive linac would have certain advantages but it's
great disadvantage, cost, may make it politically radioactive. Let us
not forget the lesson of the Superconducting Supercolider. The physics community as a whole needs to remember to support alternatives like a Muon collider, not just in research those on the inside know of, but in public outreach as well.
