H⁰ charge "clouds" in |4,3,1> state.

       

In about 1985, while considering a banal problem of scattering from atoms, I occasionally discovered the positive-charge (second) atomic form-factors

                                           

describing effects of interaction of a charged projectile with the atomic nucleus [1]:

(1)

(2)

(3)

To my surprise, it was unknown and it was absent in textbooks despite easiness of its derivation and a transparent physical sense. Namely, for elastic scattering f_nⁿ(q) describes the positive charge distribution in an atom and for inelastic processes n-->n' the form-factors f_n^n'(q) describe the excitation amplitudes due to transmitting an essential momentum q to the nucleus while scattering. In Fig. 1 one can see 2D plots of the atomic wave functions describing the relative electron-nucleus motion in the Hydrogen atom or a Hydrogen-like ion. Strictly speaking, they are the relative distance probabilities although they are often erroneously called “negative charge clouds”:

Fig. 1. Probability density 2D cuts (electron-nucleus relative distance probability).

I say "erroneously" because quite similar, “positive charge clouds”, exist at much shorter distances due to nucleus motion around atomic center of inertia (CI). The nucleus does not stay at the atomic CI but moves around it. So the charge density pictures include the positive clouds too. This fact follows from formulas (1-3): both charge clouds are expressed via the same atomic wave function .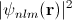

Fig. 2 represents qualitatively such a picture for a particular state of a Hydrogen-like ion. (See also a more complicated header picture for |4,3,1>.)

                                 

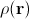Fig. 2. Qualitative image of atomic charge density 2D plot  for the state |3,2,2>.

If we make a zoom in, we will see a picture similar to Fig. 1 since f(q) 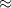F((m_e/M_A)q). Two dots in the middle are "positive charge clouds". In other words, Fig. 1, without scale indicated in it, describes charge density projections of a Hydrogen-like ion at “atomic” distances (for negative charge) equally well as it does at “short” distances for positive charge. This is the true, elastic physics of short distances. Unexpected?

I do not want to discuss here a provocative fact that each “sub-cloud” contains a fractional charge ;-)  
I would like to underline that the nucleus is not seen as a point-like in elastic processes. It is quantum-mechanically smeared. And the most surprising thing about it is the smear size dependence on the electron configuration. The farther electron “orbit”, the larger the positive cloud. It looks counter-intuitively first but it is so! The atomic form-factors (2) and (3) are just the Fourier images of the cloud densities. The corresponding elastic cross section (1) can be written also via an effective projectile-atomic potential which is softer than the Coulomb
“singularity” at short distances [1].

By the way, in a solid state the positive charge “clouds” are rather large and comparable with the lattice step. Smearing is always the case for bound states.

In scattering experiments, however, it is extremely difficult to observe the true elastic events. Normally it is impossible to distinguish an elastically scattered projectile from inelastically scattered one. And normally nobody cares about the target atom final states (excited or not). So experimentally, when all scattered projectiles are only counted, one observes an inclusive cross section. It is the inclusive cross section of scattering at large angles



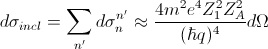
which is reduced to the Rutherford formula, as if the target atom were a point-like Coulomb center!

Similarly, the "free electron" in QED is not really free but is always coupled to the quantized electromagnetic field. So its charge is also smeared quantum-mechanically in an elastic picture.

This explains what elastic physics occurs at short distances: there is no Coulomb singularity, as a matter of fact.

[1] V. Kalitvianski, Atom as a “Dressed” Nucleus, CEJP, V. 7, N. 1, pp. 1-11 (2009), http://arxiv.org/abs/0806.2635 .