Lisa Pratt, the new planetary protection officer for NASA takes up her job at a challenging time for astrobiology. We are approaching a major decision point for Mars. If Elon Musk succeeds in his ambitious plans, then some time in the next couple of decades we may introduce trillions of hardy microbial spores to the planet. Not deliberately, but just because we can't help but take them with us wherever we go. This is a major quandary for astrobiology. But not just for astrobiologists.
I think almost anyone would be saddened if we had this headline news story in the 2030s:
Future Possible News : Mars Life Found Then Lost: Robert Walker:
Astronauts from Elon Musk's new "Mars Port" .0have just found native life there. It was in a sample from a damp streak on a steep slope near the city. They added it to nutrients and saw small cells swimming before their eyes. They analysed the sample and found that there was no DNA present. There were no proteins either. Just RNA fragments.
Sadly when they took another sample, they found DNA and proteins and evidence of Earth life. The life in their original sample has not survived, and so the video footage they took of those swimming cells is the only evidence we have that RNA world life ever was there.
Made with this spoof news story generator
First, some wonder why they should care about microbes, even extraterrestrial microbes. Well, it could be far sadder than you might imagine or guess, to lose such a discovery
This article is over 50 pages. It has a fair bit of duplication of content from some of my other articles, for instance explaining how harsh conditions are on Mars, expense of space suits, about Moon as a backup, how Mars can't be terraformed easily as in Kim Stanley Robinson's book, etc, because I found that I got asked all these things by comments on the article in Facebook.
- For a shorter version with the central points see Let's Make Sure Astronauts Won't Extinguish Native Mars Life - Op Ed - Shorter
WHY EXTRA TERRESTRIAL MICROBES WOULD BE SO AWESOME TO FIND
The interior of a cell is so complex, a million complex chemicals in an intricate dance, that to a microbiologist it resembles all the creatures in the web of life of an ecosystem. It's as if the only ecosystem you ever knew was the African savannah - every cell has a savannah landscape inside with its grass, lions and antelopes - and for the first time you find one that has a coral reef inside, with algae, fish, corals and octopuses. It could be as amazing as that to discover an extraterrestrial microbe based on a different biology.
They could be revolutionary in more prosaic ways too. For instance enzymes from microbes adapted to extreme cold are the basis for detergents that let you clean things just as thoroughly with cold water as you did previously with hot water, saving on power, and reducing CO2 emissions. Those enzymes form a $1 billion industry - and there are many other applications of extremophile enzymes. If we find a novel biology on Mars based on completely new principles, it could potentially be far more of an advance than that. The new insights, chemistry and biology could have countless applications in fields diverse, perhaps, as medicine, agriculture, nanotechnology, and a wide range of industries (more on this later)..
We are talking about a collision of distinct planetary biospheres here, that may have had little contact, or even none, since the origins of the solar system, especially in the Earth to Mars direction, as we'll see. This has never happened before and astrobiologists find it hard to predict what would happen. I like this example of RNA world cells, as it is one of the clearest you can make to show how vulnerable Mars life could be to our microbes.
We just don't know what would happen. But almost any scenario which leads to Earth microbes spreading through Mars habitats is likely to confuse our study of Mars, and our understanding of the planet and any biology there.
EMERGING EVIDENCE FOR MANY POTENTIAL HABITATS ON MARS IN THE LAST DECADE
Most astronauts would have said this was not much of an issue a decade ago as the surface of Mars appeared to be totally sterile to Earth life. This started to change around 2008 when Phoenix first found what appeared to be droplets of a liquid forming on its legs. Sadly it had no way to analyse them. They are now thought to have formed where salt and ice meet, thrown up after its landing. It also made isotopic measurements of the atmosphere which showed that there is a fair bit of water close enough to the surface to exchange oxygen atoms with the CO2 in the atmosphere, though it couldn't tell if this happens continuously or episodically.
Since then we have many ideas for habitats on Mars, as well as indirect evidence. They are most of them hidden below the surface and consist of only a thin film or droplet of brine - but a small droplet is a "swimming pool for a microbe" as Nilton Renno put it (who runs the Curiosity REMS weather station on Mars).
TAKEN AS A GIVEN BY MANY THAT HUMANS WOULD INTRODUCE EARTH MICROBES TO MARS IRREVERSIBLY
So how can we make sure this and other similarly sad Future Possible News stories won't happen?
Most of those writing on this subject today take as a given that humans are going to introduce Earth microbes to Mars. They say that what we have to do is to try to explore Mars by using robots as much as possible, and learn as much as we can in the brief window of time before the humans get there.
So far our rovers going to Mars have been sterilized to a high standard, but they haven't aimed for 100% sterile for practical reasons; it's just too hard to do . There are sure to be a few remaining hardy microbes sitting on them. However, the conditions there are harsh, and most think our microbes are dormant, just sitting there doing nothing, and that we haven't irreversibly introduced Earth microbes to Mars yet. Astrobiologists think that the planet is probably, so far, still in a state where we can explore it and find out about the native Mars biology, whatever it is, without the signal of Earth microbes to confuse our searches.
SUGGESTION OF RAPID EXPLORATION WITH "DIRTY ROBOTS" AND RELAX THE RULES
The astrobiologists Alberto Fairén and Dirk Schulze-Makuch aim to try to speed up the process of searching for life on Mars by relaxing the measures used to protect Mars from Earth life carried there on rovers. That may seem rather paradoxical, but they have argued, in the article "Searching for Life on Mars Before It Is Too Late" that after a human landing on the planet, it will already be irreversibly contaminated by Earth microbes, and that if we don't relax requirements now, we won't be able to search for native life on Mars at all before it is too late, saying:
"It is very likely that our children or grandchildren (the Mars generation) will see astronaut footprints on the red sands of Mars, and at that moment, it will be much too late to straightforwardly identify the nature of true indigenous martians."
So, for instance they wish to send Curiosity to investigate a possible wet streak close to where it is exploring, right now, before it is too late to study such streaks in their original state. They know that it is not sterilized enough, and might introduce Earth life to the streak, if it is habitable. However, they say that we don't have much time left to explore such places before it's too late - because after the first astronaut footprints in the Mars dust there will be Earth microbes already spreading throughout Mars.
(Microbial spores can get blown in the dust storms which sometimes become global, covering the entire planet -and also transporting dust between the two hemispheres as well, and at times so thick they turn day to night on the surface, blocking out the UV radiation that normally helps to sterilize spores in wind blown dust, also the iron oxides in the dust will naturally shield a spore imbedded in a crack in the dust).
The problem here is that our modern landers are not as easy to sterilize by baking them in an oven like the two Viking landers because modern instruments tend to be more heat sensitive than they were back then. This will make it more expensive, and by the time we have done it, they think our window of opportunity for studying the life will be over. Much of their paper is devoted to a discussion of ways to distinguish between habitats that are colonized by introduced Earth life from ones that still have only Mars life in them.
CURRENT PRACTICE - TO CONTINUE STERILIZING OUR ROVERS AS WE HAVE ENOUGH TIME TO DO THE SCIENCE PROPERLY BEFORE HUMANS GET THERE
The previous planetary protection officer Cassie Conley and the one before her, Jim Rummel, have strongly criticized this approach. They say that the proposed "dirty robots" would be as much of a problem as "dirty humans". They don't think the proposed methods to distinguish Earth from Mars life using genetic tests will be reliable.
They raise the point that we have had plans for humans to Mars as a near future mission for decades now, with nothing happening, and that the private spaceflight plans are "more hopeful than convincing", and that the future of both astrobiology and human missions depends on doing good science right now. They argue that there is still time to explore Mars properly before humans get there, and that it helps nobody to relax the requirements before we know what is there, saying:
A human mission to Mars is NASA's stated “horizon goal,” but this is not the same as a serious programmatic commitment—with an accepted rationale, budget, and schedule. To date, no government agency has produced such a commitment, and the details of private initiatives are still more hopeful than convincing. There is still time to explore Mars properly.
Their response is in their article "Four Fallacies and an Oversight: Searching for Mars Life,". The two papers are summarized in Debate Over Mars Exploration Strategy Heats Up in Astrobiology Journal, and both are open to read free online. I will discuss some of the other points made in these papers in more detail later on, so those short summaries just touch on some of the points they make.
Both are agreed on the central point however, that humans will introduce Earth microbes irreversibly to Mars, and that our best opportunity for studying any native life on Mars occurs before our Earth microbes are introduced to the planet. They differ in their views on how soon this may happen with the planetary protection officers suggesting it won't be for some time and that we have time to explore Mars properly.
WHAT IS LISA PRATT'S VIEW ON THIS - THE NEW PLANETARY PROTECTION OFFICER?
Cassie Conley has just been succeeded by Lisa Pratt as NASA's new planetary protection officer. The few statements she has made in her interviews with the press are already being interpreted as suggesting she is open to relaxing the rules for planetary protection, perhaps along the lines of permitting "dirty robots". I think it is far too soon to say such a thing, when she has just started on her new job, and anyway, it's not really for her to make such a decision. It has to be done at a higher level, in COSPAR.
I'm using the report from ScienceMag
First she says the same as everyone, that as soon as we've got humans there, we've lost the chance to study pristine Mars
“No matter what we do, the minute we’ve got humans in the area we’ve got a less pristine, less clean state,” Pratt said at the meeting. “Let’s hope we know before the humans get there, one way or the other, if there is an ecosystem at or near the surface.”
One of her remarks as reported in ScienceMag does seem to suggest that she supports "dirty robots"
How do we designate a few, a very small number, but a few special places on Mars [where] we can get in now with rovers and landers and do a better job asking and addressing questions of—is there present-day near-surface life on Mars? We can’t just declare every interesting place off the table. Because that means the first time we’ll know anything is when we’ve got humans there.”
That "We can’t just declare every interesting place off the table" does sound a bit like a suggestion for "dirty robots" .
However, John Rummel, a previous planetary protection officer, before Cassie Conley and then Lisa Pratt says
...John Rummel, a biologist at the SETI Institute in Champlain, New York, who led the protection office before Conley. “I would advocate for noncontamination of special regions, of course,” Rummel says. He also suggests that Pratt learn a bit more about the cleanliness standards before mulling any changes. “She is pretty careful, but still new to the job,”
Alberto Fairén, author of the "dirty robots" paper interprets what she said as supporting his proposal.
...Alberto Fairén, a planetary scientist at Cornell University who last year called for reducing cleanliness requirements in potential special regions and drew a sharp rebuke from Conley and Rummel. “It is really nice hearing that the new [planetary protection officer] starts her tenure with NASA announcing what can only be interpreted as the inception of a very interesting and most needed change in the Mars planetary protection philosophy thus far,”
Lisa Pratt's main point is that she wants to do it in a way that they assist missions, and don't look like some kind of a sheriff's department constantly coming down on them.
...But the office will also develop modern techniques for assessing microbial burdens, and it will seek a less confrontational relationship with the NASA centers, Pratt added. “We have to do it in a way that we assist the missions and don’t look like we’re some kind of sheriff’s department that is constantly coming down.”
NASA planetary protection officer suggests loosening limits on exploring Mars for life
LOOKING AT THE DEBATE AND ITS BASIC ASSUMPTION
I'm going to look at some of the challenges of her new job. And I will also look at this debate between astrobiologists, and I will talk over why the story in the Future Possible News that I just shared is a realistic example of something that could happen in our future.
I will also look at the basic assumption nearly everyone in this discussion makes, even the planetary protection officers - that as soon as we have the capability to land human "boots on Mars" that we will and should do it. Is that true. What are the alternatives?
Some would say that we are the biosphere's way of getting into space. If so, we are also the biosphere's "noosphere" to use Theillard de Chardin's word. Its way of thinking about the future, weighing up consequences, and protecting itself from things that could go wrong. That's us, ain't nobody else to do it for us.
Perhaps if you look at the alternatives to rushing astronaut's boots to the Mars surface, to make footprints in the dust as soon as we have the capability, you might start to like them.
It is worth looking at least, to see what those alternative futures might be like.
How to read this off-line
This article runs to about 50 printed pages (not including the images - word count over 23,000). If you want to read it offline:
- You can use Pocket - an application that helps with off line reading of web pages.
- You can also save this page as a pdf. On windows you can use print (Ctrl + P) then change the printer to the pdf printer. The Print button then changes into a Save button and you can then save it where you want.
Note: the embedded YouTube videos won't work if saved as a pdf, but for this page I've added "(Click to watch on YouTube)" links below each one and those will work in the pdf.
- You can also save it as a web page. Most web browsers have an option to save a page as "Web page complete" which includes all the images in the page saved on your computer for offline browsing. Be sure to give it time to download the page before you close the browser tab.
- I plan to make it available on kindle soon.
You can use the same methods for any of my longer articles here.
RELAXING PLANETARY PROTECTION RULES IS "ABOVE THE PAYGRADE" OF A PLANETARY PROTECTION OFFICER
Cassie Conley used to say in her interviews that decisions like that, about what precautions we have to take to protect other planets and Earth, are above her paygrade. It's the same for Lisa Pratt or any planetary protection officer. She couldn't make any promises about relaxing the rules anyway.
Our planetary protection requirements fall under the Outer Space Treaty, and in particular,
"Article IX: ... States Parties to the Treaty shall pursue studies of outer space, including the Moon and other celestial bodies, and conduct exploration of them so as to avoid their harmful contamination and also adverse changes in the environment of the Earth resulting from the introduction of extraterrestrial matter and, where necessary, shall adopt appropriate measures for this purpose ...
The guidelines on how to interpret this article are decided by an international group of astrobiologists through the COSPAR meetings, which are held every two years. She can't set the COSPAR policy herself. The planetary protection officer is only responsible for implementing it. She would be there when the decisions are made and she might have some input into the conversations but she would not make that decision.
TESLA ROADSTER DIDN'T HAVE A PLANETARY PROTECTION PLAN
Indeed if you listened carefully she showed her concern about the need to make sure that private space are on board with planetary protection provisions. I was surprised to hear from her interview that there was no planetary protection plan for the cherry red Tesla Roadster. As reported in SpaceNews:
Pratt said her office is also interested in working with potential commercial missions to Mars and other worlds subject to planetary protection protocols. Such discussions, she said, were limited prior to the Feb. 6 launch of a SpaceX Falcon Heavy rocket carrying a Tesla Roadster sports car into a heliocentric orbit that goes beyond the orbit of Mars.
Her office received many questions about NASA’s role in planetary protection for that mission, she said. “The answer was little or nothing,” she said. “We were supporting their launch, but we did not have a planetary protection plan in place.”
She called for more collaboration with commercial ventures on the issue, and suggested that such missions need not be subject to the same stringent requirements as government missions, calling for “reasonable protocols and processes” for commercial missions.
“What we do, and what ESA is doing, in some cases are requirements that would be virtually impossible for a commercial mission to meet,” she said. “We have to figure out how to work closely, how to move forward in a collaborative posture so we don’t have another red Roadster up there in orbit.”
That is astonishing as the planetary protection office has as part of their own guidelines that you need a protection plan, even for a category II mission to the Moon. You don't currently need to take any precautions to prevent contamination of the Moon by your spacecraft or contents, but still, you are required to file a plan that says where it is going to land, where it travels, and document any crash, for information purposes. That's for later missions. For instance, if they find organics in such and such a crater they can look up the planetary protection plans and say "Ah that's from that SpaceX rocket, it landed in the crater over there ".
Let's quote from the Planetary Protection Office guidelines on the requirements for a category II mission e.g. to the Moon:
"Category II includes all types of missions to those target bodies where there is significant interest relative to the process of chemical evolution and the origin of life, but where there is only a remote chance that contamination carried by a spacecraft could jeopardize future exploration. The requirements are only for simple documentation. This documentation includes a short planetary protection plan is required for these missions, primarily to outline intended or potential impact targets; brief pre-launch and post-launch analyses detailing impact strategies; and a post-encounter and end-of-mission report providing the location of inadvertent impact, if such an event occurs."
The problem is that this is the first time a private space company has done anything that really needed a planetary protection plan. So it's an unprecedented situation.
She wants to get the private space companies more actively involved in planetary protection. But she doesn't want to be a sheriff bearing hard down on the private space industry. She wants to work with them, much as the planetary protection officer works with NASA.
This is what gave people the idea that she would be open to relaxing the planetary protection provisions, especially with her remarks about the difficulty of applying the current requirements to private missions. But the example she gave didn't suggest that at all.
The only concrete example she gave was the Tesla Roadster and she said she “We have to figure out how to work closely, how to move forward in a collaborative posture so we don’t have another red Roadster up there in orbit.”
Now, as it happens, it was followed for a long time by astronomers and they could determine a precise orbit. Based on that, the chance of it impacting Mars in that orbit, even in the next ten million years is negligible. Hanno Rein et al have done the analysis and got a chance of hitting Earth in the next 3 million years of 11% and of hitting Mars minute. Longer term it's got a high chance of hitting the Sun. Even longer term, if it survives that long, it could venture into the outer solar system or be ejected from our solar system altogether. Ten million years is plenty of time to thoroughly sterilize it through ionizing radiation, as I don't think the shell or even the engine of the car would provide much by way of protection over those time periods, especially against cosmic radiation.
- Musk's car to drift for millions of years
- Paper here
- Elon Musk's Cherry Red Tesla Roadster Could Be Interstellar Traveler A Billion Years From Now - If It Doesn't Hit Sun Or Planet (my article on it)
Here is a video about the Roadster that Elon Musk just made.
Incidentally if you wonder how the spacesuit can look so much like normal clothes - the spacesuit worn by the manikin is an IVA spacesuit, not meant for EVAs, only usable with an umbilical and meant for surviving sudden decompression when inside a spaceship, e.g. during launch, docking maneuvers and re-entry. .
There's been some criticism of his launch of the car in orbit, but I don't see any problem with it myself, more imaginative than a lump of concrete and some barrels of water, which is what most space companies would have sent on a first launch of a rocket.
So long as it is okay as regards planetary protection, that's the main thing.
As far as planetary protection is concerned, it is not that different from the final stages of most spaceships sent to Mars. Nearly all, with the notable exception of MOM, the Indian spaceship, travel on much the same trajectory as the spaceship itself. They are trajectory biased to miss Mars for planetary protection reasons and are not sterilized. As with the Tesla Roadster, they may hit Mars eventually but the chance in the near term is low.
The current rules for orbiters and flyby missions to Mars are that there has to be a chance of less than 1% of hitting Mars within 20 years and less than 5% of hitting it in 50 years. Now - whether those rules need to be changed is another thing, but that's not the job of the office. It is to help with making sure missions comply by the rules as they are right now, whatever they are, and the Tesla Roadster would have passed the current rules with flying colours. Not just with the orbit it ended up on. Just as happens for the final stages, I think a detailed analysis would probably have determined that any orbit it ended up on would be fine for at least 50 years. That's because although its trajectory wasn't controlled at all and it just burnt its fuel until it was all gone, it was launched at a time when it was just about impossible to get to Mars, except perhaps on a ballistic capture trajectory, but those are very hard to get into needing precise synchronization. In any case, it would just need to be launched into an orbit with a different inclination from the Mars orbit to have almost no chance of hitting Mars any time soon.
But it should have a planetary protection plan all the same, so that everyone knows that they have considered this matter and knows how it is that they plan to avoid contaminating Mars with Earth microbes from the Roadster. We want to know that it wasn't just an accident that it ended up in an orbit that is safe for Mars. It is nothing to do with it being a Roadster. If he'd sent some lumps of concrete and barrels of water, still it would have needed a planetary protection plan if on an orbit that had a chance of hitting Mars.
So, I think her concern is not so much the Roadster, in the orbit it ended up in, but the precedent. Similarly if ROSCOSMOS (Russia) or ISRO (India) or JAXA (Japan) or ESA (Europe) or CNSA (China) were to launch cars into an orbit as far as Mars or beyond, or indeed, lumps of concrete or barrels of water, we'd all want to have enough of a planetary protection plan from them to understand what provisions they have taken to make sure they won't contaminate Mars. Or if it crashes, say on the Moon, we all need to know where the crash site is so that we can work around that and allow for it in investigations of that area of the Moon.
This just makes sense. It is astonishing to me that this wasn't done, that they weren't working closely with the planetary protection office to just run their plans past them and get their feedback and "okay", and indeed to have it on record for future scientists to refer to.
SO WHAT DOES LISA PRATT MEAN ABOUT NOT BEING A SHERIFF?
So what did she mean? She couldn't have been suggesting that the US ignores its obligations under the Outer Space Treaty or ignores the results of the deliberations of COSPAR. That is not her remit and indeed, it is not something that is within her power to decide. She can't change the US commitments under international law.
To do that would be like a quarantine officer deciding on the spot to change the quarantine laws to let someone's pet through because they took a liking to its owner or thought it was cute.
"Oh this cute puppy. The rule is that you can't bring a puppy into the US if it is younger than four months because you need to vaccinate it against rabies first and the first injection can't be given until it is three months old. But I'll make a special exception because I like it and like you - you don't seem like the type of person to have a puppy with rabies and I'm sure this cute puppy can't have rabies anyway, look, it's so adorable - just go ahead and take it in this one time".
What would you think of a quarantine officer who behaved like this?
A planetary protection officer can't do that either. It doesn't matter how much she likes you.
Now, if you look at it more carefully, it's not quite like quarantine. The quarantine laws are clearly spelt out for everyone. But with the Outer Space Treaty, the details of how it is to be implemented in the US are not so clearly stated. It is for NASA. For planetary protection, then NASA has developed its own NASA Policy Directive (NPD) 8020.7G: Biological Contamination Control for Outbound and Inbound Planetary Spacecraft. As the Planetary Protection Office put it:
The NASA policy, and its associated guidelines and requirements, are well aligned with the COSPAR Planetary Protection Policy, and is consistent with Article IX of the ‘Outer Space Treaty’.
That is clear enough. But the NASA policy directive only applies to NASA. This treaty and Article IX are an obligation on the US as a whole, not NASA particularly, but what is the situation for private space companies? Are they also well aligned with the COSPAR Planetary Protection Policy?
So, I wonder if she is suggesting that we need something similar to the NASA policy directive for the private space industry? Not to ignore COSPAR, but to look in detail at how it is applied to private space, what the processes are and the obligations etc?
At any rate, I think that above all, what Lisa Pratt means by her Sheriff remark is that however it is done, she wants to bring private industry on board with the process, so that they are involved, along with everyone else.
If we are all in this together, SpaceX would want to file planetary protection plans because they also would care about protecting Mars. They would care because they have had many conversations with the planetary protection department during which each comes to understand the other's perspectives, and they would recognize planetary protection as something that affects us all, and our children and grandchildren too. She would also presumably take their concerns and proposals to the COSPAR meetings so that the international deliberations of the astrobiologists are based on what matters to the private space industry, trying to answer the questions that are important to them.
So, I'm glad to hear she will be working towards closer integration with the private space industry. And as an astrobiologist I think one can be sure that her top priority will be to preserve the astrobiological interest of Mars, and to make sure we do not mess up our search for life there.
As we will see, Elon Musk also thinks we should not extinguish Mars life. He thinks that we should do what we can to prevent that. As you'd expect from someone with an interest in space and science generally. So he should be on board with this approach, you'd think.
TECHY ASIDE ON SPACE LAW AND THE "HARMFUL CONTAMINATION" CLAUSE
Perhaps we even need new legislation to clarify obligations for the private space sector for interplanetary contamination. One space lawyer Laura Montgomery has a controversial reading according to which it is not clear whether or not the clause on "harmful contamination" which is the basis for all the planetary protection guidelines and the COSPAR deliberations applies to individuals, though she agrees that another clause on "harmful interference" is most naturally read as applying to individuals as well as States. The
It may seem just a niggle, but the thing is that in the Outer Space Treaty text, it says that States are obligated to prevent harmful contamination, but in the case of harmful interference the statement only triggers an obligation to consult before they act, i.e. to talk about it first.
It suggests a scenario where the US tells everyone else that a private company is about to launch a mission to Mars that will introduce trillions of microbial spores and interfere in a harmful way with their science experiments - but then does no more than just keep them informed of what is going on. According to her interpretation, there may be no other obligation on the US government, so long as it is a private rather than a government organized mission.
If Laura Montgomery is right, then the only way to clarify the situation in the US would be for Congress to pass a law spelling out what the obligations are on this matter for private individuals in space.
Other US space lawyers say that both clauses apply to individuals as well as to States, so that the US already has an obligation to ensure that individuals as well as the government organizations act to prevent harmful contamination.
For more on this see my Does planetary protection law for individuals need to be clarified in the US? where I summarize what she said in discussion with me, and provide links to her blog post, and SpaceShow talk. I also quote from an interview in which she and another space lawyer give opposite views on this question. (which shows it is a controversial interpretation).
I'm no lawyer. So can only comment as an ordinary person :). Anyway just to say I'd have thought it unlikely that Laura Montgomery's interpretation iis what the drafters of the treaty had in mind. It would be like a quarantine rule where you say that government entiteis can't import Hawaiian fruit to California for their banquets, as a measure to stop the invasion of the Oriental Fruit Fly - but anyone else can import as much fruit as they want.
What would be the sense in that?
FAQS FROM KEEN SPACE COLONISTS
I'd better address some points right away as they are the top FAQ's when you talk about the need to protect Mars from Earth life.
If I don't address this now, along with some follow up points, I think many of my readers will stop reading, the ones who are keen space colonists, who are amongst the ones I think it's most important to be involved in the discussions..
If you want to continue with the planetary protection discussion, then skip this section and the next few, and go on to the section: "LISA PRATT ON OPEN QUESTIONS FOR PLANETARY PROTECTION " below.
MARS CAN'T BE TERRAFORMED ANY TIME SOON
Many of you may think we have to send humans to Mars urgently as a way to become interplanetary, to avoid disasters on Earth. You may think that this is so important it overrides all other considerations. That has to be the number one reason people give for dropping planetary protection in internet conversations on the topic.
You may have been persuaded by Elon Musk, who says his main reason for developing SpaceX is to find a way to become a multi-planetary species. Also, perhaps, by science fiction stories, which influenced him too. You may well think of the series of three books, Red, Green and Blue Mars by Kim Stanley Robinson that came out in the mid 1990s. In this he envisions Mars terraformed and developing a planet spanning civilization. The main focus is on social issues but he has a backdrop of terraforming with plausible sounding science, and this has influenced many people to think that terraforming Mars would be easy and accomplished on a short timescale, in as soon as a couple of centuries. See Mars trilogy - Wikipedia
The Martians cover - this is a sequence of short stories set within the fictional world of the Mars Trilogy.
Kim Stanley Robinson himself says that it would take far longer than his trilogy suggests, which is based on 1980s ideas. He says that we can’t use Mars as a ‘backup planet’. We have to fix our problems on Earth to have any hope of surviving on the timescales of the book. See the podcast here and summary on Io9 here
When you start to look into it carefully, you find that it's a huge megaproject, billions of dollars a year, for thousands of years. I mean, the scale of what they propose is utterly staggering. When we have trouble keeping to a single direction for space projects in the US for two presidencies, they are proposing setting out a project that needs a unified direction in space for thousands of years to get completed.
They propose construction of planet sized mirrors orbiting Mars, or hundreds of factories mining cubic kilometers of fluorite ore and using hundreds of gigawatts of power continuously for at least a century to make greenhouse gases. Then, if you are optimistic you end up with a planet where trees can grow in the equatorial regions but no oxygen, no way to breathe without a full closed cycle rebreather with nitrogen inside (CO2 is toxic above 10%), and to get this far takes a thousand years and probably getting dozens of comets and impacting them into Mars for their volatiles.
It is a fun thing to do on paper. But in real life? I am not sure such a project would even last as long as 8 years.
And - all that effort to create two or three meters thickness of atmosphere (you don't care about the rest), filling the dry sands to depths of hundreds of meters with water in order to get lakes and eventually seas on the surface. Sourcing teratons of nitrogen somehow in order to get a buffer gas in the atmosphere as a fire retardant to prevent the fires you get easily in pure oxygen. And it assumes we can somehow set up a biosphere and direct it for thousands of years, and avoid any problematical microbe taking it over, and, say, making hydrogen sulfide, or methane, or eating our microbes,or eating up any oxygen as fast as we make it, or indeed, mutating to be pathogens to humans or mold that infests our plants or some disease of the green algae that make them less efficient at photosynthesis etc. For thousands of years none of that has to happen, or we find a way to contorl it.
Once you have trees and plants, you can't breathe yet. You need to sequester many meters thickness of organics out of the air just so humans can breathe. And source nitrogen from somewhere because CO2 is harmful to us above 10% (and that's not a mistake, I do mean CO2 not CO - it's only a trace gas in our atmosphere and we can't bear it in high concentrations).
And for what? If you can ever achieve your "terraformed Mars, perhaps a hundred thousand years into the future, you aren't done. You can't stop the megatechnology. You still have to continue to make those greenhouse gases or maintain those planet sized mirrors into the indefnite future, as Earth's atmosphere is nowhere near warm enough on Mars. Without the greenhouse gases or the planet sized mirrors, it would be too cold for trees even at the equator.
Now, don't get me wrong. On an intellectual level the ideas are great fun to read. And you can imagine what it migth be for someone in a long lived civilization that has been around for millennia to start on a terraforming project (which would still be a huge speed up on the millions of years that it takes naturally). But I think for us right now it is far more fantasy than reality. For more on this:
Who knows, perhaps some day we can terraform planets, but I can't see it any time soon. But what we can do right away is to make city domes, lava tube dwellings, and free space habitats. Those are far easier to do and can be made anywhere in the solar system. They can be completed in a decade, and for far far less cost than any attempt at a terraforming project.
We don't know if Mars gravity is suitable for human health. But a spinning habitat, either a torus, cylinder, or just two habitats tethered together, can be set up with any level of gravity you like. You can also use centrifuges to augment gravity on the Moon for sleeping, eating, exercise, or using the toilet. There are many such ideas to explore.
Surely those simpler approaches are where we start, rather than a grand thousands of years project to terraform a planet? And if you start there, there's no urgency to do it on Mars. We can start anywhere, and the Moon is one of the best places to start.
HARSH CONDITIONS ON PRESENT DAY MARS - FAR BEYOND ANYTHING YOU ENCOUNTER IN AN EARTH DESERT, EVEN ANTARCTICA OR THE TOP OF MOUNT EVEREST
Mars is just extraordinarily harsh. Human lungs can't function there and there is no way to adapt. The air is so thin that the moisture lining your lungs boils at blood pressure. Even with an aqualung or a complete closed system rebreather, you can't take a single breath of oxygen nor can you exhale a single breath of carbon dioxide.
You can't even use the air already in your lungs, indeed it can be dangerous to hold your breath - your best advice would be to exhale immediately as the air in your lungs is useless and potentially dangerous if it damages your lungs as it expands. You lose consciousness within 15 seconds, as soon as the oxygen in your blood is used up, the circulation of your blood stops within a minute, clogged by bubbles in the veins, and you are dead in minutes.
You need a full pressure EVA suit - and not the IVA suit shown by SpaceX which is only good for surviving a depressurization incident in a capsule. These are eye-wateringly expensive at about two million dollars each. Basically they are mini spaceships. They have to supply oxygen, protect from micrometeorites, scrub CO2, cool down the astronaut and at the same time let them flex their joints with an outwards pressure of over a ton per square meter (it's far easier to just create an enclosing balloon with the astronaut inside it). See What is a Spacesuit? (NASA).
If that is reduced say, to $200,000 each with mass production of spacesuits, that's about the cost for an average house in the US. Currently they are good for a couple of dozen EVAs in zero g outside the ISS, doing light work. Maybe they will be good for a few months use with improvements of technology but still need lots of maintenance especially with perchlorates laced dust getting everywhere. And it's not likely you can just put it on like a coat in the near future, as they do in sci. fi. In the ISS they start preparing for their EVA the previous day, with many safety checks, and the astronauts camp out in the airlock before the EVA to give their bodies time to adjust to the lower pressure levels used in the spacesuits for mobility.
Then it gets so cold at night that the carbon dioxide forms dry ice frosts on the landscape for many nights of the year and the dust storms occasionally block out the sun for weeks on end. The landscape looks like a desert in the US but it is far more like the Moon as a place to live.
Indeed, in many ways, if you do a detailed comparison, the Moon actually turns out to be significantly more habitable than Mars as a place for a first off World settlement, I was surprised to find out, when I wrote Case For Moon First.
So there is no human urgency to get to Mars to survive. The Earth is where we make our stand. We can explore space but only with a secure planet that we protect as our base in our solar system. Earth is the backup for any prospective Mars colonists and it won't be the other way around any time soon.
I should perhaps briefly touch on Zubrin's arguments too. He presents them in numerous talks and debates as if they were "knock down arguments". But they are far from it. They are as full of holes as a collander.
ROBERT ZUBRIN'S INFLUENCE ON THESE DEBATES
Robert Zubrin (head of the Mars Society and author of "Case for Mars") in particular has argued strongly that in his view there is no risk of contaminating Mars with Earth life. Although he is an engineer and a space colonization advocate, he has had a lot of influence on the debate about appropriate protection of Mars.
I think it is important to realize that his is just one person's perspective, based on his optimistic view that
- Earth life has already been transferred to Mars on meteorites
- It is identical to its cousins on Earth
- We would be able to distinguish any native Mars life from Earth life by gene sequencing it
- Earth life can't make Mars life extinct because it is adapted to Mars
He gives plausibility arguments using vivid analogies that convince prospective colonists that are keen to get to Mars as quickly as possible. He presents them with great conviction and panache as if they are knock-down arguments that nobody could ignore. But actually, there are many flaws and weaknesses in them if they are considered carefully.
In particular he uses transfer of meteorites to argue that the habitats on Mars already have Earth life and that therefore nothing we can send there can harm them. This is not only not established; it would be a major discovery and surprising to many, if we found that Earth life has got to Mars on meteorites. It is rather easier in the other direction. It's not easy for life to survive on a rock that punches through the atmosphere so fast it exits the atmosphere at 11.2 km / sec. and so is a blazing fireball throughout. And if any life did get there, it certainly doesn't mean that all species of Earth microbes able to survive on Mars get there. For instance, it's unlikely that photosynthetic life would survive the transition from Earth to Mars because it tends to live on the surface of rocks and would be ablated away by those blazing fireballs as they exit the atmosphere.
I will go into gene sequencing and the meteorite transfers later in this article - and I cover his arguments in detail in these sections of my book:
- What are Zubrin's arguments?
- Demolishing Zubrin's arguments
- What about Zubrin's meteorites argument?
- :Zubrin's arguments in: "Contamination from Mars: No Threat"
- Some highlights from the rebuttals of Zubrin by astrobiologists in "No Threat? No Way"
Those take you to my online book in my Touch Mars? Europa? Enceladus? Or a tale of Missteps? (warning, it's around 2000 pages as a single web page, give it time to load).
LISA PRATT ON OPEN QUESTIONS FOR PLANETARY PROTECTION
Her interview about her new job, posted on the Indiana University press release doesn't give answers. She talks about the question "Do we know enough about the possibility of present day life on Mars to safely take astronauts there?".
"It seems to me that the most important question we as humans could ever answer is, "Are we alone?" Do we know enough about the possibility of present day life on Mars to safely take astronauts there?
I have a burden, a burden of responsibility, to figure out how we collaborate with all the other nations and individuals who are capable of reaching Mars, to ensure that we understand what's there before we bring bits and pieces or intact spores of Earth organisms to Mars, and inadvertently inoculate a habitable planet.
During my time at IU (Indiana University) there are two things that I am most proud of. One is the recognition that there was a complex eco-system in these very, very deep, hot fluids in South Africa. But that then lead to the realization that Earth is unusually hot in the subsurface. And if we are interested in Mars. then Mars is a much colder planet. We then proposed similar work in deep mines in the Canadian Arctic. That was a real turning point for me, because that research was closely coupled to things that NASA wanted to know. That was the critical point when my career shifted to the exploration for life in places on Earth where people really hadn't done much looking.
The other thing I am most proud of is in the field campaign in Greenland right on the margin of the Greenland ice sheet.
I am so excited about the opportunity to be in the room when the decision-making conversations are taking place. To be actively participating in thinking about what are our rights and responsibilities at the moment in time when humans become space faring.
She raises the question of whether we know enough to safely take astronauts there. She didn't answer it, and all the COSPAR discussions so far on humans to Mars have concluded that we still have many knowledge gaps. So, at this stage anyway, she couldn't answer it.
IS THERE REALLY ONLY A BRIEF WINDOW OF TIME WHEN WE CAN STUDY EXTRA TERRESTRIAL LIFE ON MARS IN ISOLATION FROM TERRESTRIAL LIFE?
This comes from other quotes from her on the Indiana University press release about her appointment:
"The importance of planning for the protection of Earth's biosphere, and for responsible exploration of Mars and other locations in our solar system, cannot be overemphasized,"
"With only a few decades left until there are boot prints on Mars, it is imperative for the international scientific community to plan for the unknown consequences of contact between two life forms and their biospheres. It's possible that 'first contact' has already occurred due to the unavoidable presence of spores and cell fragments on spacecraft launched from Earth and landed or crashed on Mars.
"If life does exist on Mars, which is a big 'if,' then we have a brief window of time remaining in which extraterrestrial life can be studied in near-isolation from terrestrial life,"
For me that is so sad, to hear her say that.
It is not a great surprise actually, as it's in other NASA announcements by the planetary protection officers in the past. It seems to be how they are thinking about the plans of either the government or the private space industry or both - that one way or another we will send humans to Mars in the near future. It's like a given, a fixed point in future history that they feel they have to work around.
Knowing what they now know about Mars, that Earth extremophiles can survive there, definitely as spores for thousands of years, and possibly also revive and colonize habitats there, spread in the occasional global dust storms - they conclude that it is inevitable that eventually we will irreversibly introduce Earth microbes to the planet. From that, it follows that we have only a brief moment of time to study Mars in its current uncontaminated state before humans get there.
Why this urgency? Why "only a brief window of time"? This is the question nobody seems to ask in this debate.
THIS IS OUR DECISION AS THE HUMAN RACE - ANY BIOSPHERE COLLISON IS OUR OWN RESPONSIBILITY AND NOBODY ELSE'S
If we lose the opportunity to learn about Mars life, it is of our own doing. Nobody else and nothing else is imposing this on us. There are so many other places we can send humans in the solar system. Starting with the Moon, the moons of Mars, Venus clouds, Mercury, Jupiter's Callisto and beyond, including free space habitats too.
What is the urgency to land human boots on Mars as fast as possible? Can't we do both, send humans into space, learn about sustainable living on the Moon - and eventually send humans further afield. But on Mars, to study it from orbit, by telepresence, so that the astronauts there are part of the adventure of searching for life too.
12th April 2011: International Space Station astronaut Cady Coleman takes pictures of the Earth from inside the cupola viewing window.- I've "photoshopped" in Hubble's photograph of Mars from 2003 to give an impression of the view of an astronaut exploring Mars from orbit.
They can speed up the robotic searches hugely by guiding them from orbit, secure in the knowledge that what they are doing does not in any way risk endangering the search for life there. And meanwhile we are finding out about Mars and placing various assets on the surface, all of which would be useful in the future if we do send humans right down to the surface.
Also, if there is life there, we learn about its capabilities and its vulnerabilities before embarking on this hard to predict collision between the Earth and Mars biospheres. If there isn't life, we learn about the conditions on Mars and can begin to try to work out how Earth microbes would interact with them and what they would do to Mars (if anything).
If we do it this way, learn about Mars first, we can have a far better idea of what is there and maybe avoid future issues such as accidentally turning the water supplies on Mars to cement (more on this later). And if we find some vulnerable but incredibly interesting life there, then I think almost everyone will be on board with the need to protect it and study it carefully. And then we can develop proper planetary protection plans for this life, based on knowing what is there and what its capabilities and vulnerabilities are.
Is this "boots on Mars" and rapid colonization attempt what our children and grand children would want - if this is indeed the implication that we would lose the opportunity to find some wonderful discovery on Mars? Is it even what Elon Musk himself would want if that's the end result?
I write this article as a way to help get more public awareness of the perspective of astrobiologists and the planetary protection officers. Also to get us all thinking about it and talking about it.
The geologists and the colonization enthusiasts have their unique perspectives too, but there is so much more to space exploration than geology and colonization attempts. We need to get a complete picture on this if we are to avoid making maybe tragic mistakes as we explore the solar system. I think the more of us get involved in this debate, with all our various perspectives that we bring to it, the more likely that we can end up making wise decisions in the future.
WE SIMPLY DON'T KNOW ENOUGH
So - now we get to the nitty gritty of the central problem that has dogged several COSPAR workshops on what provisions are needed for human missions to Mars. It's the issue the planetary protection officers constantly grapple with. We simply don't know enough.
Their reports come out with long lists of knowledge gaps. And actually, I don't see myself how they can be filled in a short timescale such as the next decade, say. Mars is such a large planet and the few missions so far have only just scratched the surface, and we have not yet sent a single modern astrobiology instrument to Mars or sent anything to search for life in the places we think present day life just may be possible. Indeed we haven't even looked for it properly where our current rovers are.
Curiosity could be driving over sand with dormant spores in it every day, and we simply wouldn't have a clue yet. Because it is not equipped with any instrument that could detect life. We do have several that could be sent, and a couple (UREY and the Life Marker Chip) got close, UREY very close to getting onto a mission to Mars, until NASA pulled out of the joint mission with ESA - but astrobiologists have never yet managed to get any of their many instruments onto a mission to Mars. Not since the two Viking landers in the 1970s.
For more on this see
EXAMPLE OF EARLY PRE-DNA LIFE ON MARS - ALREADY EXTINGUISHED ON EARTH
One example which for me shows strikingly that we just don't know what our microbes could do to Mars is the possibility of some early form of life there that's not yet evolved as far as DNA. We must have had such life on Earth, indeed quite possibly many different such life forms, independently evolved, but if so, it is now all gone (the idea of a shadow biosphere popular a decade ago doesn't seem to have panned out). But it could still be there on Mars. Either as a shadow biosphere of some early form of life that still survives there, though not on Earth, or it could be that this early life is the only form of life there.
In either case it is potentially vulnerable to whatever made early life like that extinct on Earth. Because Earth must have had a simpler biology than our modern DNA based life. Everyone agrees on that, because modern life with its numerous intricate interconnections is just far too complex to arise in one go. These early life forms are no longer here only because modern Earth life made them extinct. Again there is no other possible explanation, since modern Earth life survived and early life didn't. Since modern life evolved from it, at some point there must have been both types present here, and then the earlier life was made extinct by modern life.
This proves that it is possible for modern microbial life from Earth to make some other forms of life extinct. And not just a few species. It can make the entire biosphere extinct so that there is not a trace of it left, only Earth life. Because that has already happened here on Earth. The one thing we don't know is how long it takes.
WHY MARS LIFE COULD BE EARLY LIFE
You may remember Bill Clinton's announcement of a discovery of life in the Martian meteorite ALH84001 - which was later retracted as not yet proven. Well even though we still don't know if it is life or not, it lead to a lot of interesting discussion and a workshop to try to figure out if such structures could be life.
Here are is one of their images from the original press release:
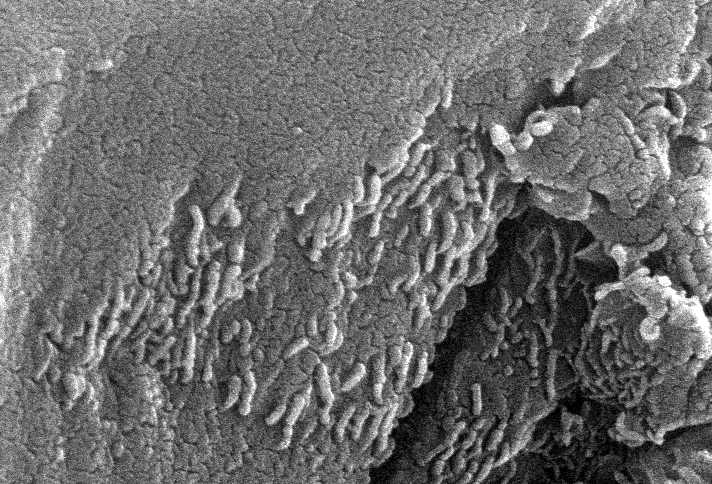
The structures in these photos are between 20 and 100 nm across, well below the resolution of a diffraction limited optical microscope of 200 nm.
These were tiny cell-like structures that some thought might be an early form of life because they were too small to contain all the biological "machinery" needed for modern DNA based life to reproduce. Although there is now an alternative geochemical explanation, it's an alternative, it's not a disproof that those structures are remains or fossils of life. Future discoveries on Mars could end up giving us the extra evidence needed to prove that they are life, if indeed they are.
The workshop convened on limits of size for cells showed in great detail that such small cells could indeed be life. Early pre-DNA life could be as small as tens of nm in diameter, like these cells.
So, they still could be life. They just weren't able to decide conclusively either way and the question remains open with opinions on both sides of the debate.
Now, of course they might not be life. The geophysical hypothesis may be correct. But whether they are or not, it does show the possibility that in the future we could find such structures in Mars meteorites, or on Mars itself, and this time be able to prove that they are indeed life.
This is normally given as a suggestion for past life on Mars, 4 billion years ago, the date for the Mars meteorite ALH84001. However, if we can find fossils like that, and if Mars is still habitable as some think, then it's at least a possibility that we can find present day life that is still like that on Mars.
That is, unless modern Earth life got to Mars long ago, and already made it extinct long before we came on the scene. Is this possible?
POSSIBILITY THAT NO MODERN EARTH LIFE GOT TO MARS
It's a major challenge for microbes to travel in the direction from Earth to Mars because of Earth's gravity and atmosphere. The rocks have to leave the atmosphere at the escape velocity of 11.2 km / sec. That's only possible for the debris of a large impactor, probably the likes of the Chicxulub impactor that hit Earth at the end of the dinosaur era, 66 million years ago. Also the rock has to leave Earth's surface at an even higher velocity, so has to be a blazing fireball all the way through the atmosphere. The shock levels as the rock is suddenly ejected from Earth by the impact are likely to be huge also.
Any life that did survive all this would have to be well within the rock where it was not burnt off by the fireball ablating its outer layers. In particular photosynthetic life is very unlikely to make it to Mars as it tends to live on the surface of rocks, or in cracks that would be reached by plasma from the fireball. And life that does get there is likely to just stay trapped inside its rock, landing on a dry cold dusty Mars with almost no atmosphere - unless this happened billions of years ago when Mars was more habitable. After surviving all that, then it also has to be sufficiently pre-adapted to the conditions there to thrive.
It's not impossible for a hardy microbe but it's no sure thing either.
OR EARTH LIFE GOT THERE BUT MARS LIFE SURVIVES AS A SHADOW BIOSPHERE
It's also possible that there was some exchange of life, especially after the huge impacts over three billion years ago - and that whatever life got there plays nicely with whatever is on Mars, leaving the earlier life, whatever it is, as a shadow biosphere.
When astrobiologists design instruments to search for life on Mars they design them to be as general as possible. They reason that if they design them to look only for Earth life, they may miss out on the most exciting discovery possible, of life that is not like our form of life in some interesting way.
So, at least on the basis of what we know so far, there could be early life on Mars, either co-existing with DNA life as a shadow biosphere, or it may even have never encountered DNA.
Either way it would be vulnerable to whatever made it extinct here. So, based on what we know so far, it has to be possible that introduced Earth microbes make Mars life extinct.
EARTH EXPERIENCE NOT ENOUGH TO PREDICT EFFECTS OF A COLLISION OF BIOSPHERES
Our experience studying microbes on Earth is not sufficient to test these ideas thoroughly. We do get invasive diatoms here as well, and they can prove a nuisance, for instance a diatom that is taking over fresh water lakes in New Zealand seems to have been introduced recently in the last decade or so on wet diving gear from the northern hemisphere. For more on this, with cites, see Invasive diatoms in Earth inland seas, lakes and rivers in my Touch Mars? book.
But this would be something over and above anything that is even possible on Earth. We simply don't have any examples of any life on Earth that would be as vulnerable to our microbes as some of the possibilities for what we could find on Mars. Nor can we make such forms of life in the laboratory.
The only life we can make is based on DNA, or small modifications such as adding two extra bases to the DNA base code (one of the most major accomplishments in recent years in this topic area - They added various features to their microbe including a "spell check" that let it hold onto the new bases for 60 generations which they think means it can hold onto them indefinitely).
There are plans eventually to replace DNA itself by the same code but using a different backbone, PNA perhaps. If so it would still be basically DNA based life doing all the same things, same cell processes, the same amino acids, RNA sequences and "language", but with PNA making up the genes instead of DNA. It would be nothing like as radical as a separately evolved or precursor lifeform. What we find on Mars could be wildly different, not even using the same basic building blocks. see Alien life could use an endless array of building blocks. We can imagine various possibilities, but as to actually building a test "RNA world cell", say, to see if it works, it is way beyond us.
It's not like putting lego pieces together to make a model - because the components are active, chemicals, doing things, reacting together, as soon as you put even two of them into the same place. It's more like trying to "herd cats" than to build something out of lego or Meccano.
EPS award winning "Cat Herders" commercial . Making a living cell from its chemical components, even if you know how it works, would be like herding cats. And we don't even know how an RNA world cell would work in detail.
Once we have a living cell we can make more just by letting it replicate, and we can modify it. But to make even the simplest cell from chemicals - no - that's way beyond us.
So, we can't use Earth bound analogies as a way to prove that it is safe to introduce Earth microbes to Mars. Because we have no proper Mars surrogate on Earth to test the ideas on.
COULD ANY MARS LIFE MAKE DNA BASED LIFE EXTINCT?
This section is inevitably speculative. But we can't avoid that in this topic area. We may be about to go into a future that so far has only been the subject of science fiction stories.
So, there is another implication here too. If it's agreed that Earth microbes can make earlier forms of Earth life extinct, and so, potentially, Mars life too - what is to stop some even more advanced form of life making Earth life extinct? Not a super intelligence, I just mean a more evolved type of biology in every cell.
Although you can make a good case for Mars life being less evolved than Earth life, you can also make a case in the other direction too. Mars has had many periods of variation in habitability. Some think that the "slush ball" or "snowball" Earth was what lead to the diversification of multi-cellular life in the Cambrian explosion. Well in that case Mars has had numerous potential "Cambrian explosions" in its brief periods of habitability. According to some ideas, for instance, early Mars was totally frozen over for hundreds of thousands of years. It's orbit varies in eccentricity over long periods of time, sometimes almost circular and sometimes very eccentric, leading to one or other of its hemispheres having exceptionally warm "summers. According to one of many theories about how early Mars was warm enough for liquid water oceans - at times when its orbit was particularly eccentric it becomes habitable every two years when closest to the sun. Other ideas include greenhouse gases, and they also may have had "snowball Mars" phases.
If it did happen this way, might all those "snowball Mars" phases have accelerated evolution?
Also might there be variations anyway in the rate of evolution? Could Mars life have some feature that is as advanced over Earth life as the cell nucleus of eukaryotes is over prokaryotes? Or might it just have life with vastly more non redundant genes in their DNA (i.e. ignoring "junk DNA" and duplicated genes)? There has been a steady increase in the complexity of the genome of Earth creatures over billions of years, as measured in this way, and there is no particular reason to suppose this has stopped.
So what happens when Earth life encounters another form of life with vastly more complex genomes than anything that has yet evolved on Earth? Equivalent to whatever will evolve on Earth a billion years from now perhaps?
Or could it be a mix, Mars life is more capable in some respects, and Earth life is more capable in other respects?
For a concrete example, suppose Mars has a new form of life more capable at photosynthesis than any Earth algae in the sea or our land plants either? This is not implausible because with the low light conditions, frequent dust storms blotting out the sun, and the thin atmosphere, this might put efficient photosynthesis at a premium. For instance, our purple haloarchaea use mainly green light, and our plants and other algae use mainly the remaining red and blue light (reflecting away green light, the brightest part of the solar spectrum). Our seaweeds, in low light conditions, are often dark brown and some plants are black, using helper "antenna" pigments to get as much photosynthetic energy as possible.
Perhaps Mars life is also black and uses the full spectrum of all the light that falls on it?
We know that our plants have reached nowhere near the theoretical limit of efficiency for photosynthesis. Artificial enzyme paths have been designed using chemicals from many different lifeforms on Earth, mixed together in ways that they never could in nature, to make a form of photosynthesis that is 20% more efficient than Earth plants
"The end result was a synthetic CO2-fixing cycle, something which, as far as Erb is aware, "nobody has ever achieved before." A total of 17 different enzymes, including three "designer enzymes", are used from nine distinct organisms including human beings. The bottom line is that the CETCH cycle, where the Marburg-based researchers emulate photosynthesis's dark reaction, fixes CO2 at 20% greater efficiency than the Calvin cycle in plants."
That could be enough of an advantage to edge out Earth life. But if it uses some radically different principles, it might be far more effective than that. Earth photosynthetic life is only one percent efficient at converting sunlight to biomass. The Bionic leaf version 2.0 is able to convert 10% of the sunlight to biomass, using a catalyst made of cobalt and phosphorus with the help of a bacteria Ralstonia eutropha.
Also there is no reason for photosynthetic life to produce oxygen. Some consume hydrogen sulfide converting it to sulfur (CO2 + 2H2S = CH2O + H2O + 2S, the traditional photosynthetic equation with the O that enters into the reaction replaced by S).
More radically,the salt loving haloarchaea convert light directly into energy (through a proton gradient) much as the cells in our retina do, not producing any chemical byproducts at all. So, what if some Mars microbe is more efficient at converting light into biomass than our plants or algae but does not produce oxygen, and is inedible or poisonous to Earth life? It doesn't have to infect humans to be harmful.
It is also possible that unrelated Mars life is a pathogen of humans. It doesn't have to be adapted to us to do that. Take the example of Legionnaires disease, a disease of microbes and biofilms that uses essentially the same methods to live in human lungs. This shows that it is also possible that microbes evolved to infect biofilms on Mars could live in and on humans too, and if so, it's not impossible that it is harmful to us, accidentally. Often microbes evolve to become less harmful to their hosts rather than more so, as it is not in their interests to kill their hosts, and eventually, they may co-exist as symbionts.`
There are many other ways in which Mars life could be harmful to our astronauts or to Earth. For instance by producing toxins. Chrys Chyba gives the example of green algae in the Great Lakes in the US that produce toxins that kill dairy cows. They are of course not natural predators on cows; it's just an accidental poisoning. Well the same could happen with Mars microbes and humans.
The life need not use the same biochemistry to be hazardous in this way. It might indeed be a more likely issue for unrelated independently evolved life, which might produce chemicals that closely resemble amino acids, say, and confuse our biology.
How could that happen? Well, if you eat a lot of sea food from fish that have fed on algae blooms, in rare circumstances, it can lead to a neuro-degenerative illness, especially Lou Gehrig's disease which causes progressive muscle weakness. The culprit seems to be BMAA (produced by some algae blooms and occasionally present in seafood). It closely resembles the amino acid L-serine, and can get misincorporated into proteins in our body, potentially causing this neuro-degenerative illness. An experimental treatment giving patients L-serine so that it substitutes back in place of the BMAA has shown some promise in tests.
This is rare because all Earth life uses the same biology based on a similar chemistry. But perhaps in a collision of biospheres, this sort of thing could become commonplace?
For many more examples see Many microbes harmful to humans are not "keyed to their hosts" in Touch Mars?
So, this could go either way. Or indeed, both ways, that some Earth microbes make some Mars lifeforms extinct, while other Mars lifeforms make some Earth life extinct, and other lifeforms, while not making each other extinct, severely degrade the microbiome for the other form of life, or even the entire biosphere of a planet, making life harder.
Astrobiologists, when asked if Mars life could impact on our astronauts, or the biosphere of Earth, generally tend to say they think the risk is likely to be low. But not zero. However I think it's important to realize that we have never had a clash of independently evolved biospheres, so we have nothing to compare it to.
In a way they are being asked the impossible, if you try to poll astrobiologists about this. To assess it properly they would need to have experience of many different biospheres. Or, of course, to have the opportunity to study Mars life first, before they answer the question.
NO WE CAN'T EXPECT TO DISTINGUISH MARS MICROBES BY SEQUENCING THEM
If all Mars life is derived from Earth life, or the other way around, so that we are distant "cousins, and if our last common ancestor is late enough in evolution so that it all uses the same internal machinery as Earth life does, again there are many issues involved in introducing new Earth microbes to Mars.
You often hear this argument, which I think derives from Robert Zubrin, that it is no problem. The idea is that we will be able to tell if a species comes from Mars or Earth by gene sequencing.
Well to start with, gene sequencing is hardly trivial. We'd like to be able to test to see if there is life there just by putting some dust into a nutrient solution and seeing if it metabolizes. For instance, if it only eats food in one symmetry and doesn't eat the mirror symmetry food (as is the case for all Earth life), that would be a good sign that we had found Mars life already, or some extraordinarily elaborate chemistry not present on Earth. Or we look for amino acids all with the same symmetry. Or more dramatically, we might look at it with a microscope and see if it swims about. There are many tests we can do, and some of them, or a combination of several, could establish beyond question, that there is native life on Mars, if not contaminated with Earth microbes.
But if Earth microbes have got there first, almost none of those tests will do. Even if we spot a microbe purposefully swimming around with our microscope, flagella waving and undoubtedly alive, it will prove nothing. We have only one way to search for Mars life and that is, to look for DNA and sequence it, and test to see it is from Earth or not. Or we try to find some other chemical that may be produced by Mars life and not Earth originated. We are no longer looking for biosignatures, but for "mars life signatures".
They make it sound easy. But even a DNA sequence is hardly a sure fire test. Of an estimated one trillion microbial species on Earth, only 100,000 have classified sequences. That makes it only 0.00001% of all microbial species on Earth that have been sequenced to date. Then, of that 0.00001%,, 90% can't be cultivated in the lab, and are the result of sequencing a single isolated cell using new techniques which reached maturity around 2013. See Largest ever analysis of microbial data (May 2016).
From this you can see that if we find a microbe on Mars that is not in our list of sequenced Earth microbes it will tell us nothing about whether it is from Earth or Mars. There are entire branches of the tree of life, deeply branched, that are only known by a few fragments of DNA, with no cultivable species yet.
To complicate it further, then microbes can swap DNA sequences via Gene Transfer Agents (GTAs) very readily, many of them overnight in sea water. This is a natural process of lateral gene transfer that is so ancient that not only can a fungus transfer capabilities to an aphid, even the most distantly related microbes can do so too.
If Martian life is based on DNA it can almost certainly transfer capabilities to Earth microbes and vice versa in the same way. Before we have a chance to study what is there, we will have Earth microbes that have acquired Martian capabilities and vice versa. There will be no disentangling this mess to find out what happened, given that we don't even know which of the microbes there originated from Earth or Mars in the first place.
Alberto Fairén et al in their "Searching for Life on Mars Before It Is Too Late" suggest that though we couldn't necessarily distinguish individual Martian and Earth microbes, at least, not if they are distant cousins, that we could distinguish a population of Earth microbes from a population of Mars microbes. They suggest that the generation times of Earth microbes on Mars are likely to be very slow, by analogy with their behaviour in Antarctic conditions, and so would take 50 years to cover a small patch of Mars of one square kilometer with a density of 5000 cells per gram. In detail:
"A more realistic example would be the generation time of 2.5 years for bacteria exposed to temporal freeze–thaw cycles in the permanent ice covers of Antarctic lakes. Assuming such an optimal environmental situation for Mars, a contamination of 100 metabolically active cells would require 50 years to produce a cell density of about 5000 cells/g in a square kilometer"
"Furthermore, we have an excellent control with which to monitor the potential contamination of Mars: sequencing the microbes found in the clean spacecraft assembly rooms. Any sequence identical or highly similar to those found on a martian sample would indicate very likely contamination and should be discarded as being indigenous to Mars.
"All the facts described above strongly suggest that if we ever find microorganisms on Mars, we will be knowledgeable enough to distinguish martian (exobiota) from terrestrial (contamination) life. That of course applies only for a short time span in the future, while the terrestrial biological contamination of Mars (if any) remains contained (close to our spacecraft) and known (present in our clean rooms) and therefore manageable. Human missions will change the name of that game forever."
Their idea is that we examine the habitats on Mars, sequence the genomes, and if the resulting population closely resembles the microbe assemblies from clean rooms on Earth, we discard it as contamination, and look again. In that way, they hope to be able to find the remaining genuine Martian populations that have not yet been contaminated by Earth microbes. They want to do this as quickly as possible before human missions make these studies impossible.
I find their reasoning a bit hard to follow here. First, they suggest Curiosity approaches a potential habitat. But Curiosity is not equipped to detect life and certainly has no DNA sequencer on board, so there would be no way that it, for one, could distinguish between Martian life and Earth contamination. For that matter, it wouldn't be able to detect the Earth microbes either if they remained in small concentrations similar to those in other extreme conditions. All it could do is to detect organics and it would not be able to tell if they came from Martian or Earth life or were just organics brought there from meteorites or comets. It's just not equipped for the job, being designed as a geology rather than an astrobiology explorer. There are many instruments we could send that are up to the task but none of them are on Curiosity.
Then, if we did send a more sophisticated rover with single cell gene sequencers - this is possible using SETG which is already space hardened and the experimenters say could be made ready to fly quickly - how do we tell if it is Earth life or our Martian cousins? They suggest testing to see if there is a deep branching from Earth life. But we often discover new forms of microbes on Earth that were separated from the other branches long ago. Perhaps some of those got to Mars in the past in which case it may belong to families we have on Earth already. But the Earth microbes that get to Mars on our rovers are also, many of them, going to be unstudied unsequenced microbes.
To complicate it all further, any Earth microbes that flourish in the Mars conditions are extremophiles and unusual. The conditions there are so unlike anywhere on Earth, with perchlorate, sulfate and hydrogen peroxide rich brine, battered with ionizing radiation, irradiated with strong UV (if there is any surface exposure), and with daily temperatures cycling through tens of degrees below zero and back to more habitable conditions. The salinity also goes through similar cycles every day. Though we have present day Mars habitability analogue environments that duplicate many of those conditions separately, - we don't really have anything quite like that in all respects on Earth. In particular we don't have the thin atmosphere (which is what leads to many of the other effects indirectly).
Also, there are few places on Earth that are so super-oxygenated as the Mars surface with its hydrogen peroxides and perchlorates - which nevertheless also have significant chemical gradients if you just dig a little below the surface.
Any Earth life that can handle such strange conditions might seem quite alien if we haven't come across it yet in our studies here on Earth. Just the process of selecting the few Earth microbes able to survive in the habitat is likely to produce a community unlike any we have seen before, and could encourage many species of microbes to flourish that occur here in such low numbers they were never noticed before.
As for their idea of sequencing microbes found in spaceship assembly clean rooms - no such census can be complete. Any of billions of species could get into the clean room and onto the rover, and it doesn't have to be one of the most common species that survives all the way to Mars and contaminates the surface. And the conditions in the clean rooms, though extreme, do not resemble the conditions the microbes encounter on Mars. There are many differences and so the populations of microbes that survive on Mars are just going to be ones that are in the intersection of microbes that survive the clean rooms and all the way to Mars with ones that can survive in the new habitats. Again it is possible that rare microbes, never detected in the surveys of the clean rooms, are the ones that proliferate on Mars.
Our microbes on Earth could also take up capabilities from any Martian life by lateral transfer and it could also evolve new capabilities, or unlock genes through gene expression that are rarely needed on Earth. The result could easily seem "Martian" and yet just be introduced Earth life. We might discover this, embarrassingly, months after announcing discovery of Martian life. Perhaps even years after the groundbreaking "discovery", someone spots this "Martian" DNA sequence on Earth in some new microbial survey and we discover that what we thought were new insights about Martian life were just insights into the behaviours of microbe stowaways adapting to the Martian conditions.
If you do somehow find a way to characterize the native Mars life - then so long as it is reasonably similar and DNA based, even as you study them, you are introducing Earth microbes, and these are sharing genes with the life you are studying via lateral transfer. Whatever information you collect during your mission will be the only information available to future scientists for all future generations about these habitats, as they were before you introduced Earth life to them. It is a philosophy of despair it seems to me.
SAD ARTHUR C CLARKE STORY ABOUT FORWARD CONTAMINATION
As I write about these various ways that Mars life could be made extinct by our Earth microbes, I am reminded of a sad science fiction story that I use to help motivate my Touch Mars? book.
Few science fiction authors have tackled the theme of forward contamination of other parts of our solar system by Earth microbes, but there's one poignant sad story, by Arthur C. Clarke, "Before Eden". This story was published in the same year as his more famous classic short story "A Fall of Moondust", in Amazing Stories, June 1961. Back then, though they knew Venus was hot, scientists thought it was still possible that Venus could have water on its surface, perhaps at the top of its mountains.

One of the covers for Arthur C. Clarke's "Before Eden" -a poignant sad story about forward contamination of Venus, published in 1961 at a time when surface life there was still a remote scientific possibility. You can hear the complete story read as an audio book here.
These adventurers are exploring a completely dry Venus, or so they think. Up to then (in the story), everyone thought Venus had no water, and was sterile of life. That was a natural thought, because the temperatures they encountered were always above the boiling point of water. But the heroes of the story are stranded near the not quite so hot South pole, and find mountainous cliffs there. On those mountains they find a dried up waterfall - and then - a lake!
“Yet for all this, it was a miracle—the first free water that men had ever found on Venus. Hutchins was already on his knees, almost in an attitude of prayer. But he was only collecting drops of the precious liquid to examine through his pocket microscope.... He sealed a test tube and placed it in his collecting bag, as tenderly as any prospector who had just found a nugget laced with gold. It might be – it probably was – nothing more than plain water. But it might also be a universe of unknown, living creatures on the first stage of their billion-year journey to intelligence....”
“...What they were watching was a dark tide, a crawling carpet, sweeping slowly but inexorably toward them over the top of the ridge. The moment of sheer, unreasoning panic lasted, mercifully, no more than a few seconds. Garfield’s first terror began to fade as soon as he recognised its cause....”
“… But whatever this tide might be, it was moving too slowly to be a real danger, unless it cut off their line of retreat. Hutchins was staring at it intently through their only pair of binoculars; he was the biologist, and he was holding his ground. No point in making a fool of myself, thought Jerry, by running like a scalded cat, if it isn’t necessary. ‘For heaven’s sake,’ he said at last, when the moving carpet was only a hundred yards away and Hutchins had not uttered a word or stirred a muscle. ‘What is it?’ Hutchins slowly unfroze, like a statue coming to life. ‘Sorry,’ he said. ‘I’d forgotten all about you. It’s a plant, of course. At least, I suppose we’d better call it that.’ ‘But it’s moving! ’ ‘Why should that surprise you? So do terrestrial plants. Ever seen speeded-up movies of ivy in action?’ ‘That still stays in one place – it doesn’t crawl all over the landscape.’ ”
“‘Then what about the plankton plants of the sea? They can swim when they have to.’ Jerry gave up; in any case, the approaching wonder had robbed him of words... ”“... ‘Let’s see how it reacts to light,’ said Hutchins. He switched on his chest lamp, and the green auroral glow was instantly banished by the flood of pure white radiance. Until Man had come to this planet, no white light had ever shone upon the surface of Venus, even by day. As in the seas of Earth, there was only a green twilight, deepening slowly to utter darkness. The transformation was so stunning that neither man could check a cry of astonishment. Gone in a flash was the deep, sombre black of the thickpiled velvet carpet at their feet. Instead, as far as their lights carried, lay a blazing pattern of glorious, vivid reds, laced with streaks of gold. No Persian prince could ever have commanded so opulent a tapestry from his weavers, yet this was the accidental product of biological forces. Indeed, until they had switched on their floods, these superb colours had not even existed, and they would vanish once more when the alien light of Earth ceased to conjure them into being...”
“...For the first time, as they relaxed inside their tiny plastic hemisphere, the true wonder and importance of the discovery forced itself upon their minds. This world around them was no longer the same; Venus was no longer dead – it had joined Earth and Mars. For life called to life, across the gulfs of space. Everything that grew or moved upon the face of any planet was a portent, a promise that Man was not alone in this universe of blazing suns and swirling nebulae. If as yet he had found no companions with whom he could speak, that was only to be expected, for the lightyears and the ages still stretched before him, waiting to be explored. Meanwhile, he must guard and cherish the life he found, whether it be upon Earth or Mars or Venus. So Graham Hutchins, the happiest biologist in the solar system, told himself as he helped Garfield collect their refuse and seal it into a plastic disposal bag. When they deflated the tent and started on the homeward journey, there was no sign of the creature they had been examining. That was just as well; they might have been tempted to linger for more experiments, and already it was getting uncomfortably close to their deadline. No matter; in a few months they would be back with a team of assistants, far more adequately equipped and with the eyes of the world upon them. Evolution had laboured for a billion years to make this meeting possible; it could wait a little longer.”
“...For a while nothing moved in the greenly glimmering, fog-bound landscape; it was deserted by man and crimson carpet alike. Then, flowing over the wind-carved hills, the creature reappeared. Or perhaps it was another of the same strange species; no one would ever know. It flowed past the little cairn of stones where Hutchins and Garfield had buried their wastes. And then it stopped. It was not puzzled, for it had no mind. But the chemical urges that drove it relentlessly over the polar plateau were crying: Here, here! Somewhere close at hand was the most precious of all the foods it needed – phosphorous, the element without which the spark of life could never ignite...”
" ... And then it feasted, on food more concentrated than any it had ever known. It absorbed the carbohydrates and the proteins and the phosphates, the nicotine from the cigarette ends, the cellulose from the paper cups and spoons. All these it broke down and assimilated into its strange body, without difficulty and without harm. Likewise it absorbed a whole microcosm of living creatures—the bacteria and viruses which, on an older planet, had evolved into a thousand deadly strains. Though only a very few could survive in this heat and this atmosphere, they were sufficient. As the carpet crawled back to the lake, it carried contagion to all its world. Even as the Morning Star set its course for her distant home, Venus was dying. The films and photographs and specimens that Hutchins was carrying in triumph were more precious even than he knew. They were the only record that would ever exist of life’s third attempt to gain a foothold in the solar system. Beneath the clouds of Venus, the story of Creation was ended.”
How sad it would be if future explorers on Mars get glimpses of early forms of life there, and then they go extinct soon after they are discovered. Or indeed, even before, maybe they are extinct before anyone finds them.
These astrobiologists, feeling that humans on Mars are inevitable and that there is nothing to do about it, are suggesting that we do what the science fiction explorers did in Arthur C. Clarke's book. However, they propose to do it, not by accident, but as a matter of policy. They envision Martian life inevitably getting taken over by Earth microbes or mixed with it inextricably, and propose exploring it in a way they know is not ideal for astrobiology, because it is the only way to get some good astrobiology done before it is too late.
This is tragic, in my view. And if there was more public awareness of the perspectives of astrobiologists, and the various insights from the planetary protection officers, and of the need for protection of Mars from Earth microbes, I don't think this would be necessary.
PUBLIC OPINION IS CHANGING
I do think the situation is slowly changing, Even in the last few years. Just a couple of years ago I'd say things like this and many people would respond, especially colonization enthusiasts: "Are you joking!" They thought it inconceivable that we'd send humans all the way to Mars orbit, orbit it and not land, just to protect native life on the planet.
But there is increasing awareness of these issues, and I hope that I and others who are blogging about it are helping to get this into public view, and to get this debated and aired widely before it is too late.
I find in discussions with the public, that there is a great deal of support for planetary protection and for valuing native ET microbes on Mars. They just have to have it explained to them carefully.
It helps a lot that the message can be a positive one for human spaceflight, emphasizing the value of humans on the Moon and many other places in the solar system, including humans exploring Mars via telepresence - just not on the surface of Mars, or at least not quite yet.
HIGH VALUE OF AN UNINHABITED HABITABLE WORLD FOR SCIENCE
Even if there are habitats there with no life at all, and no Earth life ever got to Mars, that also is amazingly interesting. What happens to a terrestrial planet with no life on it, but organics and habitability, after a billion years?
Mars may be our only chance to study such a situation for many light years distance in any direction. If we blow this chance, we won't have the opportunity to study it again for generations into the future, not in this detail. Not even if we manage interstellar flybys of other planetary systems at some time in the future. The earliest we could expect to get data back even from a flyby of another star, never mind a robotic lander on one of its planets, is probably the end of this century. To study such a planet close up, to the detail we can do with our current robotic missions to Mars from Earth, is probably not something we can do for many centuries.
What happens on a habitable world with no life for billions of years? Do you get self replicating chemicals but no life? Structures that look like cells and maybe even have some kind of metabolism but don't replicate exactly? Giant organic crystals through Ostwald ripening? Nothing even slightly resembling life? This may be our only chance to find out. It could tell us a lot about what happened in the early pre-biotic stages before there was any life, but with millions of years worth of chemical reactions continuing beyond the conditions we can reproduce in laboratory experiments.
At least, it's our only chance until we can travel to other stars.
If there are habitats for Earth microbes at all on Mars, then that means there are habitats that our microbes will change. There will be things we could learn that will be lost by introducing Earth life there before we have an opportunity to study them. And until we know what is there, we simply have no way of knowing what we could lose.
Should we not find out what is there right now, before we decide whether it is okay to lose it?
IF WE CAN'T SEND STERILE ROVERS TO EXPLORE MARS "SPECIAL REGIONS" RIGHT AWAY - OUR FIRST PRIORITY IS TO DESIGN AND MAKE THEM
If we make this decision to continue to protect Mars from forward contamination by Earth microbes and we find that we can't sterilize our spacecraft adequately to visit the special regions with potential habitats - or that the only way to do it is too expensive right now - well, we can wait until we do have the technology. Not just wait idly, but actively develop it. The Russians, drilling into the ice above Lake Vostok in Antarctica, stopped just a few meters short of the lake. They decided that it has probably been cut off from the surface for millions of years, so they just left it like that, while they decided what to do about the last few meters, and how they could do it without contaminating the lake with their drilling fluids and with microbes in the fluids.
Well it's similar with Mars. Do as the Russians did with lake Vostok. Not throw up our hands and say
"We don't have the technology, so, tough, we'll just rush in anyway and if we mess things up, so be it, at least we tried".
It would be so sad to do that, and then find that the native Mars life was made extinct by rushing, when a few more years of patience would have meant we could have learnt all about it.
MARS LIFE FOUND THEN LOST - "FUTURE POSSIBLE NEWS" STORY
Imagine how tragic it would be to have found direct evidence that there was life there up to just before we sent our rover? Or even, to detect it with a rover experiment but to observe the Earth microbes taking over the habitat before your eyes as you study it? This was the thought that lead to that "Fake Future News" story that opens this article.
Your first test finds some alien biology, e.g. DNA with an extra base, or a chemical in abundance, not usual in meteorites and not found in Earth life. Or with the example of an RNA world, even more striking, perhaps it only discovers RNA. cell walls and ribozymes (like ribosomes but much smaller, and made up of fragments of RNA). You find living cells, maybe you can even see them in an optical microscope swimming in the solution (there are proposals to send microscopes to help with the search for life even on robotic missions). You test and there is no DNA there at all, only RNA. Great excitement, you have discovered RNA world cells.
But as you repeat the experiments you begin to find DNA. Then more and more if it. The RNA world signal is getting weaker and weaker until all you can find is evidence of Earth based life in your sample. And the first sample with the exciting results - perhaps that's got contaminated too. Or just that you didn't provide quite the right conditions, they didn't like something in the nutrients you provided, and the life has all died. Most microbes even of Earth life can't be cultured in the laboratory, so it is even likely that it will be impossible to culture RNA world life when first discovered.
You would know for sure that there had been some form of Martian microbe there, you would know that it only had RNA and no DNA, but all you'd know about it is what little data you gathered before it went extinct in that habitat (and probably eventually Mars-wide, as the Earth life is transported in the dust storms). Then, much as for Arthur C. Clarke's scientists on his fictional Venus, the small amount of data you collected in your experiment would be the only evidence of extant RNA world life ever found.
As with Arthur C. Clarke's Venus explorers, those few photos, or maybe video of the microbes swimming would be far more precious than the scientists ever anticipated. They would be pored over by scientists for generations to come to try to glean more evidence and understanding of how the RNA world microbes worked. Those observations made by the first mission to find them might be all we ever learn about them as extant life rather than fossil remains on Mars.
And perhaps there are other square kilometers on Mars where the RNA world will survive for a while. Or maybe this is one of its last few refuges, as in the Venus story, and we don't find the other refuges until it is too late to study the lifeforms before they are extinct. Some of the potential habitats on Mars are very localized
How awful that would be.
WHAT IF WE HAVE THE TECHNOLOGY FOR 100% STERILE ROVERS?
The current planetary protection rules are that you have to have sterilization equivalent to that used for Viking on any spacecraft, or part of a spacecraft, that encounters a potential habitat on Mars.
This means a pre-launch bioload of 500 cultivable spores on the entire spacecraft and so about a hundred times that, around 50,000 spores or dormant microbes in total. That would be reduced further during the journey out and when landing on Mars, and through the surface conditions such as the UV. It's based on probabilities and the idea is to reduce the risk of contaminating Mars to a minimum.
But what if we have the technology to make 100% sterile rovers?
Well actually, it is possible, it's just more expensive. And not as a far future possibility with many engineering challenges to overcome. It is already possible to make 100% sterile landers in principle. We already have all the pieces in place; it's like a jigsaw puzzle ready to be assembled. There's a proposal for a 100% sterile cryobot that we can send to Europa for instance. That is by Brian Wilcox who is working on a 100% sterile probe to descend into the Europan ocean. It would have vacuum insulation like a thermos flask, a blade that cuts ice chips that the body then melts and analysed. It would be heated to over 900 °F (500 °C) during its cruise to Europa which would not only kills microbes but also decomposes organics that would confuse the results.
Vacuum insulated probe for Europa (screenshot from this YouTube video) - it doesn't heat the ice directly. Instead a blade at the tip cuts the ice into chips which the probe then melts and analyses. The probe would be heated to over 900 °F (500 °C) throughout the cruise out to Europa. It uses plutonium 238 for the melting - and so, presumably for its power source too, so there is no problem with batteries vulnerable to heating.
He describes it in a paper here (abstract, the paper itself is behind a paywall).
It's just the probe that's sterile here, not the lander. But combine that with ideas for a Venus lander and we may be getting close to a 100% sterile complete system.
As a result of research into high temperature components for use on Earth and for Venus too, we have all the components needed to build such a machine that is able to survive months of the voyage out to Europa at 500 C, so that the entire apparatus can be heated as a unit. No Earth life could survive that.
We could even remove the organics with CO2 snow. And a lot of progress has been made towards a rover that can drive over the Venus surface, again, in conditions that would sterilize Earth life. If we made it top priority I think our brilliant engineers could figure out a way to send 100% sterile rovers to Mars within a decade probably, if we already have one on the drawing board for Europa.
See also these sections in my online Touch Mars? book.
- Design change suggestions that could make a lander close to 100% sterile
- Can we achieve 100% sterile electronics for an Europa, Enceladus, Ceres, or Mars lander?
The first such rover is bound to be expensive to design, and test, and prove it works. But it would then give us the tools and experience we need to make any number of such rovers at far less cost. And then send them to any of the habitats on Mars, also with appropriate modifications, to explore Europa, Enceladus etc. What a huge difference it would make to have 100% sterile landers so that we don't need to be concerned about contaminating the places we visit with Earth microbes!
Once we develop the technology we will be able to use it to explore throughout the solar system anywhere we are searching for astrobiology. And we will be able to do that without any more concerns about whether microbes introduced on our instruments will impact on the potential habitats we are studying.
This was not possible in the 1970s when current planetary protection guidelines were drawn up. It was a case of either accept a percentage chance of contamination Mars, even if it was only 0.1% over the lifetime of the expected exploration period - or not to send our rovers there at all.
But now we do have a choice.
WHAT IF WE HAVE ALREADY CONTAMINATED MARS?
It seems possible that we haven't contaminated Mars yet, even likely that we haven't .For sure there are dormant microbes on our spacecraft but they are probably just that, most of them stuck in a crack, hidden from the UV and doing nothing.
However the aim for planetary protection measures for Mars so far has always been to reduce the probability of contaminating Mars. Certainty seemed unattainable and that wasn't the aim. So we should face the possibility, hopefully a very remote one, that, through blind chance, we have contaminated Mars already with Earth life.
If we have contaminated Mars already - suppose, heaven forbid, that the methane plumes were formed by microbes introduced to the Mars subsurface by one of the spacecraft that crashed on Mars or a microbe that somehow got into them? Well - hopefully not. But if they were - still, it's not a case of saying
"Okay we've had it, no point in protecting Mars"
That would be like saying "Okay we've introduced rabbits to Australia so it doesn't matter what else we introduce, wolves, foxes, plants, do what you like as it is already contaminated by rabbits".
That's not how it works. If we have introduced some microbe to Mars accidentally - well the native Mars life may still be there as a shadow biosphere. It may be possible to disentangle what happened and to still learn a lot. If that happened I think exobiologists would be very shocked. And everyone would want to know what happened, what we can do about it, and how to limit the damage.
CHECKING HOW EFFECTIVE OUR PLANETARY PROTECTION MEASURES WERE
One thing that would be great would be to get some in situ data on how effective our measures have been so far. We have been doing planetary protection for our missions to Mars for decades now, but it is all based on hypothesis and ideas, and tests in Earth conditions. We don't yet have a single point of hard data to validate those ideas.
If we are really serious about protecting Mars, I think as a priority we should send a mission to study one of the previous spacecraft we sent there, with astrobiology instruments to search for life.
This will serve several purposes
- It lets us send astrobiology instruments to Mars, knowing that they will find something to study at least, the Earth microbial spores on the lander
- Gives us our first data on how well our planetary protection measures have worked
- Also can be combined with an astrobiology mission to study the region around the spacecraft. We may well find microhabitats there.
I would suggest sending it to study the Phoenix spacecraft. After all Phoenix observed what seemed to be droplets of liquid salty water on its legs, possibly Nilton Renno's droplets forming on salt / ice interfaces. These fell off the spacecraft onto the ground (or at least suddenly vanished from the leg).

Also Phoenix got crushed by the advancing dry ice in winter, as was expected for its location. It was never designed to last the winter as they knew it would get sheets of dry ice form on top of it and break it up.

Phoenix lander crushed by frost - layers of dry ice forming on the solar panel in winter snapped one of them off. It was not expected to last the winter. The right hand image shows it in 2010, two years after the image on the left which shows it after landing, in 2008.
If any of our landers have contaminated Mars, I'd have thought Phoenix was a likely candidate. As usual it was sterilized to high standards, but before Phoenix nobody realized there was any possibility of liquid there. Most of those potential micro habitats are probably either too salty or too cold, but are there any that Earth life could survive in? And are any of those close to where Phoenix lies on the Mars surface? We just don't know.
Gallery_Image_6217.jpg
Jim Young (left) and Jack Farmerie (right) from Lockheed Martin, working on the Phoenix lander science deck under clean room conditions to protect Mars, following planetary protection guidelines. Credit: NASA /JPL/UA/Lockheed Martin.
However nobody back then knew that liquid water could form on the surface in those regions.
The entire polar regions of Mars are now declared a "Special Region" and all modern landers there will need Viking level sterilization for any part of the spacecraft that could potentially contact a microhabitat.
All of this is about as much of a battering any spacecraft there has had except for the crashed ones. We also know where it is exactly, we know we can land there, and we have its own observations of its landing site, which may be useful for comparison studies.
So, has it contaminated the ground around it? We will only have a few months to find out unless our rover can survive the dry ice sheets (which would be fascinating to study in situ). It is now thought to be an astrobiologically interesting region, so we can search for Mars life first at some distance from the lander, then approach it, and examine it for contamination by Earth microbes.
The astrobiologists seem to think that there is a pretty decent chance we haven't contaminated Mars with Earth life, mainly because conditions are so hostile. Even if what we have on Mars is as vulnerable as RNA world cells, still, there is a good chance that it is still there and has not yet been extinguished by Earth microbes. And even in that case, we may be able to reverse what we have done, sterilize the rovers already there, or even remove them from the surface. We would need to develop those 100% sterile landers first of course, or we are just going to make things worse by trying to clear it up. But after that ...
We couldn't eliminate every single dormant spore from the dust. But most Earth microbes wouldn't be able to survive there anyway. Others would be sterilized by the UV, cold, heat, perchlorates or any of the other potentially biocidal factors on the Mars surface. We could go to the sites of crashed or crushed landers (via telepresence from orbit), and check to see if any life has started to spread. If so, it may be that it has not spread far yet and can be sterilized. It's not impossible that we are able to reverse the effects of what we have done so far.
SCIENTIFIC VALUE OF NULL RESULTS FOR ASTROBIOLOGY
I think it's important to realize that a null result is important too. Indeed as we search for life on Mars we may get many null results, in one place after another, as we narrow down the search for life there.
If Curiosity had life detection capabilities, it could answer one question right away, "Did Viking find life or not in the 1970s?"
We have day / night rhythms when we sleep at night and eat during the day. Well microbes do too.
These are called circadian rhythms and these patterns were discovered many years later in the Viking labeled release data. The interesting thing is that they are offset from the temperature variations by two hours, which to an expert on circadian rhythms who spotted this, strongly suggested that these rhythms come from life rather than non life processes. Ordinary chemistry can only explain an offset of about twenty minutes.
More on this in the section Rhythms from Martian sands - what if Viking detected life? in my online and kindle book Touch Mars? Europa? Enceladus? Or a tale of Missteps?
Suppose it comes up with the answer "No"? Then we have our answer to this question that has lead to so much debate for decade. It could also determine what chemistry was involved that caused these apparent circadian rhythms in the nutrients offset by from the temperature variations.
That is how you do science. If you are scared of null results, your progress is going to be very slow. Short of spotting an obvious fossil, or a large lichen or some such, we aren't going to find life on Mars until we send astrobiological instruments there to look for it. And then keep looking, until we have tried all the main proposed habitats, and several times over too. As astrobiology isn't neat like geology. The life can be cryptic, hidden inside rocks and beneath a layer of dust or salt, but it can also be very patchy in extreme environments. In the Atacama desert some gypsum pillars have life and some don't, as a result of just a small change of humidity. Similarly if there are cyanobacteria colonizing beneath the surface of rocks, some will have them, and drill just a centimeter to one side, even on the same rock, and you may miss it.
Most astrobiologists do not expect NASA's sample return mission, starting with Mars 2020, to find life. Eight of them warned in a forthright paper to the decadal survey that they expect it to return samples as ambiguous for their subject as the Mars meteorites we have already. It is likely to find organics, but if it returns those to Earth, there will be the same questions we have with the Mars meteorites we already have. Organics are constantly falling on Mars, brought there by comets and meteorites. It's actually more of a mystery why there aren't more organics there; these infalling organics seem to be destroyed rapidly by surface processes, and the organics found by Curiosity already are thought to be from meteorites.
I cover this in detail in my section: Astrobiologists advocating strongly for an in situ search on Mars first in the book. I go into the papers by Bada et al', by Paige, and by Cockell et al, all arguing that we need an in situ search looking for biosignatures and life itself in situ before we even consider a sample return - at least if the reason to return the sample is for the purposes of astrobiology.
REMOVE THE BIGGEST BOTTLENECK FIRST - WE NEED HIGH BANDWIDTH FOR HUMANS - LET'S DO IT RIGHT NOW
As for the idea that it would be much faster to explore with humans - maybe - but at vastly greater expense and what good is it to be fast if you make what you are looking for extinct in the process?
The biggest bottleneck is not the roundtrip time, as you might think. Our rovers are so slow mainly because of lack of bandwidth at present. Our rovers could be as far away as Pluto or even a distant Kuiper Belt Object and it would make hardly any difference, because with the low bandwidth, they arrange for communications only once a day typically.
In the mid 2020s we'll have 800 gigabytes of information a day, a huge increase, if it goes ahead. We simply have no experience of exploring Mars with such a high bandwidth, and we don't even have this for the Moon. The Russian Lunakhod 2, using 1970s technology traveled as far in months as Opportunity did in years, and Lunakhod 3 (if it had flown) would have been faster still. But we have not tried exploring it with more modern technology for the rover, semiautonomous driving, high bandwidth communications, and the many advances in teleoperation technology.
So when bandwidth is our bottleneck, the first thing to do is to remove that bottleneck. We wouldn't send humans to Mars with the bandwidth we have at present. I think we will be amazed how fast the Moon, and then Mars, can be explored robotically once the technology is fully mature.
As an example, to show how it could potentially make a huge difference - for instance with multi-gigabyte 3D panoramas returned from Mars, and virtual reality technology you'd be able to look closely at any rocks around the rover with the equivalent of a geologist's hand lens just by moving around in the virtual 3d scene the rover returned to Earth. You could look closely at any rock, not by moving the rover, but just by walking up to it in 3D VR and looking at it in the images streamed back from the rover for that day. You could tell the rover to go around a rock and photograph it from all angles, and stream the images back, and within minutes you have a 3D image of that rock that you can zoom into with microscopic detail like examining it with a geologist's hand lens.
The rovers can easily be given vastly more powerful engines and more power for the experiments. Humans on Mars would not be driving around at 100 meters a day. They could explore at tens of kilometers a day like the lunar rovers, or even hundreds of kilometers, do Opportunity's entire journey in less than an hour if you so wished. The main reason we don't do that at present is that there is no incentive with the low bandwidth. If it takes days to do a photographic survey of just one small spot and send the images back to Earth - you get into a situation of diminishing returns by making the robot able to cover more ground, because you'd sacrifice instruments in order to add the capability.
Once we do that it also will be worthwhile to give them more autonomy like a self driving off road vehicle on Earth. For power sources - we can use fuel made from hydrogen feed stock on Mars as for the ideas for human driven rovers there, or we can use large areas of thin film solar panels spread on the surface to charge up batteries. Even the equivalent of the lunar rover batteries would give us plenty of mobility.
Eventually we can have humans in orbit around Mars which will speed it up yet again by adding our ability to make on the spot decisions within seconds. They will also be able to virtually "teleport" from one lander to another on the Mars surface, giving them tasks to do, much like directing the inhabitants in a game of Civilization.
And there is absolutely no urgent need to send humans to the Mars surface. The only thing the hopeful settlers have given as a compelling reason is that we need to be multi-planetary" to safeguard our species.
But if we want to make sure our species survives, we have to look after Earth. If we can't there is no way we can look after the much more harsh Mars. And it makes sense to have a backup in space, but as part of a situation where our priority is to protect and preserve Earth. If you think like that the natural place to do it is the Moon not Mars. And there are many other places we can send humans to in our solar system that don't have planetary protection issues.
I think we shouldn't change the rules to permit colonization enthusiasts to go to Mars as quickly as possible, to the one place in the inner solar system most vulnerable to Earth life.
If Elon Musk proposed to melt a hole into Lake Vostok, the subsurface lake in Antarctica, and drop a sub into it with humans on board and cruise around looking for hydrothermal vents, there would be outrage amongst scientists. They would dearly love to do that but they think it is very important to avoid contamination of the lake with surface microbes.
It would be even more so if he proposed to build a city of a million on the floor of lake Vostok. I think you can argue that a colony beneath the Antarctic ice, in a subglacial lake, would be more feasible in the near term than a city of a million on Mars.
If it matters even for lake Vostok cut off for only a few million years, of course it matters for Mars, and we should make that clear. That needs to be a starting point of planetary protection discussions, clearly and unambiguously recognizing the value of Mars for science, and the potential impact of Earth microbes on the planet.
OUR MICROBES COULD TURN MARS AQUIFERS INTO CEMENT IN THE ANOXIC, POSSIBLY METHANE RICH CONDITIONS THERE
We also have no idea what Earth life would do to Mars, in the unusual conditions there unlike any that we have on Earth - but possibly still habitable to Earth microbes. The previous planetary protection officer, the biologist Cassie Conley gave a simple example to show how we could get an unpleasant surprise if we introduce microbes inadvertently without knowing all the interactions and what they could do there.
Some Earth microbes, in the anoxic conditions on Mars and in the presence of methane (which may well be present there), could form calcite in underground aquifers - so turning them to cement.
"Conley also warns that water contaminated with Earth microbes could pose serious problems if astronauts ever establish a base on Mars. Most current plans call for expeditions that rely on indigenous resources to sustain astronauts and reduce the supplies they would need to haul from Earth."
"What if, for example, an advance mission carried certain types of bacteria known to create calcite when exposed to water? If such bacteria could survive on Mars, Conley says, future explorers prospecting for liquid water instead might find that underground aquifers have been turned into cement."
Going to Mars Could Mess Up the Hunt for Alien Life
In more detail, Mars has almost no oxygen, which changes how microbes behave. What she is talking about there is anaerobic oxidation of methane, which leads to the formation of calcium carbonate in anoxic conditions . It's done by a consortium of methane oxidising and sulfate reducing bacteria. See summary here in wikipedia: Calcite - formation process - which links to this technical paper which goes into more detail.
Calcite - calcium carbonate. In the anoxic conditions on Mars, in presence of methane, a combination of methane oxidizing and sulfate reducing microbes can cause calcite to form and so, basically, could turn underground aquifers on Mars into cement. Cassie Conley’s example of one way that accidentally introduced microbes could have unpredictable effects on Mars.
When it comes to microbes introduced to an unfamiliar planet that behaves differently from Earth, with many differences in the chemistry, atmosphere, environment - any number of unexpected interactions could happen.
Another thing that can happen is that the microbes from Earth mutate on Mars. That's likely in the unusual conditions, not like anything ever encountered on Earth, and the ionizing radiation will increase the mutation rate too; they can also recover hidden capabilities through changes in gene expression. They can also take up capabilities from Mars microorganisms via lateral gene transfer, if it is related, or is unrelated but still uses DNA / RNA. The resulting new pathogens combining traits from Earth and Mars organisms, or mutated in the Mars conditions, could endanger the astronauts too. Quoting from Conley and Rummel's paper
"Given the assumption that there really will be a serious effort to go to Mars with humans and have them do things on the surface, we can posit that human missions will inevitably bring a large population of Earth microbes along with them. We should anticipate, too, that not all of those microbes will always be harmless. If humans are going to contaminate Mars, we also need to be concerned about the possibility that the microbes they carry could endanger the astronauts, both in their native state and if they mutate in the space environment. If Earth life and martian life are related, or if martian life is unrelated but still uses DNA/RNA, then lateral gene transfer is another route for acquiring new (and potentially hazardous) traits. While COSPAR planetary protection policies are principally science-enabling, they have other benefits as well."
(Emphasis mine)
It's not as if Mars is the only place we can send humans to. We have the Moon, the moons of Mars, Venus, Mercury, and if Elon Musk is right about his BFR then within a decade or two we should have access also to Callisto in the Jupiter system and Titan in the Jupiter system to send humans to as well. Callisto has many advantages for humans over Europa as Elon Musk's ice refueling station in the Jupiter system and also for settlement - and is already passed as Category II, similar to the Moon, no problem sending humans there.
We can also build habitats in the asteroid belt, with enough materials there for radiation shielding for a thousand times the surface of Mars, slowly spinning the habitats for artificial gravity, or using two habitats tethered together lazily revolving around their center of gravity. They keep revolving due to angular momentum, and don't need any source of power to keep them going. It's like a bicycle wheel spinning endlessly on frictionless bearings.
Video fly through of a Stanford Torus style space habitat by Uzi Bento
In the future we could have humans fill the solar system right out to Pluto and beyond, and still keep Mars free from Earth microbes if we felt what is there is valuable enough and also vulnerable to Earth microbes.
With thin film mirrors you can get plenty of sunlight for a habitat even well beyond Pluto with much less mass than you need for the habitat to reflect the sunlight into the habitat.
For more on this:
- Asteroid Resources Could Create Space Habs For Trillions; Land Area Of A Thousand Earths
- Value Of Titan As Base For Humans In Saturn System - Surprisingly - Once There - Easier For Settlement Than Mars Or The Moon
Why the big rush to send them to Mars? Of all the places we could send them, why send them to Mars, one of the most vulnerable to contamination by Earth microbes? If we feel it urgent to ensure we have an extra "backup" in space, so urgent we have to do it right now, not wait even two decades, we can do it on the Moon, which has perfect conditions for a seed bank at liquid nitrogen temperatures in the craters of eternal night at the lunar poles, and can be developed into a small caretaker colony and eventually a larger settlement.
Also, for human exploration the Moon is close by, easy to get to (comparatively) but still a huge challenge that will stretch us to the limit. The Apollo astronauts made it seem easy, but it's not. They were test pilots that often made decisions in seconds that avoided disasters that would have killed everyone if they weren't experienced test pilots used to flying new designs of planes that could crash any moment, and often did.
IMPOSSIBILITY OF PLANETARY PROTECTION AFTER A HUMAN CRASH ON MARS
However careful you are with the humans on the surface, however much you can slow down contamination (and everyone agrees it can only be slowed down - after a human landing then our contamination of Mars by Earth microbes is irreversible) - what can you do in the event of a crash landing?
The chance must be rather high. It's an exceptionally dangerous and risky mission for humans to attempt, requiring many complex steps to be done in a few minutes. After a Columbia style re-entry crash, debris would be spread over hundreds, or thousands of square kilometers of the Mars surface.
The debris field for Space Shuttle Columbia, with a debris track around 350 miles long, and about fifty to a hundred miles wide (depending on whether you measure to the most distant debris). An accident, especially if it happened early during the supersonic retropropulsion entry to the Mars atmosphere, could scatter debris over a large area of Mars.
If you send humans there, there is a chance that you are able to control the contamination to some extent and slow it down. But as Elon Musk himself says it is "fun but dangerous". Even with previous unmanned missions, there is still a high chance that the first human mission crashes there, so ending any possibility of even slowing down the inevitable irreversible contamination of Mars with Earth microbes. It's also unlikely that the precursor missions to set up habitats and fuel stations on Mars would be sterilized enough to protect Mars in the event of a crash.
If the human mission was to the vicinity of a region of interest for life, then the chance of contaminating that region even right away after a crash must be high.
So what can we do?
Well to start with, we are all of us together on this, as far as orbital missions around Mars and missions to the Mars moons, which would be likely to come first anyway for safety reasons. This may take a fair while.
SENDING HUMANS TO MARS RIGHT NOW LIKE PADDLING FROM PARIS TO AUSTRALIA IN CANOES - CHRIS HADFIELD'S EXAMPLE
The retired Canadian astronaut Chris Hadfield, former commander of the ISS, interviewed by New Scientist, put it like this in their article "We should live on the moon before a trip to Mars"
"I think ultimately we’ll be living on the moon for a generation before we get to Mars. If the world and the moon were threatened and the only way to preserve our species was to launch from Earth, we could go to Mars with yesterday’s technology, but we would probably kill just about everybody on the way."
"It’s as if you and I were in Paris, paddling around in the Seine in little canoes saying, 'We’ve got boats, we’ve got paddles, let’s go to Australia!' Australia? We can barely cross the English Channel. We’re sort of in that boat in space exploration right now. A journey to Mars is conceivable but it’s still a lot further away than most people think."
Elon Musk has big plans for his BFR. Perhaps that might change things, but on the other hand - we are at only the early stages of life support systems. The ISS has had numerous life support issues which were only fixed due to resupply from Earth. See this list of some of them. None were immediately dangerous, and some were relatively minor but some of them would have been fatal on a timescale of months.
The logistic figures support the idea that what we have now may be reliable enough for a Mars mission. It's hard to be sure though, with a sample size of 1. In a recent evaluation the conclusion is:
"With several readily apparent exceptions, WRS [water recovery system] and OGS [oxygen generation system] equipment has been shown to be capable of achieving operational lifetimes on the order of those needed to support such missions. It is important to note, however, that the sample size represented by the fleet of WRS and OGS ORUs (Orbital Replacement Units) that have been used in operational service remains very small (sample size of 1 in most cases) and that statistical reliability predictions cannot be supported by this data alone. Furthermore, other challenges likely to be faced in developing Mars transit and surface vehicles, such as mass and volume constraints, water and oxygen loop closure needed to support mission scenarios, dormancy management, equipment reparability, etc., also will need to be considered as part of an integrated Mars exploration mission and vehicle design. But in terms of highlighting first-order trends and focus areas needing improvements, the daily operation of the ISS WRS and OGS is providing an invaluable first step towards human Mars exploration. "
Even SpaceX do come up with a supremely reliable Mars capable spacecraft with the BFR, I think you would need to start with a "shake down" cruise in LEO testing the actual systems you would use for the mission for a similar duration mission in LEO with no resupply from Earth. Or for a more interesting mission perhaps -you can send it to the far side of the Moon, to L2. After all it is going to get no resupply from Earth during the entire mission to Mars. So, leave the BFR at the far side of the Moon, and they can explore the surface of the Moon via telepresence during their two years simulated Mars expedition. With Earth hidden behind the Moon it would have some resemblances to orbiting a distant planet. They could also introduce simulated radio time lag (which could be overridden in an emergency). Yet they can get back to Earth in a couple of days if something goes badly wrong.
So for practical reasons also Mars may be a step too far for humans. And when we go there eventually, we can have humans in orbit or on its moons, an exciting mission, to explore it via telepresence. All of that is compatible with planetary protection.
So we are together this far, all of us can be on the same page.
Indeed the BFR could make for an extremely spacious orbiting station for exploring Mars. As for gravity - the BFR could spin via a tether spin arrangement with a second BFR to generate artificial gravity throughout the journey to Mars and while in orbit around it. Tether technology is mature enough so that this is feasible no matter how slow the spin needs to be. The relative velocity of the two spinning craft would only be meters per second, not kilometers per second, so it is easy for them to dock with each other again in the case of a tether break, though you'd need to make sure the orbit was designed so that a tether break would not lead one of them to go careening into Mars.
If it had rather fewer people, 20 per BFR instead of 100, then his BFR could be spacious enough to grow sufficient crops to sustain the crew indefinitely, for years on end if necessary, providing nearly all their food and oxygen. Just inside the BFR, using solar collectors and light tubes for the light for the crops. I talk about this a bit more in my Value Of Titan As Base For Humans In Saturn System - Surprisingly - Once There - Easier For Settlement Than Mars Or The Moon
Once you can do that, you then open out the solar system. By sending a mission to orbit Mars without resupply for several years, and Venus also, those then would be "shake down cruises" to go further afield in multi-year voyages to Mercury, Jupiter and even further afield.
Perhaps, by then, we have managed to send astrobiological instruments to Mars - either before- or ones for them to use to study the planet from orbit with their first orbital missions there. If so, any of them could discover present day life on Mars at any time. As soon as that happens, the whole thing may begin to become much clearer to us all, as we begin to learn about Mars life, what its capabilities are, and vulnerabilities, and whether it is related to us.
I think the answer to Elon Musk's plans to send colonists to Mars is not to restrict ambitions but to be even more ambitious. Look further afield to Venus, Mercury, Jupiter, Saturn, eventually Triton, Pluto and beyond. But to keep Mars protected for now as part of an open future, with an initial phase of exploring Mars vigorously from orbit and using robots also operated from Earth. It's a case of being more ambitious, rather than less, and keeping our future options open, until we know more about what we are dealing with on Mars, which may or may not be compatible with us, if our biospheres collide. An affirmation:
"Yes, we can do this, we can explore Mars from orbit, and we don't need to introduce Earth microbes or risk getting our astronauts exposed to Mars life. We are in control of our own destiny and can decide what to do for ourselves. We are thinking beings and we can use foresight and insight to plan our futures".
There is so much we can do on the Moon. For that matter in many ways it is a far easier place to go, to do our first experiments in human settlement in the solar system than Mars.
- No dust storms
- the hard vacuum simplifies many things (e.g. can make solar panels by vacuum deposition in situ)
- the dust is more easily managed in a windless environment and has nanophase pure iron mixed into it so that it can be sintered to glass easily with a microwave
- sunlight 24/7 nearly year round at the poles
- Double the sunlight levels of Mars
- You can see Earth in the sky, nearly four times as wide as our Moon is from Earth.
- large lunar caves that may be so big in the lunar gravity that you can fit a city inside, sheltered from solar storms, cosmic radiation and even fairly large meteorites too.
- far more of an economic case, because it is so close and accessible compared to Mars, for tourism, and various suggestions for exports including potential for platinum from iron meteorite impacts, and ice at the poles
- And it is huge too, continent sized, much to explore, much not yet known
- Natural cryogenic conditions at the poles below liquid nitrogen temperatures, also suitable for superconductors and passively cooled infrared telescopes
- Craters ideal for huge Arecibo style radio telescopes
- Far side permanently shielded from radio interference from Earth
It is of interest to astrobiology too, because, just as we have Mars meteorites on Earth, the Moon must have them too. But not weathered, still in their original state. Not only that, in the cold traps at the lunar poles, meteorites will preserve organics not just from recent impacts on Mars but right back to meteorites that got here after huge impacts into the primordial Martian oceans. Any Mars meteorites from that time on Earth are long lost - the ones we have got here in the last few thousand years.
We may find meteorites from Venus too, possibly with traces of venusian microbes in them, if it ever had a thin enough atmosphere. Some think its present day thick atmosphere is only a few hundred million years old,and may have remained habitable to life on its surface until as recently as 715 million years ago. Its current atmosphere may have formed after a global upwelling of a vast magma superplume (something that can't happen on Earth because of the constant continental drift).
Also we can be certain that it will have meteorites from early Earth, after impacts here billions of years ago. They will be preserved there complete with the organics and DNA etc, kept at temperatures of liquid nitrogen and below for billions of years from right back to soon after life first started to appear on Earth.
Although it hasn't had a lot of attention, potentially the Moon might be as much of a treasure trove for the study of past life as Mars. Maybe more so in some ways, as it may take a fair bit of exploration on Mars before we find the places with the right conditions to preserve past life there for billions of years.
Phobos, the innermost moon of Mars is also expected to be a treasure trove of meteorites from early Mars. Without the cryogenic conditions, but meteorites preserved after a short flight path and in great abundance from the entire history of Mars, or at least, since Phobos formed.
I cover this in detail in these sections of my Touch Mars? book:
As humans we are not just the biosphere's way of getting into space. We are also our biosphere's "noosphere" (a term from Theillard de Chardin). We are our biosphere's way of thinking about the future and anticipating consequences and avoiding consequences that could be disastrous or unfortunate for it and for us. We can be its way of protecting itself from asteroid impacts too and anything else that threatens our Earth from space.
It is within our capability to ensure that we have more than a brief window of time, and that if necessary we can take as long as is required to find out what is on Mars and how Earth microbes will interact with it and how it will interact with Earth life and our astronauts, before sending anyone there.
ELON MUSK ON WHAT TO DO IF WE FIND LIFE ON MARS
Here he answers a question on this topic, in the 2015 AGU conference in San Francisco, 30 minutes into this video:
Q. "I am Jim Crawl from Arizona State University. I was listening to doctor Chris McKay, another advocate of humans to Mars, and he was talking about when we do go to Mars and if we find life either currently there or extinct, we should consider removing human presence so that we can allow that other life to thrive. I was wondering what your thoughts on that were. "
His answer:
A. "Well it really doesn't seem like there is any life on Mars, on the surface at least, we are not seeing any sign of that. If we do find some sign of it, then for sure we need to understand what it is and try to ensure that we don't extinguish it, that's important. But I think the reality is that there isn't any life on the surface of Mars. There may be microbial life deep underground, where it is shielded from radiation and the cold. So that's a possibility but in that case I think anything we do on the surface is really not going to have a big impact on the subterranean life."
If astrobiologists and others were to make it crystal clear to him that there is a diversity of views on this topic and that there remains a definite possibility that Earth microbes could make Mars life extinct and that we can't rule this out, yet, I think he'd be concerned himself also. He does have an interest in science.
WE HAVE NOT YET STARTED ON A PROPER BIOLOGICAL EXPLORATION OF MARS
It's not through lack of interest. First, Mars is vast. It is a planet with surface area as large as all the continents of Earth put together.
It is difficult to visit also. Half the missions there have crashed. Many others are interested, not just the US. Russia has sent many attemped landers to Mars, none successful for more than a few moments. The UK sent the Huyguens lander and it nearly succeeded but one of its solar panels failed to open, as we found out only years later from orbital photos and it never “phoned back”.
ESA’s Schiaperelli lander also crashed. And nobody else has had the technology yet to attempt a landing on Mars. With its thin atmosphere but high gravity (compared to the Moon), it’s the hardest place to land in the inner solar system.
So far we have had only these successful landers:
- Viking 1 and 2 - the first and only astrobiological missions. None of the others have attempted to search for life there. They produced ambiguous results that are discussed to this day -due to the bizarre and totally unexpected chemistry of the Martian soil interfering with the experiments. We now know the problem was that they are rich in perchlorates which are very unusual on Earth. They were stationary landers and the places they landed we now know to be not very habitable.
- Pathfinder + mini rover Sojourner - a geology mission looking at rocks in one small patch of Mars, the “rock nest”.
- Phoenix. Polar lander. Found evidence of water present on the surface in present day Mars both from droplets on its legs and isotope evidence in the atmosphere. This is now thought to be the only one of all these missions to have been sent to a region with a decent possibility of present day life - though that was not realized at the time. However it was not able to move and had no life detection capabilities.
- Opportunity and Spirit - rovers. Spirit got stuck in the sand eventually. Opportunity is still running. It’s traveled over 10 km. Found salts, minerals that could only form in water, the "blueberries" that on Earth are the product of biological activity but we don't know on Mars, and many other things. But had no life detection instruments, past or present.
- Curiosity - still exploring - got good evidence that Mars in the past had habitable lakes in Gale crater - and found organics probably from meteorites.
So - only two astrobiology missions, Vikings 1 and 2 in the 1970s.
Meanwhile our orbiters have found numerous possible sites to search for present day life.
None of these have been visited by either a lander or a rover.
Nor have we yet sent any spacecraft to the surface able to drill more than a small way into a rock. For past life we need to drill meters to have a decent chance of finding it (life on or near the surface has to be metabolizing - even if only slowly - in order to repair its DNA over time periods of thousands of years)..
SUGGESTIONS FOR LIFE, DEEP BELOW THE SURFACE, BUT ON THE SURFACE AS WELL
There are many suggestions now for habitats not just at the base of the regolith, but on the surface or in the top cm or so of the soil as well. There is an almost bewildering variety of possible habitats for surface, near surface and subsurface life. None confirmed but many to be investigated. Here are some of them - the links take you to the section of my online Touch Mars? book.
- Nilton Renno's droplets that form where salt touches ice - why did he call a droplet of salty water on Mars "a swimming pool for a bacteria"?
- Recurring Slope Lineae
- Lichens and cyanobacteria able to take in water vapour directly from the 100% night time humidity of the Mars atmosphere
- Liquid brines beneath the surface of sand dunes at night - beneath the sand that Curiosity drives over - that one was reported as uninhabitable but Nilton Renno was not so sure, biofilms might make it habitable
- Transgressing sand dunes bioreactor
- Desert varnish
- Sun warmed dust grains embedded in ice
- Southern hemisphere flow-like features - these may involve fresh water!
- Methane plumes on Mars and the possibility of water deep below the surface in its hydrosphere (could be surface or subsurface)
- Porous basalt
- Two ways Curiosity's methane spikes could be generated in the shallow subsurface (centimeters deep at most)
- Ice covered lakes habitable for thousands of years after large impacts
- Ice covered lakes from volcanic activity
(the ice covered lakes from impacts and eruptions here are a remote possibility for the present day - but there have been searches of the polar ice caps for radar signals of water deep below the ice - the interesting thing is that once formed, they would stay liquid indefinitely, insulated by the ice above and warmed by the interior heat of Mars below)
- Possibility of geological hot spots in present day Mars
- Life in ice towers hiding volcanic vents
Also see Modern Mars Habitability in Wikipedia (one of my contributions to the encyclopedia)
None of these have been visited by either a lander or a rover.
Also they are cryptic habitats except for the lichens and cyanobacteria using the night time humidity. Any life in these habitats would be expected to be invisible from orbit. The lichens and cyanobacteria would be likely to be hard to detect from orbit too, as if they behave as they do in Antarctica they would huddle in partial shade in cracks in the rocks, and would probably do it even more so in the harsh UV of the Mars surface.
DO WE NEED TO DRILL FOR LIFE? WHY IONIZING RADIATION IS NOT A LIMITATION FOR PRESENT DAY NON DORMANT LIFE
The surface radiation is sterilizing for microbes that are dormant for hundreds of thousands of years, which is not long enough for them to survive on the surface since last time it was warm enough for liquid water on the surface. That's why most astrobiologists, until recently, would say that any viable life on Mars has to be at least a few meters below the surface.
However, starting with Phoenix and the high resolution orbital images, we have found many possible ways that liquid water can form in the top few cms.
So, many of the proposed habitats would permit microbes to metabolize right now. Some radioresistant microbes on Earth such as Chroococcidiopsis can repair damage from ionizing radiation within hours. Even double breaks right through the DNA strand, using other copies of the same strand to fix them - it's remarkable. They would have no trouble surviving in the conditions there even if metabolizing so slowly that the cells have individual lifetimes of millennia.
On shorter timescales the radiation is no problem at all. It's roughly equivalent to the radiation levels inside the ISS. Microbes can handle that no trouble at all, even humans can, with a slightly increased risk of cancer.
But the damage is exponential. For instance, suppose that the number of viable microbes in a particular species is reduced to a tenth in 10,000 years. Well within 20,000 years you have only a hundredth of the original cells, after 30,000 years only a thousandth and so on. Within 100,000 years you have only 1 in 10 billion of the original cells surviving, within 200,000 it is only 1 in 100 billion billion or 1 in 1020 - and after a million years you can see there is essentially no chance of survival (1 chance in 10100 )
When it comes to drilling for past life, then over billions of years, the cells are not only killed, but most of the organics are decomposed to carbon dioxide, water, methane etc. For a reasonable signal of past life you need to drill deep, several meters. But most of the organics you find will still probably be degraded beyond recognition or not derived from life originally anyway. That's why the astrobiologists say it is so important to search for life in situ, so you can test in many different locations, at different depths. It is just impractical to return all those samples to Earth for testing here.
ExoMars will be the first to drill for life. For some reason NASA haven't been interested - though the Beagle also had a robotic mole so ESA / UK in that case have a long term interest. NASA are sending the InSight lander but although its heat flow probe will drill down for five meters, it won't be drilling to search for past or present day life.
Deep below the surface any present day life would be dormant, unless you are lucky enough to drill into a geological hot spot (none yet known on Mars). But it might be revivable and stay dormant for millions of years if you dig deep enough so that it is protected from surface cosmic radiation. So for viable present day life, it's likely to be either
- as active living cells in surface or near surface layers where it has access to liquid water in some form including brines, or uses the night time humidity enabling it to metabolize and repair its DNA and eventually reproduce
- in geological hot spots - none have been found despite an extensive search - but Mars is still geologically active with volcanic eruptions in the last few million years, and some hypothesize that the RSL's may lie on top of geological hot spots - and possibly the methane plumes could come from geological hot spots too. They may just be hard to spot or deep below the surface.
- or lying dormant some meters below the surface
- or very deep down in the hydrosphere.
VIEWS OF ASTROBIOLOGISTS ON WHETHER THERE IS LIFE ON OR NEAR THE MARS SURFACE
There are plenty who do say it is possible that there's life there close to the surface of Mars in their papers. I summarize their views in the section "Views on the possibility of present day life on or near the surface" in the article Modern Mars Habitability
The main views I summarize there as (removed the footnotes):
- Unlikely - these authors cite the inability of microbes to survive dormancy on the surface between periods when the atmosphere is thicker, due to ionizing radiation, the ephemeral nature of surface habitats, low temperatures, or low relative humidity, and the difficulty of colonization in surface conditions of high UV
- Possible, recolonized from below, these point out the ability of micro-organisms to repair damage by ionizing radiation and capability to remain dormant for up to several million years in the deep subsurface, suggesting that these short lived surface habitats, such as the Recurring Slope Lineae, could be recolonized from the subsurface.
- Possible, open question if it proliferates on the surface these are investigating the possibility with experiments in simulated Mars conditions, theoretical models and study of the observations from Mars, and treat it as an open question for now, whether the present day surface and near sub surface is habitable. .
- Likely Some researchers, particularly the researchers at DLR consider that their experiments have already shown a high likelihood that the surface of Mars is habitable, for some lichens and cyanobacteria, taking advantage of the night time humidity, and even in equatorial regions such as Gale crater.[.
- Already detected on the surface A small minority of authors believe that their reanalysis of the Viking Labeled Release experiments already indicates presence of life on present day Mars
There is greater agreement on deep subsurface habitats since conditions there may be similar to Earth conditions. They would be protected from UV, cosmic radiation, and the low pressure of the atmosphere, and water activity would be likely to be similar to Earth. For instance the deep hydrosphere (if it exists), or temporary lakes that form after impacts or volcanic eruptions, seem likely to be habitable, by analogy with similar habitats on Earth.
VULNERABILITY OF THE DEEP HYDROSPHERE AND GEOTHERMAL HOT SPOTS TO SURFACE MICROBES
Many seem to think that any life deep below the surface would be immune to disturbance from the surface, as Elon Musk said in his quote. Perhaps some of it is. But Mars is a little different from Earth. Even here there's some contact. On Mars, many microbes in the deep hydrosphere or in geothermal hot spots and caves could still be vulnerable to spores scattered in the dust after a crash of a human occupied spacecraft on Mars.
One thing that makes this more likely is the way that the entire surface of Mars is "gardened" by meteorites on a planet with almost no atmosphere, ten times the meteorite flux of Earth, and no continental drift to recycle the surface and reform rocks. The ground is thought to be permeable to considerable depths over much of Mars. Even on Earth you get surface seeps from methane from deep subsurface reservoirs of gas.
Then, 90% of the rocks in the vicinity of Viking 2's landing consisted of porous basalt, riddled with holes. If there's some source of hydrogen, for instance, it could be very habitable. Basalt has has the chemical elements needed to support a million cells per gram (limiting factor is phosphorus) and there are likely to be perchlorates, nitrates and sulfates from the surface to increase its fertility for life. See this paper.
The methane plumes that Curiosity detected, if they are confirmed, may well be signs of some communication between the deep subsurface and the surface. If so, then that could mean there is possibility for transfer both ways. That might become not just possible, but likely, if some geothermal hot spot reaches to close to the surface and makes surface brines habitable (one hypothesis for the RSL's).
WHY ABSENCE OF EVIDENCE IS NOT EVIDENCE OF ABSENCE IN THIS PARTICULAR CASE
Part of it maybe is that scientists are more comfortable working with things they know are there rather than possibilities that can't be proved yet? Perhaps that's one of the main things I can bring with my background in maths and philosophy.
Absence of evidence of life on Mars is not in this case evidence of absence because we haven't looked, and we don't yet have any missions yet even on the drawing board to look at the locations where present day life may be on Mars. They can't be seen from orbit because most of the habitats are cryptic in the near vacuum Mars atmosphere - most are below a layer of dust or rock or salt or ice.
Life in such cold conditions may also be in sparse populations slowly metabolizing with individual microbe lifetimes which may even be measured in millennia (by analogy with some Antarctic populations) and have negligible effects on the atmosphere. Probably much or even all of it is not detectable even by the Trace Gas Orbiter, sensitive as it is.
And as we saw, the Curiosity 2020 sample return if it does go ahead again will not answer this question. It's not even designed to address it.
BENEFITS OF POTENTIAL NEW BIOLOGY FROM SPACE - EXTENDS FAR BEYOND THE SEARCH FOR ORIGINS OF LIFE IN OUR UNIVERSE
For those who are not especially interested in astrobiology I think it's worth saying that there are many possible discoveries and advances can come from discovery of new biology in space.
Understanding our origins better yes. Understanding how our own biology works better also by seeing how biology works with cells that work differently with different coding systems, ways of replicating, different enzymes, maybe life without any proteins such as RNA cells. Yes all of that. But it may be only the "tip of the iceberg". For instance, it may lead to multi-billion dollar industries.
I found this in an article by Charles Cockell:
"In uncovering the secrets of life's survival on the Earth, astrobiology has some found remarkably prosaic applications. The powder that works in your washing machine at high temperature functions because it contains proteins extracted from microbes that grow in volcanic hot springs."
" They were first found by scientists (who would today call themselves astrobiologists) seeking to know how life adapts to such primitive, searing surroundings."
Intriguing isn't it?
These enzymes are now used
- in the food industry, including bread making, fruit juices, for lactose free foods, for making syrups
- in the $1 billion industry of enzymes for detergents - this is another application - they work at cold temperatures so removing the need for heating and saving energy.
- for wood pulp and paper processing
- in the textile, cement, cosmetic industries.
- in various research techniques for experts studying DNA and RNA
They are used to reduce costs, make the processes more ecofriendly, reduce CO2 emissions, enable more efficient faster processing, etc etc.
They come in two main categories, enzymes from cold adapted, and from heat adapted extremophiles.
The cold adapted enzymes are more active, and active at lower temperatures. This means you need less of them to get a result, and you don't have to heat them up and they can work at low temperatures. As an example, this lets you reduce washing temperatures and to help people with limited access to warm water. The global market for detergent enzymes is valued at over $1 billion.
The heat adapted enzymes are active and efficient at high temperatures, extreme pH values, high concentrations of the substrate, and high pressures. They are also highly resistant to organic solvents, and other things that stop enzymes working (denaturing agents). They are easier to separate during purification steps (because they don't break up) and they catalyze faster reactions.
I cover this in these sections of my book Touch Mars? Europa? Enceladus? Or a tale of Missteps? :
They summarize details from this long technical paper: Cold and Hot Extremozymes: Industrial Relevance and Current Trends (paper from 2015)
If what we find on Mars is related to Earth life, but evolved on a planet with night time temperatures cold enough for dry ice, extreme desiccation, high levels of UV, and of ionizing radiation, pervasive perchlorates and hydrogen peroxide etc - we may well find extremophiles there that push the limits far beyond what Earth extremophiles can do.
Who knows what the applications would result from a new biology from Mars in the most interesting and I'd say "best case"? The case where there is a significant potential issue of contamination, yes, but also major discoveries to be made.
This could go far beyond discovery of some new enzymes. It could have applications in medicine, agriculture, nanotechnology, new materials for industry; there is simply no way of knowing what the results could be of such a revolutionary discovery as life based on different principles from Earth life, even if it is just microbes.
If we make Mars life extinct, then we are robbing not just ourselves but our children, grandchildren and all future generations from the countless benefits that may follow from the discoveries they could make by studying it.
Cassie Conley before Elon Musk's BFR announcement said:
“The excitement over this pending announcement overshadows a worrisome dilemma: The special regions where Earth life could take hold are also the areas where we would most likely find indigenous Martian life. That means—unless we are very, very careful—we could ruin our chances of discovering extraterrestrial organisms just by going to look for them."
“It’s like looking for stars when the sun's out. If you want to find Mars life, you have to get rid of the signals of Earth life so that you can see it."
NEED FOR MORE PUBLIC AWARENESS OF PLANETARY PROTECTION ISSUES
One of the things that makes a planetary protection officer's job hard is that there is so little awareness amongst the general public and even other scientists, even today, of the need for her job, and why we care about whether Earth microbes might make Mars life extinct, or confuse our studies of it. Many in the general public probably even don't know this debate is going on.
Nor politicians either. How many senators or congressmen or women know about this debate when they vote on directives for NASA? How many presidents? Was President Obama aware of this debate when he set the objective to send humans to Mars? How many know of the debate in any detail, even of those who are involved in responding to the decadal reviews which are used as feedback from the space community to help set NASA's objectives for the next decade?
Even astronomers and scientists who work in the space industry are often not aware of this debate. Particularly the many ramifications that could follow from our microbes landing on Mars.
I hope this article can help bring more public awareness of this debate. It is the first step if we are going to make a wise decision, to discuss it and think about it.
In this debate, there are many groups of people with different emphases and priorities working together.
- Hopeful Mars colonists who are vocal, organized under the umbrella of the Mars Society. They are an advocacy group and every year, they lobby Congress to support their views. They want humans on Mars as soon as possible and ask why we aren't there yet.
- Geologists who would love to have humans on the surface of Mars to study the rocks there. Their main focus is to continue to do what they know how to do, to find out more and more about the chemistry and geology of Mars.
- Astrobiologists who write papers in the academic journals about their views. But they don't have a vocal lobbying group, and for historical reasons are not much involved in decision making for space missions, not since the two Viking landers, our first and last astrobiological missions to date. Their priority is to send astrobiological instruments to Mars to search for life in situ. The only ones that get much publicity are the few ones proposing "dirty robots" as their papers are promoted by the Mars colonist enthusiasts. The responses to those papers by the planetary protection officers tend to be ignored.
- Planetary protection officers and the contributors to COSPAR workshops - and some others who specialize in planetary protection such as Margaret Race of SETI - who are tasked with upholding the Outer Space Treaty and who have spent their professional lives studying the various things that could go wrong - and urge caution.
So far the planetary protection officers have been the main representatives of those more cautious astrobiologists. But few people have heard their point of view either amongst the general public although they do a lot of public outreach work.
In their quiet way I think they are just presenting common sense myself. We should all listen to them, because they are the ones who have the most in depth and detailed understanding of what the issues are and how things could go wrong, badly wrong.
It's been their job to protect Mars and other celestial bodies, as well as the Earth (for anything returned here from space), and they have devoted their working life to this. They are backed up by many other astrobiologists who have similar views that they have published in papers and who have also looked in detail at planetary protection issues.
I hope this article helps make their task easier. I see it as my contribution towards their public outreach about planetary protection. But as someone not involved in any way with planetary protection decision making, I am free to make forthright statements about planetary protection issues, to hopefully get people thinking about this, without anyone asking me if this means a policy direction change for NASA or COSPAR :).
MORE ABOUT OPEN ENDED HUMAN EXPLORATION IN SPACE WITH PLANETARY PROTECTION AT ITS HEART
I'm not an astrobiologist, I approach this as someone trained as a mathematician who specialized in the philosophical studies of mathematical logic for several years of postgraduate study. I've had a long term interest in science generally and astronomy and space missions particularly since a child, from long before the first astronauts landed on the Moon. Patrick Moore who did a monthly Sky at Night series on BBC television in the UK was one of those who first got me enthused about space with his broadcasts. With my mathematical and scientific background, the specialist papers on this topic are easy to read and I've read many of them over the years. I am not expert in any of the topics in this field. But nobody could be expert in them all.
That helps I think, to get a wide overview of the subject, as someone who is not immersed in the field, so having a bit of a distance from it. I have no personal involvement, and no research I'm doing myself depends on planetary protection decisions. Neither am I in a hurry to get some experiment done, nor am I personally involved if we extinguish Mars life. Also I have a strong background in maths, logic, philosophy and ethics, which helps a lot with clear thinking about "fuzzy ideas" such as hypothetical biologies on Mars. I think this helps me to take a broader view on it all.
I have written three books on this topic of humans in space and ways to do both - to explore in space with humans in an exciting and ambitious way - and at the same time to do it responsibly, to protect both Earth and other planets and to leave the future open so that scientists can continue study of exobiology on Mars and in other places for as long as is needed, for the foreseeable future if it comes down to that.
My Touch Mars? book also looks at the history of planetary protection and some of the many possible locations for life in our solar system, and indeed elsewhere, and how we can search for it. Further into the future it raises the broader question of whether we need "Galaxy Protection" once we develop the capability to visit other stars, and I explore the idea of Galaxy Protection as one solution to the Fermi paradox of "where is everybody?" I also cover nitty gritty questions such as trash on the Moon, how you would grow plants in space, possible science surprises from our explorations and many other topics. I look at the practicality of human settlement and look at questions that might arise as we try to send humans further and further afield into our solar system.
I hope it's a fun read. The sections are self contained as far as possible so that you can use it as a book to dip into, rather than one you read from cover to cover.
You can read my Touch Mars? book free online here:
Touch Mars? Europa? Enceladus? Or a tale of Missteps? (equivalent to 1938 printed pages in a single web page, takes a while to load) also available on Amazon kindle. It is designed for reading on a computer with embedded videos and links, and I have no plans to attempt a printed version.
As far as I know it's the first book devoted to planetary protection since "When Biospheres Collide".
My other books, which cover human exploration as well as planetary protection, and explore the case for going to the Moon first (for humans), are:

- Case For Moon First: Gateway to Entire Solar System - Open Ended Exploration, Planetary Protection at its Heart - and on kindle - which as the name suggests explores the Case for going to the Moon first in detail, as its main focus.

- MOON FIRST Why Humans on Mars Right Now Are Bad for Science - and on kindle.
This includes my An astronaut gardener on the Moon and continues some of the themes of the Case for Moon First with a special focus on lunar gardening.
NOTIFICATIONS OF FUTURE POSTS AND COMMENTS
You can get notifications of new posts on my Science 2.0 blog by following the announcements on twitter. You can also 'like' my Facebook page: Science20 Blog Alerts
Any thoughts or comments - do say below.







Comments