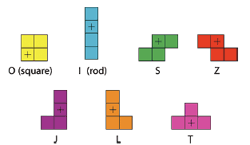
Tetris stole hundreds of hours of our lives. It’s about time it starts giving back. Researchers at the Washington University of St. Louis have built a computer simulation that uses a modified Tetris game to explore self-assembly. Their take on the classic puzzle game confirms what Tetris junkies have always known: The T-shaped tetromino is insanely versatile, and the L and Z tetrominoes just can’t get along.
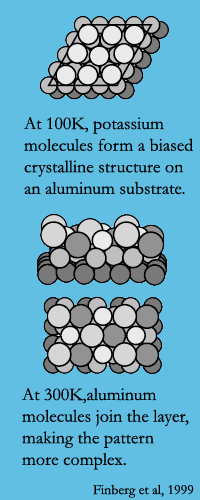Gelb’s version of Tetris mimics molecules being shot at a flat surface. One possible outcome: the molecules may form an ordered layer that minimizes the free energy of a surface. In other words, they will form a self-assembled monolayer. A monolayer composed of a single type of molecule tends to have a characteristic order to it, which is affected by both the shape and attractive or repulsive potential of the molecules. For example, at low temperatures sodium adsorbed onto an aluminum (111) surface forms a crystalline structure with a bias, as shown in the figure. When a molecule of a different size or shape is introduced to the mix, it destroys the low-energy order. Take the case of sodium molecules on an aluminum (111) surface at room temperature. They interact with the aluminum surface molecules, forming a mixed layer with a more complex pattern. Molecules try their hardest to arrange themselves in new low-energy orders that accommodate their new neighbors. To find this order, molecules have a modest ability to move, rotate, sidle themselves into holes, and bump other molecules out of the way.
In a microscopic monolayer, it’s hard to separate the attractive potential’s contribution from the shape’s contribution. Gelb’s computer model Tetris makes it easier. Differently-shaped molecules are represented by tetrominoes, and attractive tendencies aren’t built into the game.
The Tetris we know and love stacks tetrad “molecules” toward an upper limit, like a precarious pile of boxes in a closet. The gravity-style downward flow of a Tetris game doesn’t apply to the formation of a monolayer, which covers the surface like dominoes on a table. That’s why Gelb’s table-Tetris model doesn’t fill its board with pieces that meander downward from the top. Instead, the anchor point of each piece is projected to a random empty square. (The anchor point is the square with the X in it-- it acts a bit like the center of gravity.)Then each piece is assigned an allowable assembly tactic—for example, it may rotate, or translate, or even occasionally change to a different piece. If the piece can use its assembly tactic to find a situation where it doesn’t overlap existing structure, the move is accepted. The piece joins the board’s structure and the game continues.
We might expect this randomized game to return a board of well-mixed pieces, like a solution of vinegar in water. Instead, the results bear more resemblance to a pixellated vinaigrette. Rather than the 40% chance of two same pieces contacting, predicted by basic probability, The shapes pool together, forming exclusive clubs of rods, squares, Ss and Z’s. And within these clusters, the pieces tend to be uniformly aligned. This may surprise surface scientists, but it’s nothing new to hardcore Tetris players. Who among us hasn’t lost a game to a vertical tower of Z pieces?
The authors hypothesize that the pools of matching tetrominoes result from a certain symmetry of the tetrominoes. With only four units, most of the tetrominoes tend to have a front-to-back symmetry—their opposing faces line up. So by virtue of the size constraint, each tetromino forms a convenient docking point for one of its buddies. The highly-ordered stacking within each pool of tetrominoes is a telltale sign, and the T-piece is the exception that proves the rule. Unlike the other pieces, its opposing faces don’t line up well. Though it packs closely within its own ranks, the order is much more complex. The degree of shape mixing in this model tells us a bit about solubility. First, the more useless, empty white squares that are left at the end of the game, the less complementary the shape spread was. This seems elementary, but it has a real-life analog—the volume mixing fraction. If a gallon of water is mixed with a gallon of alcohol, the result will be less than two gallons because the molecules are very complementary. In Gelb's Tetris model, S and Z have a very low volume mixing fraction. S and I do not. Tetris players know that these two pieces in quick succession can be very difficult to place because the shapes aren’t very complementary. This result in the model tells us that shape can reduce molecules’ compliment as well, so volume fraction isn’t entirely an effect of attractive potential between molecules.
Second, the less shapes cluster, the more they are soluble. A combination of S and Z pieces intermixes fairly freely, with relatively small clusters. Adding L pieces to the mix causes greater cluster sizes, because the L and Z don't fit together easily.
Gelb's modified game of Tetris gives us a lot of insight into how shape can affect interactions of molecules. Even without the organizing force of attractions and repulsions, simple shapes can be trusted to find order. In the physical world, this work has implications in manmade self-assembling systems-- as "molecules" are replaced by small objects, we can't rely on attractive Van Der Waal's forces to put everything in order. The authors note that this research may also have some relevance to developing strategies to play Tetris, though they haven’t explored this angle in detail. Might I suggest a team for collaboration?
1. Barnes, B, Siderius, D, and Gelb, L. Structure, thermodynamics, and solubility in Tetromino Fluids. The results were published in the on-line edition of the journal Langmuir on April 27, 2009: http://pubs.acs.org/doi/abs/10.1021/la900196b. Not mentioned in acknowledgement section: Alexey Pajitnov.
2. S. Finberg, J. Lakin, G. Vidali, R. Diehl. Characterization of sodium and potassium adsorption on a faceted aluminum (111) surface using He-atom scattering. J. Phys.: Condens. Matter 11 (1999) 5735–5756. Disclosure: I was lucky enough to help out in this lab during my early undergrad days. At the time, I thought surface adsorption would have nothing to do with anything I'd ever work on as an engineer. Wrong, wrong, wrong.
3. US National Video Game Team: http://spyhunter007.com/us_national_video_game_team.htm I can't believe this isn't an Olympic sport yet, especially since you can knock over 1000 pins in Wii Bowling. That's better than the original.
Comments