For those part-timers who wish to move beyond the "Brief History of Time" level of physics, this is an obvious thing to try and figure out. Because gravity does not work instantaneously, there is a wee bit more wobble in the orbit of Mercury. This blog hopes to provide all the detail needed.
The book that got me over the technical hurdle was Sean Carroll's "Lecture Notes on General Relativity" from a course he taught at MIT in 1996 (chapter 7). The lecture notes are not casual reading. It took me 3-4 months to chew through them. I made my own crib sheet of the contents. Do I feel like I have an MIT graduate level understanding of general relativity? Absolutely not, I would get silence by a standard problem set. I do now have an appreciation for many more of the technical issues of the subject.
 To teach someone in my station this kind of calculation, I developed a format. Each step is numbered. The first step must always define the starting point. Nothing is left as an exercise. Each step should be described briefly - one sentence is ideal - but flexibility is allowed. The 24 steps that follow are almost exactly what is on my lunchbox I used daily. The difference is that my lunchbox references a retracted proposal of mine in the first four steps, so I modified the text accordingly.
To teach someone in my station this kind of calculation, I developed a format. Each step is numbered. The first step must always define the starting point. Nothing is left as an exercise. Each step should be described briefly - one sentence is ideal - but flexibility is allowed. The 24 steps that follow are almost exactly what is on my lunchbox I used daily. The difference is that my lunchbox references a retracted proposal of mine in the first four steps, so I modified the text accordingly.What is the big picture view before diving into the detail? The starting point is the Schwarzschild metric solution of general relativity. Physics is the art of knowing what is conserved and what can be simplified. The first seven steps set out to simplify and find the two key conserved quantities, the energy and angular momentum of the system.
The next collection of steps (8-13) are common place for people who do celestial mechanics, to switch the 1/R variable to U. Those steps still don't feel familiar. It is a rewrite that does make the resulting equation look simpler. This is past the halfway mark.
Then one solves the equation where only Newton's theory pushes the perihelion around. We need to understand that dominant solution first which is good because it is simpler. Unfortunately, it is not that simple. Planetary orbits are not circles but are ellipses. Real physicists are good enough to deal with something other than circles :-) It involves the eccentricity of the ellipse.
The solution to the Newtonian equation provides an answer to what U is. The correction term depends on U squared. Plug that back in to the differential equation. One can pluck out the one of three possible terms that is going to "row with Newton" and therefore always contribute its little bit to the precession. The on resonance term comes with its own collection of factors which are used in the final two steps to calculate the 42.9" per century contribution to the precession of the perihelion of Mercury due to the finite speed of gravity.

That is the big picture. Here now are the 24 steps.
1. Start with a solution to the general relativity field equations for a spherically symmetric, non-rotating, uncharged mass. The solution is the Schwarzschild metric written in spherical Schwarzschild coordinates.
2. Simplify by working in the plane of rotation, so
3. Multiply through by
4. Divide by
5. Define the Killing vectors for this metric.* Notice that the expression in 4 is not a function of either time t or angle phi. This means there is a conserved quantity associated with a change in time (energy E) and a change in angle (angular momentum L). Come back at a later time, and the expression stays the same. Spin around a few degrees, and the metric stays the same. The conservation law which uses a Killing vector has this form:
Here are the two Killing vectors for 4:
*The proper way to do this critical step is to write out the equations of motion, which turns out to be four equations that have an affine parameter. An analysis of the constants of the equations of motion leads to this result. Much more work is required to really get this step right.
6. Calculate the squares of the energy and angular momentum:
7. Plug 6 into 4:
What has happened? We have introduced two constant quantities, the energy E and the angular momentum L. We still have two factors of
8. Prepare for a change of variable, to
9. Plug 8 into 7:
10. Bring all the terms to one side:
11. Take the derivative of 10 with respect to phi:
12. Divide all the terms by
The first three terms are classical Newtonian gravitational physics (implied by the lack of a factor of c). The fourth is the correction required by general relativity.
13. Write out the Newtonian equation:
14. Solve the Newtonian equation. This is a slight variation on an equation with the cosine solution. We must account for the eccentricity of the circle and the constant factor. Guess a solution:
OK!
15. At the perihelion,
16. Use the Newtonian solution found in 14 as a start for the correction
term, U2:
17. Plug this into 12:
18. Keep only the second U2 correction term. The factor of
19. Guess a solution. It must be composed of the previous solution in 14, plus a way to drop the additional cosine term:
The final term in the second derivative of U will cancel with the -6 cosine term in 3U2. OK!
20. Bring the correction term into the cosine. Because
21. Calculate the ratio of the advance of phi in one rotation between the Newtonian solution, and the general relativity correction:
22. Plug the relation in 15,

23. Collect the relevant numbers:
24. Plug values in 23 into 22:
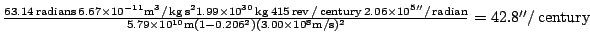
Bingo, bingo.
This number is tiny. Jupiter changes the precession an order of magnitude more than this. [Clarification: In box 40.3 of "Gravitation" by Misner, Thorne and Wheeler, they point out that the other planets Newtonian gravity also changes the precession of the perihelion of Mercury by 531" per century.] How folks did that calculation back in the days before computers is impressive.
Does Sean Carroll do the calculation this way? In chapter 7, he _derives_ the Schwarzschild solution. There is also far more discussion of Killing vectors that is well worth the read.
Doug
Snarky puzzle: The only metric that is spherically symmetric and solves the Einstein field equations is the Schwarzschild metric, or so sayith Jørg Tofte Jebsen aka Birkhoff's theorem. [Correction: The theorem applies for a spherically symmetric, non-rotating, and uncharged source for the vacuum field equations.]
Study an alternative, that will have both the right answer infinitely far away (the flat Minkowski metric), could pass weak field tests like the precession of the perihelion of Mercury, but is not a solution to the Einstein [vacuum] field equations. I like to call this the exponential metric, but it is known as the Rosen metric in the literature:
Get to step 4 of the above derivation.
Google+ hangout, Saturdays, 11am (3 people last time, a new record :-)
Next Monday/Tuesday: It's a bug, no a feature, of general relativity



Comments