I don't have a proposal right now which makes writing a research driven blog a bit awkward.  I will only say I have a proposal when I have an action, and the action has been put into the Mathematica notebook I devised in the fall of last year as part of the process that led to my retraction of GEM (the notebook tested about ten different properties of the action).


The history of physics since the 1900's has a pattern: only full time, professional physicists propose and sometimes, get confirmed a new theoretical structure.  It is a tangled team effort. Einstein leaned on Grossman to learn enough about Riemannian geometry.  It was Hilbert who wrote the action for general relativity.  Quantum mechanics had how many fathers?

Closer to our own times, the Higgs mechanism was proposed by six people.  Even if one were to drill down into one discovery, there would be many names in the local community from fellow professors to grad students that may have made small but critical contributions.  Who knows how much the Internet now adds to the discovery process?

I happen to own the URL quaternions.com, so it is easy to think I am a quaternion zealot.  I do think the amount of data visualization possible with quaternions could equal analytic geometry.  I feel the pull of multimedia analytic animations that I can download to my phone using the framework called processing. If we get the report from the LHC this summer that they are announcing the Higgs, the animations of equations is the world of research where I will go.  There is more than enough to keep me busy.

Quaternions cannot do gravity.  I know I have felt that way for quite some time.  The logic is not that difficult.  There is plenty of experimental data which says gravity can be characterized by a dynamic metric (note: there may also be other ways to describe gravity, but one way needs to be a dynamic metric).  A metric is symmetric.  Changes in a symmetric metric are symmetric.  Quaternions are asymmetric - part of a quaternion product is symmetric while the other is antisymmetric.  If I were a quaternion zealot, I would toss the antisymmetric part away and propose something made out of only the symmetric part of a quaternion product.  The universal law of attraction known as gravity seems too pure a fundamental force to do that kind of stunt.  If the results are not elegant, I am not interested.

In my second blog here, I included the graph of the always symmetric counterweight to quaternions.  I have given them a number of names, from hypercomplex numbers to California numbers, the Klein 4-group and now I am likely to refer to them as Z₂xZ₂ although some prefer the German Vierergruppe (V). The only part of that effort I hope the reader picks up is just how complicated both quaternions and these symmetric types of numbers happen to be:
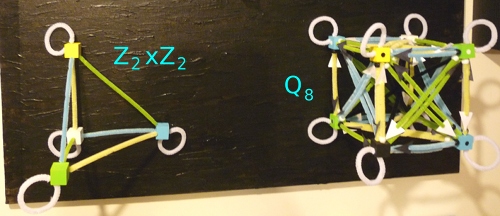
Both of these have a place for time and three separate places for values in space.  The reason these strike me as so complicated is in contrast with a continuous group that is related to the symmetry found in EM, namely complex numbers with a norm of one, or U(1).  The finite group Z₄ over the real numbers generates all of the complex numbers.  The norm of the four elements in Z₄ is one, so in the step that one does to put the "over the real numbers", if the norm is preserved, then it would represent the group U(1). [Perhaps there is already a "well known" link between the Lie algebra u(1) and Z₄ that people who know know.]

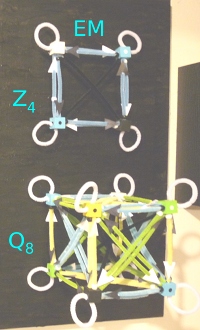I am also interested in figuring out how to describe the relationship between Z₄ and Q₈.  One could just say Z₄ is a subgroup of Q₈, end of story.  I am thinking about this in the context of physics.  As a physics operation, what does it mean to pick out a subgroup from a larger group?  This question needs to be asked in the context of doing the calculus of variations.  In that context, it looks like all the variation in space is constrained to one degree of space and one degree of time.

There is a non-trivial issue with the variation along one degree of spatial freedom.  A scientist doing an experiment is free to choose a system of coordinates.  It is a cherished principle in physics that one should be free to choose their coordinate system with no consequences other than to make a problem easier or harder to solve.  There are many times when something with spherical symmetry is described with Cartesian coordinates.

I wonder if there is an idea to find the minimal change coordinate system.  What I mean by that is the change between two objects can be described by only one spatial number that maps directly to the distance between the two objects.  As the distance between the objects change, the values from only one of the three spatial coordinates needs to be read off.  In this minimal change coordinate system, one could see the relevant symmetry of the system.

There are few finite groups simpler than Z₄.  There are few fundamental forces in Nature simpler than EM.  One could get into a bar fight over the question if gravity is simpler than EM.  As a static, classical force law, both have the same form of two charges over the distance squared.  Gravity has but one sign for the charge, while EM deals with two.  Case closed until one needs to make peace with special relativity.  That works quite elegantly with EM.  The math machinery for general relativity leap frogs the Maxwell equations in its complexity.  Gravity fields are a source of gravity.  That non-linear nature of GR makes it next to impossible to play with.

I talked with Clifford Will - an expert on experimental tests of gravity - one time before he was to give a talk at MIT.  I asked him what was the experimental support for the idea that gravity was non-linear.  He said there was no reasonable linear theory for gravity, one that could pass the current tests we know today.  That situation has not changed.

If a gravity field does not gravitate, then gravity must be simpler than EM any way one looks at it.  The gravity field theory would be required to be rank 1.  The group related to gravity would have to be both symmetric and simpler than Z₄ over the real numbers that get normed.

Here again I get to say a similar thing: how to describe the relationship between Z₂ and Z₄? One could just say Z₂ is a subgroup of Z₄, end of story.  There is an important, qualitative difference between the two graphs: Z₄ has a mix of directional and undirectional graphs, while the graph of Z₂ is only undirectional.  Sign flips happen for Z₄, but they don't for Z₂.

Doug


Snarky puzzle: Redo the Z₂ pipe cleaner graph with blue in place of black.  Comment on how that difference is trivial.  Comment on how the difference is critical.  Comment on how hard it will be to sell these two equations to the same buyer:




Next Monday/Tuesday: A Group of Snarky Puzzle Answers