White Dwarfs

Fancy a trip to Sirius?  This is what you might see as you are approaching your destination.

(Picture courtesy NASA/ESA, via the Hubble project.) 

Sirius is a multi-famous star, one of its claims to fame being the discovery of a companion.  Wilhelm Friedrich Bessel first postulated an invisible companion to Sirius A from observing a wobble in its motion, and the star itself was observed about 20 years later, while testing what was then the world’s largest refracting telescope, located in Illinois.

Actually, the ‘Pup’ (as it is affectionately known) is not the first white dwarf to have been observed.  That distinction goes to 40 Eridani B, part of a system which, for Star Trek fans, includes the planet Vulcan.  ‘Pup’ is, perhaps, rather a misleading name, because it was once the bigger star, and has burned out before its companion which is still shining brightly.

It was only in 1915, at the Mount Wilson Obervatory, that both these stars were shown to be very small, very dense, and very hot.  With the advent of quantum theory and the Pauli exclusion principle, it was understood that they are largely made of degenerate matter.  Sorry to disappoint you, but this is not something found between the ears of your least favourite politician or celebrity.

But how big is a white dwarf?  Intriguingly, the more massive they are the smaller they are, since the greater pressure inside greatly squashes the degenerate matter.  This can be seen from this famous diagram by Subrahmanyan Chandrasekhar.  It may have been already known in general before him, but in 1930, on his way by ship from India, where he had studied at Chennai (Madras) to do his graduate studies at Cambridge, England, Chandrasekhar included the effects of relativity in his calculations, he showed that a white dwarf cannot exceed 1.44 solar masses, because the pressure of the electrons in the degenerate matter cannot hold out against gravity.  This is the famous Chandrasekhar Limit. 

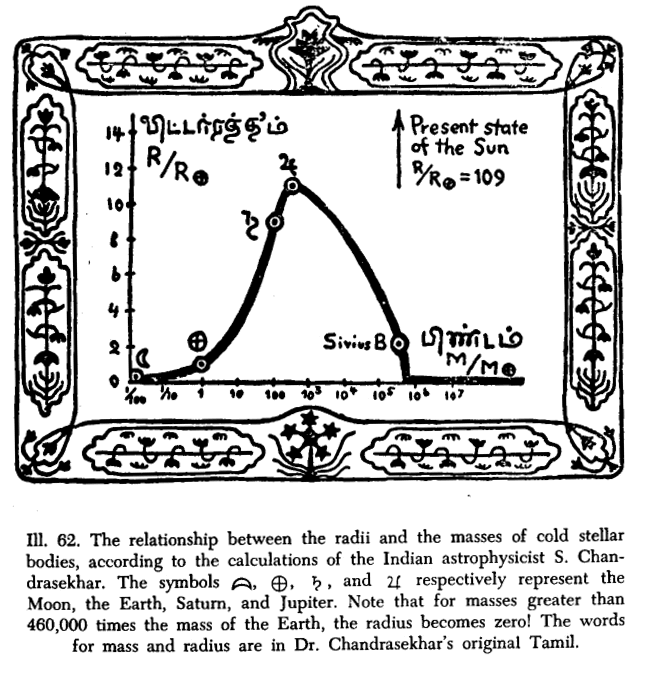(Chandrasekhar’s original diagram, from A Star Called the Sun by George Gamow.)

The situation is shown in the next diagram.  The upper curve is a calculation without relativity being taken into account, the lower curve includes relativity.  The oldest ‘typical’ white dwarf in the universe should not be much less massive than 0.4 solar masses.  Larger stars (up to about 10 solar masses) burn out to more massive white dwarfs, and there has not been time for stars less massive than 0.8 MSun to burn out to white dwarfs less massive than shown here.  Sirius B is even a little smaller than the Earth, while tiny white dwarfs very close to the Chandrasekhar Limit would be difficult to observe, and might not even occur if the pressure in the core is sufficient to force electrons and protons back together to make neutrons.  If this were to occur I would expect either a neutron star to be formed, or the whole thing to go kerblam! and disappear into the cosmos.

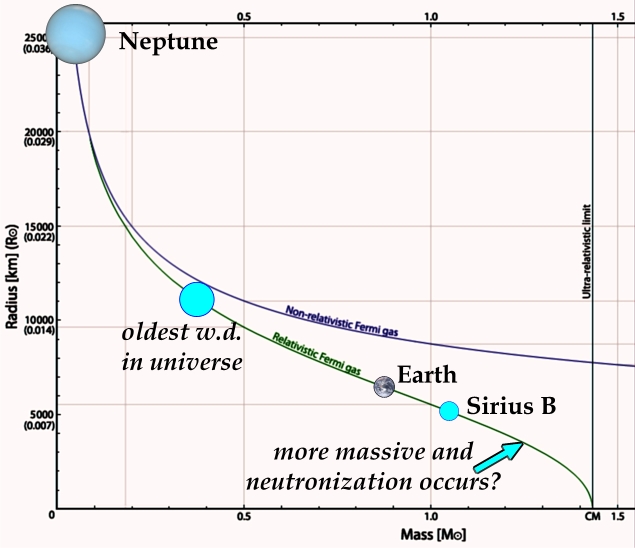
(Modified from Wikipedia "white dwarf" diagram.)

But, intriguingly, I read perhaps twenty years ago of a white dwarf of 0.2 MSun, orbiting a neutron star.  It appeared that energetic particles or radiation from the neutron star was steadily burning away matter from the white dwarf.  Indeed, this seems to be quite a common phenomenon, and very rapidly rotating neutron stars called millisecond pulsars are found on their own, which are believed to have been ‘spun up’ by a companion which they have burned away entirely.  See What is a pulsar?

This this is where I got thinking.  As the last of the material was being burned away, the remaining object would be quite big, perhaps the size of Neptune, and the pressure in the core would no longer be sufficient to force the matter into a degenerate state.  This would give an intrinsic lower limit to the mass of a white dwarf.

Neutron Stars

Neutrons are funny things.  An isolated neutron is unstable, decaying with a mean lifetime of less than 15 minutes.  There are only two known ways of keeping neutrons from decay.  One is binding them with protons via the strong force in an atomic nucleus, and this only works up to less than 200 neutrons per nucleus. Many more neutrons can be kept stable by binding them via gravity in a neutron star, formed after a supernova explosion, but that requires a lot of neutrons.  A typical neutron star may contain about 2 solar masses, the equivalent of about 10⁵⁷ neutrons.

Here again, there appears to be a practical lower limit to the size of neutron stars imposed by the mechanism of formation.  These things will only form if the core of the parent star gets close to the Chandrasekhar limit.  But by analogy with white dwarfs, I wonder if one could, by somehow blasting away material from the surface, one could reduce the mass of a neutron star, and if so, what would be its size and mass when there was no longer enough pressure to maintain its very centre in a neutronic state?

Now I don’t know of any process which could blast away material like that, but could it be that some form of baryon decay might, over a very long period indeed, bring this about?  While such an experiment would seem to be infeasible for us humans, nevertheless someone might have calculated the theoretical minimum mass for a neutron star.  And while it might require about 1.3 MSun to induce neutronization and collapse of a white dwarf, perhaps a super-compact object with the intense gravity of a neutron star could be reduced considerably below this value before it popped out into relatively normal matter again.

Neutrino Stars?

When members of our physics group were off to do neutron scattering at ISIS or ILL, Fred the Friendly Chemist would suggest teasingly “why don’t you try some neutrino scattering?”  Now while scattering a beam of neutrinos might be the only way of observing the interior of a white dwarf or a neutron star, detecting them would prove rather difficult.

But this set me wondering, might it be theoretically possible to compress a large enough mass of neutrinos into a small enough volume for it to be held together by gravity?  Neutrinos are not only very low mass objects indeed, which in itself would dictate a tremendous number of them, but they are also very fast-moving, so it would require a lot of gravity to keep them boxed in.  Maybe even, a sufficient mass of neutrinos to be held in this way would find itself inside its event horizon, and so effectively form a black hole.

But maybe not.  If so, perhaps some such objects were formed in the very dense conditions immediately following the Big Bang.  If sufficient in number, would there be enough to account for the dark matter in the universe?  They would be very difficult to detect.

Difficult to detect?  Does that mean there might be one coming our way?