FIXED, images included now...
Bell's Future Quantum Mechanics, a novel interpretation.
Start with all of space-time. All branches of physics are confined to space-time. This includes all of the physics we know today, and even the stuff we do not (what's up with parity violation for beta decay?)
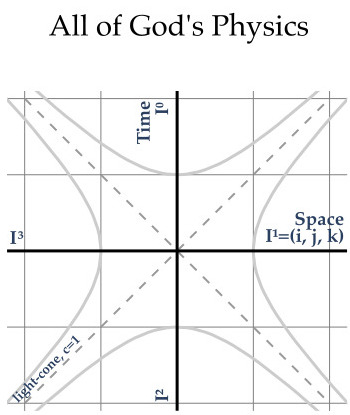
I'm explicitly rejecting more than 3 dimensions of space. I'm explicitly rejecting a multiverse.
Nature knows how to balance all of physics all the time. People are not so good at doing so much, so they break it all into smaller parts. We will do so in three acts:
1. Newtonian Classical Physics
2. Einstein Causal Relativity
3. Bell's Future Quantum Mechanics
Newtonian classical physics subtracts away nearly all of space-time.
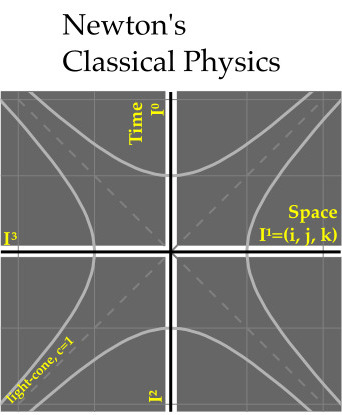
Time is absolute. Space is absolute. All of classical physics happens within the width of the time and space lines of a space-time diagram. The dark gray regions exist, but the math hardware of Newton's classical physics does not deal with it correctly, hence the blackout.
The study of EM required new types of physics. Einstein introduced relativistic physics where time can rotate into space. Einstein's math professor Minkowski created the space-time diagram. The path where light travels to and from the observer at here-now separates space-time into time-like and space-like regions.
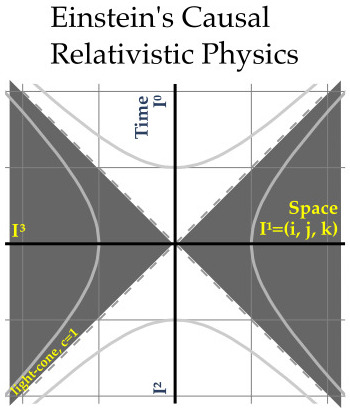
Let us focus on causality. To change the observer here-now requires an event from the past lightcone. All space-like events cannot be causally linked to here-now. Subtract away the space-like regions of space-time. The result looks like an hour glass, two cones connected at their tips.
Where does quantum mechanics go in a Minkowski space-time diagram?
At this moment in the history of physics, there is no accepted answer to that question. Newton's classical physics is confined to the axes. Causal relativity is the past lightcone, including the light-like events. Quantum mechanics must be there somewhere...
The 1935 paper by Einstein, Polodsky, and Rosen represented a challenge to the odd logic of quantum mechanics. If there were hidden local-variables, could the hidden information generate the same results? The answer is yes. It took until the 1960s when John Bell figured out an inequality that can distinguish between hidden local-variables theories and non-local quantum mechanics.
If the same question is asked the same way for an entangled quantum system, then both approaches predict the same results. When the question is asked at different angles, then that changes nothing for the hidden local-variable theories. For quantum systems, the two measurements become more correlated. Test over the entire range of angles to see if quantum mechanics is always right or if angles are consistently irrelevant.
These experiments are not trivial to do. People have criticized ways problems might sneak into the system. But the experiments from the 1980s to today have always delivered the same message: hidden local-variable theories are wrong. Quantum mechanics is nonlocal.
This creates a question: how do you enforce that quantum mechanics is nonlocal?
Try an idea: delete the past lightcone where all local variables live, at least to do quantum mechanics.
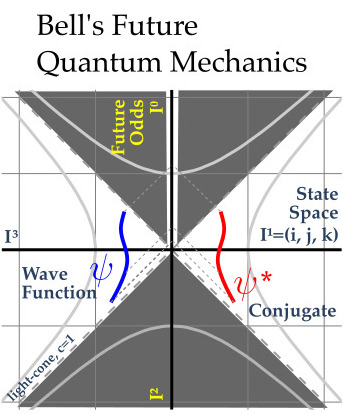
The wave function has to be space-like separated from the observer at here-now. The wave function can have nothing to do with here-now because it is too far away. Quantum mechanics has always been about the odds of an interaction happening to the observer in the future.
When I first made this image, the future lightcone was not all gray. I realized that the only information one gets has the form (p, 0, 0, 0) which blacks out most of the future lightcone.
The product of the wave function and its conjugate is the odds of and interaction happening to the observer in the future.
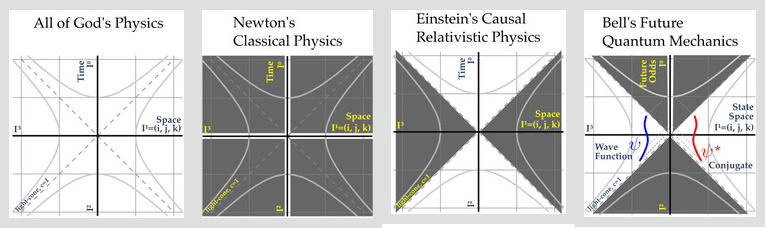
That is Bell's future quantum mechanics interpretation.





Comments