In this two-parts article I wish to describe in some detail, but still at an elementary level, the characteristics of one of the most important probes of the physics of subnuclear collisions at today's particle physics experiments: jets of hadrons originated from energetic bottom quarks, or more familiarly, b-jets. By posting a dedicated article on b-jets, I hope I will be able to describe in more detail elsewhere other physics topics, such as Higgs boson decays or top quark signatures, without being hampered by having to introduce the phenomenology and detection of b-jets from scratch every time.



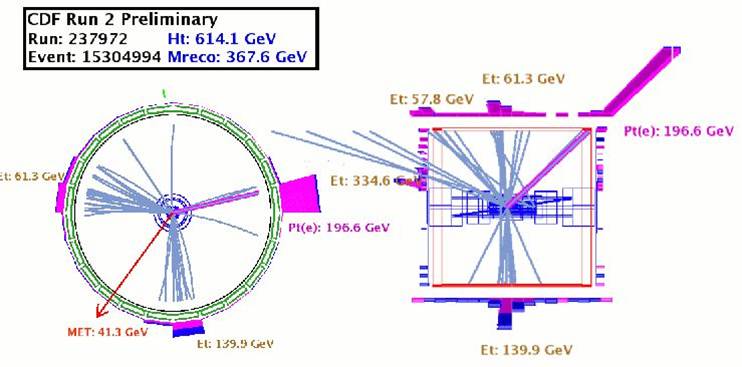
(If you wonder what a hadronic jet is, look at the picture above, showing jets detected by the CDF experiment in a transverse (left) and a cut-away view (right): a jet is a stream of particles of high energy, emitted all roughly in the same direction of the quark or gluon which originated them. By measuring the total energy and direction of the particles in a jet, we get to know the kinematics of their progenitor, gaining access to the dynamics of the production process which took place).

The reason why b-quark jets are objects of crucial importance in hadron collider physics is simple: their understanding, identification, and measurement allows us to detect the most elusive processes we can produce in high-energy collisions -top quarks, the Higgs boson, and new as-of-yet undiscovered particles that may be there, waiting to lead us into a whole new chapter in the book of subnuclear physics -the one titled "Beyond the Standard Model".


Why are b-quarks special ?


Bottom quarks are by themselves exceedingly interesting objects, but we know them inside out by now, thirty-two years after their discovery. Leon Lederman and his collaborators found proof of their existence in the quarkonium resonances, the Upsilon particles, in 1977 (see the figure on the right, showing the apparatus, and the figure below, showing the peak due to Upsilon production in the distribution of masses of muon pairs). Since 1977 we have amassed more information on b-quark properties than on any other Standard Model (SM) particle, except maybe the Z boson. Not a surprise, if you consider that two of the most successful present-day particle physics experiments, BaBar in California and Belle in Japan, have been designed, built, and operated specifically to study hadrons containing the bottom quark.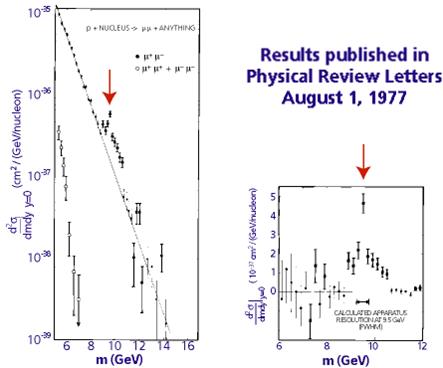



The bottom quark belongs to the third generation of matter (the third column in the picture on the right), the one which includes its partner, the top quark, as well as the tau lepton and the tau neutrino. There are several theoretical reasons to expect that a deep investigation on the phenomenology of these bodies, which are more massive than ones belonging to the first and second generation, can shed light on what lies beyond.

For instance, in supersymmetric theories the "superpartners" of these standard model (SM) particles are often the lightest ones, and thus the simplest to detect, when their decay involves their top and bottom SM partners.

Another reason to study third-generation fermions is that the Higgs boson "couples" to SM fermions in a measure proportional to the square of their mass, and thus top and bottom quarks are favored with respect to lighter ones when the study of the Higgs is in order. Due to the intense coupling to the Higgs, it is through top quark pairs that hadron collisions most often produce the Higgs particle; similarly, bottom quarks are also the fermions into which the Higgs most likely decays, if top pairs are disallowed by the insufficient Higgs mass.

An intense coupling to b-quarks is also a characteristic of Supesymmetric Higgs bosons. In much of the still-unexcluded parameter space of SUSY theories, the coupling of the lightest Higgs boson (there are five of them) is strongest to down-type fermions, such that a very important signature of Higgs production and decay is the appearance of events with four b-quark jets: two from the Higgs decay, plus the two which radiated the Higgs in the first place.

All the above points explain why we may expect that events containing b-jets may be interesting to study. However, this information would be useless if b-jets were produced just as frequently in less interesting processes. So the most important reason why b-jets are valuable lies in the inner workings of Quantum ChromoDynamics (QCD), the theory of strong interactions. In hadronic collisions, QCD is virtually the only game in town: when protons collide they almost always do it by interacting strongly, yielding hadronic jets. Luckily, in generic QCD interactions only a percent or less of the time b-jets are produced: almost always, the jets are due to the hadronization of lighter quarks, or gluons. So the presence of b-jets in an event is rare, and it constitutes an important indicium, like finding Amanita Muscaria when you are looking for Boleti (left). Never gone in search for mushrooms ? Too bad for you, but you probably got the idea.

Part of the reason for their rarity in QCD interactions is the fact that b-quarks are not legitimate inhabitants of the colliding hadrons (be them protons or antiprotons): they exist inside light hadrons only for vanishingly small instants of time, and it is thus a very rare occurrence that a proton-proton collision involves one of them, much like taking a random picture of the sky as in the banner above and finding a meteor streak in it.

The other reason for expecting few b-quarks in a QCD interaction is the fact that they are massive, and so the reactions which produce them are not quite frequent. QCD never creates "flavour" (any specific brand of quark) out of nothing, so the only way to produce a b-quark is to create it in pair with its anti-particle (bottomness cancels out with anti-bottomness, and QCD is ok with it). All in all, a gluon must be ready to spend more than 8.4 GeV into the mass of the two quarks, in order to produce them.  


More special features


Besides the peculiarities of its production in hadron collisions, the bottom quark has several characteristic features that make it unique. Its mass, which is of about 4.2 GeV, is so much larger than that of lighter quarks, that one can easily describe the hadron it creates when it combines with an up, or down, or even a strange quark as a planetary system, with the bottom quark sitting at the center and the lighter quark jiggling around. There is a whole theory describing in this way the behavior of these intriguing hadrons, which is called Heavy Quark Effective Theory (HQET in short): HQET describes the properties of bottom hadrons quite well by using this planetary approximation as a starting point.

A second crucial property of bottom quarks is that they are long-lived: the hadrons containing them take forever -on a subatomic time scale- to disintegrate, by means of the weak interaction: the lifetime of B hadrons is of the order of one picosecond, i.e. a millionth of a millionth of a second. Now, a trillionth of a second may look like a bit too short a time interval to be dubbed "forever", but if you compare it to the lifetime of particles decayed by the action of the strong interactions -bodies which live a trillion times less yet!- you understand the reason for the optimistic adjective.

In a trillionth of a second a particle moving at a speed close to the speed of light can travel a few millimeters. Since here lays one of the most important consequences of the peculiarities of bottom quarks from an experimental standpoint, it is maybe worthwhile to explore the statement further. This will lead us to digress into the top discovery, but it will be a fruitful digression.


B-jets contain discernible secondary vertices


Let us take a meson: it is a particle composed of a bottom quark and a anti-up quark. The two quarks are bound together inside the meson by gluons, the carriers of strong interactions. The  meson only decays when the b-quark inside it manages to transmute into a lighter charm quark, releasing the remaining energy in the form of a virtual W boson (the carrier of the weak interaction) which immediately materializes into a couple of other elementary particles. Now, let us assume that this particular meson lives for exactly one trillionth of a second: how far away does it travel from the point where it has been produced, before decaying ?

Of course, it depends on its speed : speed, even in relativistic mechanics, is to be multiplied by time to get a distance . However, while if the  were a bullet we would simply do , in relativistic mechanics we must add a factor to the formula, one which accounts for the dilatation of times in the reference frame where we observe the particle. I do not want this article to become a lesson on relativity, so I hope you will acknowledge the fact, and let me just state that we have to multiply  by a factor called "gamma", which equals one only if the speed is very small, while it grows indefinitely as approaches the speed of light.

To cut the story short, we need to know the energy with which our meson has been kicked out of the collision point, if we want to compute how far it travels in a picosecond (a trillionth of a second, as you have already made out). So let us assume the meson has a total energy of 52 GeV -a value which is a quite good reference point when discussing the decay of Higgs bosons or top quarks, as we will see later. If the energy is 52 GeV, we find gamma by dividing it by the mass, which is 5.2 GeV. We get : such a large relativistic factor implies that the meson speed is basically equal to the light speed . So at we end we have .

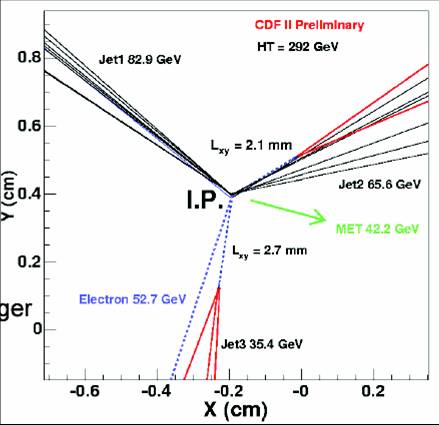
Three millimeters, an eight of an inch. Not a ballistic distance, but definitely a macroscopic one -I can witness that, since I still remember punching with a hand drill about 200 quarter-of-inch holes in eight-of-an-inch sheets of stainless steel, during one of the least inspiring days of my post-doc years (see me on the right, leaning on said sheet of steel, cover of a CMX muon detector wedge). Here we get to know why the b-quark lifetime is an important attribute from an experimental standpoint: we can measure the travel distance of b-quarks if we precisely determine their creation point and their decay point. By finding the travel distance not only can we then measure the B lifetime -which in turn allows to constrain a few of the free parameters of the Standard Model; we also have a means of recognizing B hadrons from all other particles produced in hadronic collisions, which have lifetimes so much smaller they never make it away from the collision point. This feature allows us to "tag" the b-quark, a fact of crucial importance.


B-tags and the top discovery


The decay of a B hadron often produces several charged particles, each endowed with enough energy to produce recognizable trajectories in a precision tracking device. These tracks can be traced back to a common intersection point: a secondary vertex. The CDF experimenters understood at the end of the eighties that secondary vertices from B hadron decay needed to be reconstructed in order to increase the chances of a top quark discovery. They installed a brand new silicon microvertex detector in the core of the experiment in 1992, just before the start of Run I.

A multi-layered cylindric detector surrounding the beam axis was built with 300-micrometer-thick wafers of silicon, shaped in thin strips spaced 55 micrometers (the "strip pitch", see technical drawing on the left). The passage of charged particles through the 300 micrometers of semi-conductive material released about 20,000 electron-hole pairs; a mild electic field brought these to drift toward a few adjoining strips, where the spatial centroid of collected charge provided a 10-micrometer resolution on the position where the charged particle had crossed the layer. Through the lining-up of three or four such centroids on the concentric layers of silicon, CDF could reconstruct track trajectories well enough to "see" that these particles came from a secondary vertex, and thus tag b-hadron decays. The figure below shows tracks coming out of a proton-antiproton collision seen by CDF: this is most likely a top pair production event. Two of the jets contain secondary vertices, identified with the tracks displayed in red. These two secondary vertices are crucial identification handles to select the top event in the figure.



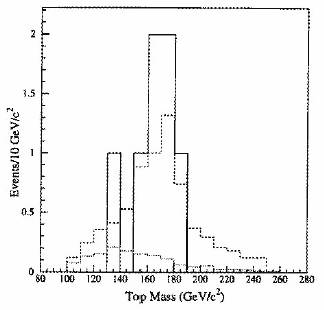Facts proved that CDF was right: the first seven, clear top-quark candidates obtained by CDF in 1994 over a very small background (small because few background events had identified b-jets!) allowed it to publish the first evidence of top-quark pair production before DZERO could touch ball, and measure the top mass at a value amazingly close to today's world average, 174 GeV. The figure on the right is the mass distribution in question, published in the 1994 "evidence" paper (the full histogram shows the reconstructed top mass in the seven events, the dotted and dash-dotted histograms show the expected background distribution and the top plus background expectation). There is ground to be proud of being a  CDF member!  

After 1994, the last 15 years at the Tevatron have seen an explosion of studies on how to trigger, detect, reconstruct, and measure b-jets. Nowadays the vertex reconstruction efficiency of an energetic b-jet is 50% higher than it was in 1992, and secondary vertex tagging has become a reliable, optimized tool to select top-quark decays and to search for Higgs bosons. Since CDF paved the way, no hadron-collider experiment has or will ever be conceived without a silicon inner detector any more. The technology to build, operate, and read out these devices has become so refined that the CMS detector at the Large Hadron Collider has been equipped with a hundred square meters of such high-precision detectors! Check the CMS tracker out in the figures above on the left and below: besides being an absolute technological marvel, it is mindboggling to know its inner workings. But getting to know that detector alone would require a dedicated post, or rather a series. Instead, we must stop here for today, and take stock.



Summary for part I

In this post I have tried to provide some of the reasons why b-quark jets are such an important object to study in detail at hadron colliders, and I gave a short description of the most powerful way by means of which b-jets -which are otherwise quite rare- are identified in hadron collisions. This led us into a short digression on the top quark discovery.

In the next part of this article I will discuss another method to identify b-jets, soft-lepton tagging, and the reason why this method works. This will take us into a digression on the phenomenology of weak interactions. Then we will discuss the energy measurement of b-jets, and its crucial importance in the investigation of particle physics at the high-energy frontier.

Needless to say, I will be quite happy to receive feedback on whether the level of this piece is adequate to your understanding of the matter, as well as to answer any question you have on the topic discussed above.