I think I owe to all of you, who came here to read this post, an explanation - if a quick and dirty one - of what Altarelli's equations are and what is their purpose. (Yes, Altarelli's equations tonight - not DGLAP for this once). So let me try and explain them to ANYBODY who is willing to try and understand.
Particle physics experiments in the sixties and early seventies of last century probed the structure of the proton, which was little by little understood as a very complex object made of smaller bits called quarks and gluons. Both these particles carry a particular kind of charge that they can exchange by interacting. Quarks in fact "feel" the presence of other quarks by exchanging gluons among them, much like electrically charged bodies interact by exchanging photons.
The electromagnetic force works by photons being exchanged, and the strong force between "partons" -as collectively quarks and gluons can be called- works by gluon exchange. The gluons, therefore, are not just the messengers of the force, but they act as sources of the force field themselves. This small difference makes the strong force extremely different from electromagnetism!
What the study of energetic collisions of electrons, muons and neutrinos with protons had revealed in the sixties was a property called "Bjorken scaling": it looked as if it did not matter how energetic was the collision if you counted the probability of its occurrence; that probability only dependend on dimensionless kinematic features of the collision. That was something that would only happen if indeed the proton was made of small pointlike bodies (quarks were convincingly shown to be the actual constituents of the proton and other hadronic particles only in 1974).
But Bjorken scaling was only an approximate rule. Altarelli and Parisi showed that a theory of interacting quarks and gluons predicted that this scaling would break up in the general case, as the probability to find a quark with a given energy inside a proton would depend on its chance of being originated by a higher-energy quark which emitted some of its energy in the form of a gluon. The Altarelli-Parisi equations formulated in a quantitative way how this scaling violations could occur, by predicting the "evolution" of the energy fraction carried by quarks as they interacted by gluon exchange.
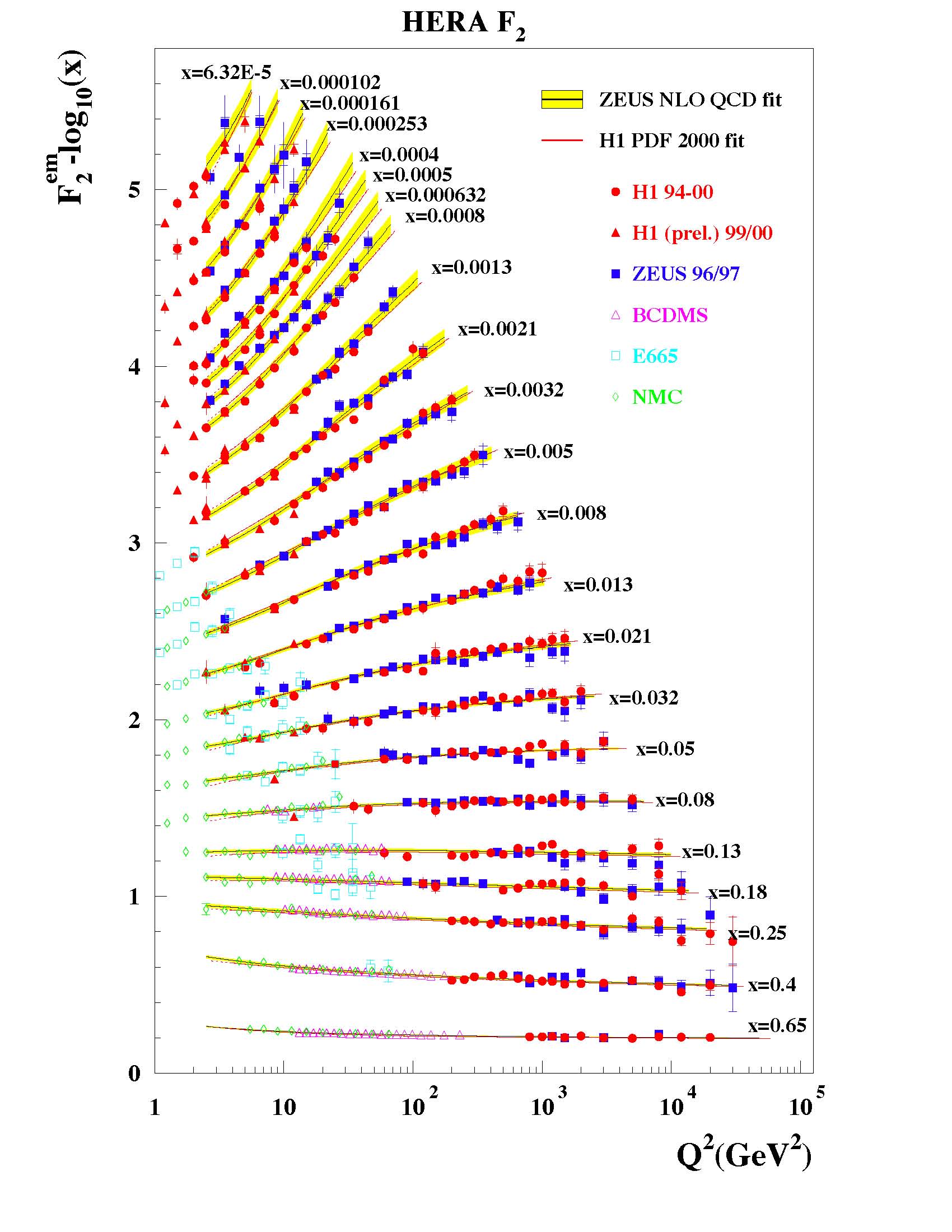The picture on the right shows today's knowledge of "parton distribution functions", which are probability distributions measuring how likely it is that a quark or gluon is found within a proton as a function of the energy it carries and the energy of the collision that probes the proton's interior. I won't explain the detail - just admire the graph for the enormous amount of information it enshrines. It is all understood thanks to Altarelli and colleagues.I realize I must stop here, as the text above is both as inaccurate as I can bear myself to write, and as complex as a non-physicist can grasp (or worse, unfortunately). But you may understand the general point: the equations explained the behaviour of a complex system made of quarks and gluons, what we today know is the proton, and allowed to predict a number of characteristics that could be measured with high precision in the forthcoming decades.
So farewell, dear Guido. I first studied your work in textbooks, and then had the privilege to meet you - in Boston, at CERN, in Split, in Rome, and in a number of other occasions. I never remember you angry or in a bad mood - I rather remember your broad smile.
Comments