Why should we bother building mathematical models of biological systems? Scientists from other fields might wonder why one would as such a question - physicists, climate scientists, economists, engineers, and chemists all use mathematical models to understand the world.
Some biologists do too - individual proteins are studied with quantum mechanical models by biophysicists, enzyme reactions are modeled by biochemists, physiologists have mathematical models of the circulatory system, and population geneticists model the evolution of gene frequencies in populations.
However, there is a big gap between biophysicists and physiologists - in the realm of molecular, cell, and developmental biology, the value of building mathematical models is not widely accepted. For good reason too - for close to three generations now, molecular biologists have made fantastic progress without turning to math. Verbal or cartoon models of molecular systems have been sufficient for working out the fundamentals of cell division, embryonic development, cell signaling, etc.
To be fair, over the decades, some researchers have used mathematical models to study molecular cell biology, and some of these models were clearly successful. However, almost none of this work is widely known: you don't find it in textbooks, classes, most conferences (even ones devoted to systems biology), and journals. Mathematical modeling has not changed how the vast majority of molecular biologists do business - in contrast with genomics, which has infiltrated just about everything we do.
Dynamical Properties are Interesting
So most biologists need some convincing that mathematical models are useful. Why bother with models?
Molecular biologists should care about mathematical models because it is only through such models that we can study dynamical properties, and dynamical properties are interesting and important. They, as we'll get to below, 1. are biologically relevant, and 2. enable us to make sense of complex phenomena in terms of a few underlying principles.
What is a dynamical property? For an illustration, I quote Foster Morrison, author of The Art of Modeling Dynamic Systems:
Most American dictionaries do not distinguish between dynamic and dynamical. There is good reason to do so, however. Dynamic means changing. Dynamical is what concerns change. The position of an artificial satellite changes rather rapidly by earthbound standards, so it is very dynamic. The orbital energy of the satellite changes very little - not at all to a certain level of approximation - so the orbital energy is a dynamical property.
Analyzing complicated systems need not require great mathematical sophistication or intellectual brilliance. But it does require clear thinking, the kind of thinking that distinguishes sharply between the dynamics of change and the unchanging dynamical principles needed to analyze change.
This is a great illustration from physics - what about biology? Calculating the orbital energy of a satellite (to a first approximation) is a homework problem in Freshman physics. Are there genuine biological examples?
Bistability
Molecular biology is really full of examples of dynamical phenomena, right underneath our noses, perhaps dressed up in language that most molecular biologists aren't that familiar with. One of the most interesting dynamical properties of genetic regulatory systems, the one which I'll focus on here, is bistability. Bistability is absolutely critical for some of the most basic cellular processes. How bistability is produced and maintained under a wide range of environmental conditions is something that can only be answered mathematically.
What is bistability? A bistable system is one that can exist in two discrete, stable states, without the existence of any intermediate stable states. Think of a light switch - one without a dimmer. You're either off or on, not part way on. And once you're in one state, you don't just drift back into another: a wobbly light switch that won't stay in the 'on' position is not very useful.
We don't want wobbly switches in the cell either. A cell frequently needs to switch to another state, irreversibly, and without transitioning through some graded intermediate. For example, microbes transition among various metabolic states. A yeast cell, in the presence of the sugar galactose, needs to be in a galactose-metabolizing state, not a glucose-metabolizing one. A cell undergoing the process of division, needs to enter a discrete 'DNA replication' state, and not slide into a state where it's trying to partition its (unreplicated) chromosomes among daughter cells.
(An elaboration on what I mean by cell state: basically, it means that certain genes are 'on', and certain signal relay pathways are firing, while other genes and signaling pathways are off. The end result is that the cell performs one specific function, and not some other, mutually exclusive function - it's producing proteins to import and metabolize galactose efficiently, not glucose; or the cell is replicating its DNA, and not partitioning chromosomes. We can also talk about the state of individual genes - either on or off; state transitions of individual genes are great examples of bistability.)
Creating Bistability through Positive Feedback Loops
This brings me to a recent paper published in PNAS (hat tip here to my CGS colleague Yue): Building biological memory by linking positive feedback loops, by a group researchers at the University of Michigan.
Researchers, when talking about bistability in the cell, often invoke "biological memory." What they mean here is that the cell switch 'remembers' that it has been flipped by a chemical signal - remove the signal, and the switch still remains in its new state. Cellular memory sounds cool, but it's not much different than your light switch 'remembering' that it has been flipped on. So don't get lost in the jargon.
This neat paper is about building a bistable genetic switch. The question the authors ask here is not, how do you get bistability, but rather, how do you make bistability a robust property of a system under a wide range of conditions?
They briefly summarize how you get bistability in the first place:
Theoretical studies have argued that the minimal requirements for genetic bistability are twofold. First, there must be some type of positive feedback controlling gene expression. Examples of positive feedback are when an activator protein drives its own expression or when an even number of linked negative regulatory steps are present, such as when a repressor blocks the expression of a repressor of its own expression. Second, the kinetic order or sensitivity of the system to the positive feedback element must be high (8, 10–12). For example, in the simple case where a transcriptional activator drives its own expression, the response of the transcriptional promoter to the concentration of activator protein must display a kinetic order or sensitivity greater than one (8, 10–12). If these minimal requirements are met, bistability may be anticipated to occur under some environmental conditions.
The researchers pick it up from here: they note that in nature, bistable systems generally aren't made with just single positive feedback loops. In other words, real systems don't just meet the minimal requirements for bistability, probably because these minimal requirements don't produce robust bistable switches.
So the scientists built a synthetic genetic system in E. coli, using two positive feedback loops. I've drawn a simplified version of their Figure 1 below, so you can see how the system is wired up. The goal is to control the gene lacY in a bistable manner - it's either on (being transcribed) or off. Whether it's on or off depends immediately on glnG, which is a transcriptional activator, promoting the expression of lacY.
There are two positive feedback loops here that ensure that once lacY is on, it stays on. First, glnG activates its own expression - once glnG is on, it keeps itself on, and thus keeps lacY on. Second, lacY promotes the uptake of the chemical IPTG, which inhibits the repressor of glnG, lacI.
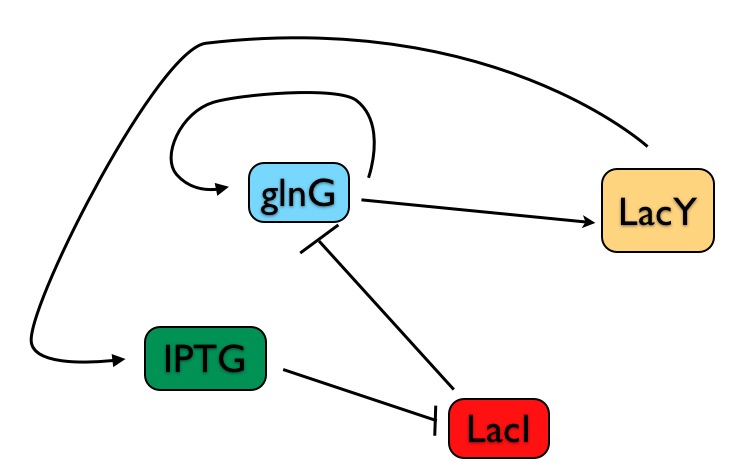
The system begins in the off state - when no IPTG is present, lacI keeps glnG off, and the whole system is off. If you add enough IPTG, lacI is rendered ineffective, glnG revs up, and then starts making both more glnG and lacY. As the two positive feedback loops kick in, you can begin to withdraw the IPTG, and the system stays on.
Perturbing the System
As I mentioned, the real purpose of this research is not to simply create a bistable switch. It's to explore what makes this switch robust to a wide range of environmental conditions. In this case, the primary environmental condition is the concentration of the chemical IPTG. What the researchers were looking for was a system with the least-wobbly switch: one that requires a big signal (lots of IPTG) to flip on, but one that then stays on when the signal was removed.
To explore this, in addition to the double positive feedback system I drew above, the scientists tested systems with only one of the feedback arms - either glnG activating itself or lacY promoting the uptake of IPTG. Their results were dramatic: the double feedback system was a more robust bistable switch than the single feedback systems: it stayed off until treated with a very high dose of IPTG, and then, once flipped on, it stayed on even when the IPTG was completely removed. In other words, each of the two states was more stable in the double feedback system, and a large signal was required to flip the switch.
The researchers can explain this phenomenon with their mathematical model. I won't get into the details here, but in essence, they engineered an interesting biological switch and they have a rigorous theoretical understanding of how that switch operates. In this particular paper, they studied a synthetic, but the wiring diagram strongly resembles many switches found naturally.
Double feedback is everywhere in biology. There are very few simple regulatory systems in the cell. These feedback loops are largely incomprehensible without mathematical analysis. The dynamical properties of these regulatory systems are key to their function, and without models, we're blind to these properties.
UPDATE: I glossed over the details of the model because of this piece is already long, but stay tuned for a future post on the math behind this.
Read the feed:






Comments