The article Neutrinos CAN go Faster than Light has triggered large interest and is at present widely discussed, for example here and here on my favorite (for variety and reliability) German science column Here There Be Dragons and somewhat here at Ethan’s always exciting startswithabang. The discussions however revolve around hypothetical extra dimensions, but extra dimensions are unnecessary:
Superluminal velocities do generally not violate relativity, or help you to time-travel, or violate causality as long as there is only a single reference frame relative to which the propagation happens instantaneously. Yes, you read this correctly: even infinite velocity can be accommodated in Einstein’s relativity, and the necessary reference system could perhaps be as simple as a quantum tunnel barrier – no need to invoke exotic cosmology.
The pedagogic extra dimension example was mentioned because it is so very intuitive; lay people can plainly ‘see’ how faster than light propagation does not kill Einstein’s relativity. Let us investigate this today without extra dimensions. Just to remark quickly on the current relevance of all this: If, as was reported [1], neutrinos actually went faster than light from CERN to OPERA in Italy’s Gran Sasso, which I hold unlikely (yet not entirely unexpected for neutrinos), they can do so by involving short-distance phenomena many times faster than the speed of light without violating relativity or causality not only in case something jumps into extra dimensions but also if everything stays inside our usual three dimensional space.
I will start with the circumstances under which superluminal signaling does violate causality. Scroll through to the next section, section 2, if you are only interested in how this is resolved.
1) How Faster than Light goes back in time to kill Bob’s chances of dating Alice
Faster than light particles are called tachyons, and as you can find on the Wiki page on tachyons:
As noted by Gregory Benford, among others, special relativity implies that tachyons, if they existed, could be used to communicate backwards in time (see Tachyonic antitelephone article).
The problem is the following: Alice is a really hot girl and has a crush on Bob, but of course only as long as Bob does not call her first. If Bob calls first, he will appear too eager for a date and totally lame in Alice’s mind. Now it is already 12 o’clock on Saturday and Bob is a popular hunk, so Alice better waits no longer; she sends an infinitely fast tachyon to Bob, meaning relative to Alice, the tachyon starts (event P) and arrives (event Q) both at twelve o’clock, that is t = 12h.
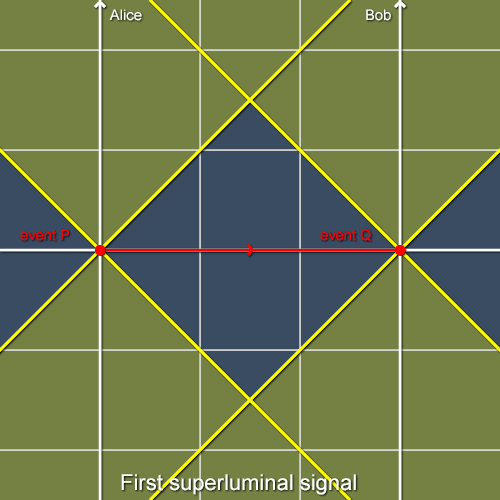
Alice sends a tachyon to Bob. Here, Bob does not move yet relative to Alice, which we will though soon assume.
The tachyon arrives at t* = 12h also relative to Bob’s clock showing time coordinate t*. Now consider that when Bob receives the tachyon, he happens to move away from Alice, speeding on the super freeway with half the speed of light or so. This implies that the tachyon started (event P) at time t*> 12h, perhaps at one o’clock relative to Bob’s current reference system: t* = 13h. There is nothing wrong or problematic with this yet, because time labels are first of all just that, labels, and you can easily understand why all this is true even without any formulas. This has been explained well enough merely employing pictures here, which is where I stole the above image.
Now where is the problem? The problem starts if on reception of the tachyon, Bob is allowed to perform the same procedure that Alice did, namely, he may immediately hit the answer button by accident and send the tachyon right back to Alice in the same manner as Alice did: The tachyon is starting (event Q) at t* = 12h and arriving (event R) instantaneously at the same time t*= 12h, too, but this time relative to Bob’s time t* because he is sending it. The situation is symmetric to that described before; Alice moves away from Bob because Bob moves away from Alice. No different from before, such implies that according to the receiver’s time coordinates, the sending happened one hour later. If the sending (event Q at t = 12h) happened one hour later, it must be now one hour earlier when receiving it (event R at t = 11h).
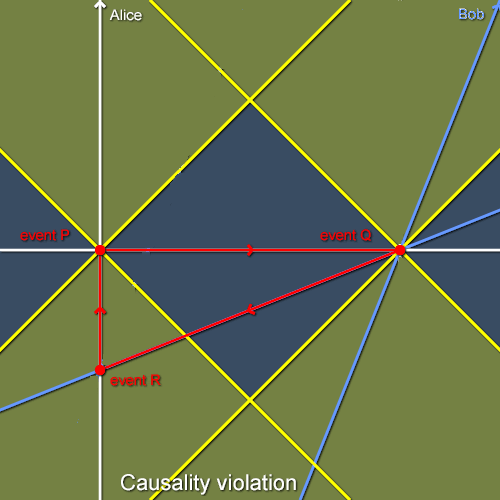
Picture stolen and then marginally altered - hope nobody sues me for this.
Alice started the whole business at t = 12h but she receives the answer from Bob before that at t = 11h. This cannot possibly be, because Alice is very attractive and would not send any message to Bob at all if he contacted her first and moreover at 11 o’clock on a hung over Saturday morning. Causality is violated.
Some conclude relativity is wrong; most conclude that superluminal velocities are impossible; both conclusions are mistaken.
2) Why Faster than Light does not mess up the Date
However, all hangs on one assumption: “The problem starts if on reception of the tachyon, Bob is allowed to perform the same procedure that Alice did, …”. “Same procedure” means here sending something instantaneously relative to ones own reference frame. If Bob can do the same, causality is violated. However, assume for example that Alice can only do so because she happens to be almost at rest relative to the cosmic microwave background (CMB), which is a rather special reference system left over from the big bang. In other words, the tachyon is instantaneous relative to the CMB. Bob moves away from Alice and thus relative to the CMB, therefore he can not send it back to Alice instantaneously relative to his own reference system.
One may equally consider that the instantaneous communication is bound to the membrane universe discussed last time, or say relative to the CERN muon reaction tunnel or even some telecommunication company’s private quantum communication tunnel device* which moves at any desired speed relative to the CMB (yet no possibility to have two such tunnels moving very fast close to one another without destroying each other). In all these cases, Bob sending the tachyon back will send it straight back from event Q to event P; it does not go back into the past.
(* Off the red thread Remark: According to many physicists, instantaneous quantum correlations may occur in the Einstein Podolsky Rosen problem. There, the one necessary unique reference system relative to which instantaneous ‘interaction’ may occur is – with much poetic license – the split where the many worlds interpretation’s multiverse branches. Be aware however that the recent resolution of the EPR paradox needs no faster than light correlations. In fact, I do not hold it likely that any of the measurements that hint at instantaneous quantum tunneling will hold up to scrutiny, but this is my personal opinion.)
There are two ways to understand all of the above better:
2.1) One way is to look at the so called light cone structure. The following illustration depicts a somewhat similar situation (not quite the one described above), namely one where there is also an event, here event E, that according to Alice is in the future but according to Bob is in the past. As you can see, while this would be completely impossible in Newtonian physics depicted to the left, in relativistic physics, not all past is already determined past (stuff that actually happened and is done with, decided, finished).
(a) Galilean relativistic Newton space-time, i.e. space, namely the x-direction, living through absolute time t = t*: The t-axis is Alice’s world line while the t*-axis represents the history of Bob. (b) Einstein relativistic Minkowski space-time: Bob moves with about a third of the velocity of light c/3 to the right. The event E occurs at t > t0 (Future) but at t* < t0 (Past) although both observers meet at t0 and synchronize their clocks then. (Illustration from reference [4], all rights reserved)
The determined past is inside the dark gray cone. Even if signals go forth and back with infinite speed along any of the x-axes, they cannot ever reach back into the determined past and change it (as long as they do it along the same x-axis and do not hop around between different reference frames).
2.2) The other way is perhaps the simplest, namely to imagine the universe to be like the surface of a pond of water. The following is adapted from the section “4.1. Causality preserving superluminal velocity but no time-travel” of reference [2]. It is a little long, so let me first point out two important points to keep in mind:
1) It mentions splashing water which invokes extra dimensions orthogonal to the universe that exists inside the pond's surface. This is only didactic and for example shock waves and sound can also travel through fluid much faster than the surface waves can do.
2) The main point is that the physics observable, the mathematical structure valid inside the fluid’s surface, is that of Einstein’s relativity. The conclusions (e.g. no time travel) hold regardless of whether or not the universe actually has such a fluid. All that is necessary is that superluminal signals travel at most instantaneously relative to a certain reference frame; obviously that does not need to be a pond of fluid. The fluid is a didactic tool just like the extra dimension, because when thinking about a fluid, no equations are needed to prove certain facts: We all take baths from time to time and thus we all know perfectly well that no wave or splashed drop can visit the water’s past, can somehow revisit wave patterns that simply do not exist anymore.
Considering a pond of fluid, splashed drops may reenter the surface after traveling above it with higher than the low energy wave speed c observed by observers living inside the surface:
Observers are made out of the waves on the pond and must choose as their “light” the fastest to them available excitations with few internal properties. Having no better measure, light must be used to measure light, thus it always has the same speed c. All objects are made out of simple waves trapping each other in patterns (pseudo particles). A pattern moving relative to the liquid’s molecules experiences time dilatation: A light-clock is a simple light wave bouncing between mirrors. If the clock moves with close to the speed of light, bouncing light needs much pond-time to reach the receding front mirror. The universe of these observers is special relativistic. A Minkowski space-time diagram suffices to establish that systems at rest in the pond also undergo time dilatation as measured from moving patterns (relativity)! The observers cannot measure how they are moving relative to the pond.
A mathematical model based on this picture is at low energies special relativistic inside the surface, yet allows faster than light phenomena that do not violate causality. The splashed substance carries at least the information that a high energy experiment has taken place. Superluminal information carrying phenomena need not violate causality if the signal travels at most instantaneous relative to the cosmological space-substance, i.e. it is tied to one and only one reference frame!
Since special relativity is valid inside the surface, there are inertial systems relative to which the superluminal splashing goes backwards in time, but in none does it splash into their past light-cone (which is their causal past). No equations are needed to prove it: We all take baths and know that no wave or splashed drop visits the water’s past. Imagine you stand next to a pond watching some sentient beings made from the pond’s surface waves: the futility of their efforts to invent a time-machine is ridiculously apparent. A space-substance giving rise to general relativity in as far as it is confirmed by observations renders the idea of time-travel equally ridiculous: Excitations of a substance cannot visit a previous state of the substance that plainly does not exist anymore. Deriving such results as far as they apply to special relativity from an abstract viewpoint that refuses to consider fluid ponds needs many pages, equations and diagrams [3]. It is basically impossible to do so didactically for general relativity.
----------------------------------------------
[1] OPERA Collaboration: “Measurement of the neutrino velocity with the OPERA detector in the CNGS beam.” arXiv:1109.4897v1 (2011)
[2] Vongehr, S.: “Supporting Abstract Relational Space-Time as fundamental without Doctrinism against Emergence.” arXiv:0912.3069v2 (2009)
[3] Liberati, S., Sonego, S., Visser, M.: “Faster-than-c Signals, Special Relativity, and Causality.” Annals of Physics 298, 167–185 (2002)
[4] Vongehr, S.:"Improving Modal Terminology via the Historical Parallel and Deeper Connection between Einstein’s and Everett’s Relativities" under review, to appear soon on arXiv (2011)
--------------------------------------------





Comments