Frederick II (1194 –1250), Holy Roman Emperor and King of Sicily, so I have read, preferred equation-solving contests to watching knights impaling each other in jousting. Certainly, the great mathematician we know today as Fibonacci spent some time at his court.
As a result of this development, Italy became a leading centre of the mathematical arts, and by the 1530s the solving of cubic equations was all the rage in Venice, with great prize money. In 1535 a spectacular victory was scored by Nicolo Tartaglia (1500 –1557). He was persuaded by Gerolamo Cardano (1501 –1576) to divulge the secret. Cardano developed the method further, and in 1545 published his Ars Magna (great art) of solving equations, which resulted in a bitter dispute with Tartaglia.
What is significant here is that Cardano is the first on record to stumble across complex numbers as a necessity in the algebraic solution of some cubic equations – indeed cubic equations with three real roots always require their use, and to these he gave the name irreducible. Solving a particular cubic equation, he writes:-
Dismissing mental tortures, and multiplying 5 + √ –15 by 5 – √–15, we obtain 25 – (–15). Therefore the product is 40. .... and thus far does arithmetical subtlety go, of which this, the extreme, is, as I have said, so subtle that it is useless.
Cardano was also an inveterate gambler, and from 1525 he started compiling the first proper study of the theory of probability, which was only published posthumously in 1663 as Liber de Ludo Aleae (Book on Games of Chance).
In the May 2009 edition of Physics World, the has appeared an article The Gambling Scholar (well worth a read!) by Artur Ekert. Ekert is a leading worker in quantum computing, and holds simultaneous professorships in Oxford, Cambridge, and Singapore. In this article he shows how Cardano founded both of the mathematical pillars of quantum mechanics, namely complex algebra and probability theory. Cardano was the first to state that, when enumerating different throws of say three dice, a sequence of 2,3,5 is to be counted as distinct from 3,5,2 or any other permutation.
Those who do A-level maths at school learn that the combined probability of one or other of two mutually exclusive events occurring is the sum of the individual probabilities. However, in the quantum world it ‘don’t work that way’. Probabilities have to be added according to complex arithmetic, with a phase angle thrown in to boot. (Someone who works in this field might like to explain this properly in a comment.)
In a 1999 paper Machines, Logic and Quantum Physics arXiv:math/9911150v1 , David Deutsch and Artur Ekert, together with Rossella Lupacchini of the Dipartimento di Filosofia, Università di Bologna, show us how this lies at the basis of the remarkable potential of quantum computers. In the picture there are two identical machines (the word is being used as in ‘Turing machine’) which, when tested separately, behave as a random switches. However, if placed in sequence 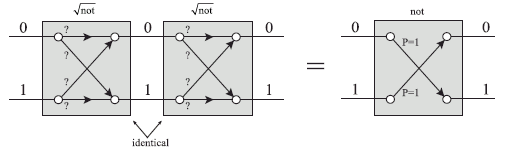 the pair will function as a simple NOT gate. Therefore, as individual machines these are behaving as the square root of NOT.
the pair will function as a simple NOT gate. Therefore, as individual machines these are behaving as the square root of NOT.
The authors continue
It may seem reasonable to argue that since there is no such operation in logic, the √not machine cannot exist. But it does exist! Physicists studying single-particle interference routinely construct them, and some of them are as simple as a half-silvered mirror.
.gif)
So why is Cardano not the popular hero he deserves to be? In the case of probability, the answer is simple. By the time his Liber de Ludo Aleae was published, Fermat and Pascal had already taken the field. Probability theory then forged ahead, with great names such as Abraham de Moivre (1667 – 1754) blazing the trail.
Complex numbers had a much more difficult passage, and did not really ‘make it home’ until the work of Euler planted them firmly on the mathematical map. But to my mind, the villain of the piece is the great philosopher Descartes. The problem with great philosophers is that when they start to speculate, their followers form a pressure group which excludes alternative ideas. It took two thousand years before Galileo dealt the death-blow to the physics of Aristotle. Descartes, in this respect, is a multiple offender, in optics squashing for a time the wave theory of Huygens with Fermat’s corollary that light would travel more slowly in a dense medium. But it was he who invented the term imaginary number which has caused confusion ever since. (In fact, Leibniz, taking up this usage, seems to have invented the term real number.)
What was the root of Descartes’ error? It seems to be that he carried his cogito ergo sum a bit too far, and said "I can’t think of them, therefore they don’t exist". Alas, disputing with philosophers can be an exhausting task. As my father used to say, "they could argue the hind legs off a donkey".
My own defence in such circumstances would be that of Pepé le Pew:

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *





Comments