Tackling the problem of spam is a problem in communication. If spam is noise as against wanted communications, then the spam problem is a signal to noise filtering problem. Unwanted emails, especially broadcast spam emails, consume about 80% of currently available bandwidth. We need to filter out the 80% noise so as to increase the efficiency of the web in distributing the 20% of traffic that is the wanted signal.
In using the internet we find spam in various forms. The most widely known is the spam email. Less widely known is comment spam. Comment spam takes many forms. Usually, a comment is made on a blog or forum which appears to be innocuous, something on the lines of "Nice article." or "I agree." The primary hallmark of comment spam is that it contains one or more links to commercial websites. The secondary hallmark of comment spam is that it is most frequently 'content free', i.e. it adds nothing to the discussion. A favourite tactic of the comment spammer is to place a url in the spammer's profile. Frequently, a site moderator will delete the comment but leave the profile.
A small piece of code in a comment or spam email, and to some extent the spammer's url is used by spammers as a beacon. The persistence of the beacon code is used by 'spammer kings' as a measure of the economic costs of placing further comment spam on that particular web site.
The Bandwidth Problem
It is not generally realised that spam filters operate on a mail server or on a user's computer only after the spam emails have been dispatched. In order to reach the filter, the spam must first travel over the backbone of the web. The fact that a well-protected individual user receives little spam should not be taken as in any way related to the network bandwidth consumed by global spam.
If we use the term 'webspam' to refer to all of the variants of spam, then it is easy to determine that at least 80% of bandwidth is used by spam.
One of the methods used by spammers is the faking of the source of the spam. Most email users do not know how to analyse email headers to determine the real source. Indeed, most email reader programs do not show the full header.
Whilst individual users may have reason to use email encryption, most users communicate using plain ASCII or HTML script. Such messages are easily faked. I propose an automated encryption scheme whereby security of communication is combined with source verification in such a way as to counter the source faking and scatter-gun methods used by spammers.
Alice, Bob and Carol
It is traditional in cryptology to use the names Alice, Bob and Carol. These are merely more readable substitutes for the letters A, B and C. The use of these names should not be taken as implying that a particular encryption method requires human intervention, or even communication. When 'Alice' communicates with 'Bob', these may be computer programs which are hand-shaking in a communications network such as the internet.
The basis of all encryption is the need to ensure that Alice and Bob can communicate secretly and that it is computationally infeasible for Carol, an eavesdropper, to either read a secret message or insert a fake message.
This could have a real-world application in spam filtering: Alice and Bob can reject any unauthorised message by proving a lack of authentic origin. If a method could be found by which every 'Alice' on the web could use such a blocking filter, the effective bandwidth of the web could be increased.
The Padlocked Box
Ordinary encryption of a message can be modelled as placing a message in a locked box. If Alice locks a message in a box, and Bob has a key to that padlock, then they can communicate secretly. It should also be obvious if the box has been tampered with by Carol. The chances of Carol creating a fake box which is locked with an identical padlock are remote.
The problem is, how does Bob get the key? If Alice wants to broadcast a message, then she has to send out a lot of keys by a secure means. This adds costs, and there is always a risk of key interception. That is a fundamental problem in cryptology: the key distribution problem. How do you prevent Carol from getting hold of the key and copying it? One method is to have a padlock which can be secured by snapping it shut, but only unlocked with a single, private key. Alice makes these locks publicly available, but keeps the key private. In effect, one may think of the padlock as being locked by a public key and unlocked by a private key.
The inherent problem with a public key - private key model is that the fact that one component is public gives a means of attack. Analysis of the public component is a step towards determination of the private component. Carol has a lever with which to crack the box open.
Mathematical public-private key methods rely on the use of large prime numbers. The security of the method relies on the computational infeasibility of determining the exact numbers used, that is, even using the fastest computers, cracking the code takes ridiculous amounts of time. However, an attack remains computationally infeasible only for so long as there exists no known method for the fast determination of prime numbers. If a new discovery were made in prime number theory, many encryption schemes would be immediately rendered insecure.
The Multiply Padlocked Box
In order to remove the need for a public key, Alice and Bob could use a box with a locking mechanism which can accomodate more than one padlock. Alice locks a message in a box and send it to Bob, who adds his padlock and returns the box. Alice removes her padlock and sends the box once more to Bob. Bob can now unlock the box and read the message. Carol cannot access the contents of the box. If Carol creates a fake message and sends it to Alice, Alice will add a lock and send the box 'back' to Bob. Bob sees a box with two locks, neither of which he can open, so he determines that the message is fake.
The problem with real encryption has been that encryption is a LIFO problem. However many times a message is encrypted, the last encryption put on must be the first encryption taken off.
A mathematical solution to the multiple padlock problem must allow for the encryption layers to be taken off in at least reverse order. This is the commutative encryption problem. An ideal solution would allow for encryptions to be removed in any order.
A proposed Method For Commutative Encryption
The message to be encrypted is arranged in an array of N dimensions. This might be visualised as a page, a folio, a book, a set of volumes, a shelf, a library etc. For each dimension, a communicator can create a completely private key and use it to add an encryption scheme which does not affect the other dimensions. In the case of two communicators, Alice and Bob, Alice could encrypt all odd dimensions whilst Bob could encrypt all even dimensions. It may be seen that shuffling pages in a book does not affect the page contents, and shuffling of page contents does not affect page sequence.
In this dimensional transpositionally encrypted model, there are two advantages: no key is exchanged, and the network location of each transmitter is verified during exchanges. Suppose that Carol sends a message with a faked header to Bob. Bob will be recrypt the message and send it to Alice, the purported original sender. Since Alice has no record of the message, she determines the message to be fake, she destroys it and sends a message to Bob so that Bob can destroy his unwanted key.
A demonstration in two dimensions.
This demonstration uses a message formatted in two dimensions, as it might appear on a sheet of paper. The encryption scheme used for demonstration is roughly character, or byte sized. In practice, the message would first be padded and compressed so as to disguise its inherent structure. It would then be encrypted using variable size slices.
The method is demonstrated using a sheet of paper which has been coloured to help keep track of the rows and columns. The scrambling has been minimised for clarity. In a real application, more than two dimensions would be used.

The message is first scrambled in the x dimension by Alice. In practice, the key would be an array of slice widths with their original locations. The key contains no data from the message and is entirely private.
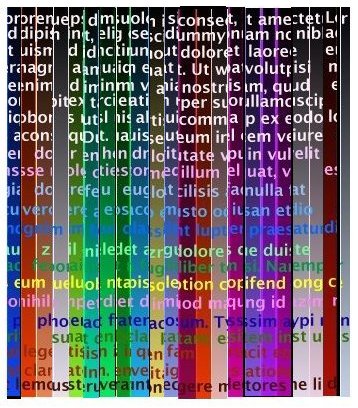
Bob keeps a copy of the x-scrambled message and sends a y-scrambled copy to Alice. Again, the private key is an array of slice widths with original locations.
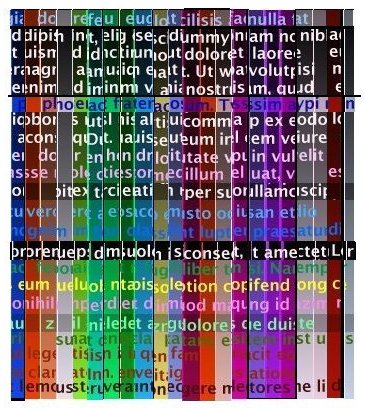
Alice descrambles the x dimension and returns a copy which is now scrambled only in the y dimension. Bob descrambles the y dimension and retrieves the original message.
In practice the message could be any data. It is padded as needed and then compressed. The padding data is chosen so that the message + padding when converted to binary gives equal counts of 1s and 0s. The compression algorithm is chosen so as to make the transmitted data appear more randomly distributed before the encryption scheme is applied.
By creating a different key for each odd dimension, Alice can multiply encrypt the outgoing message in a method that is as computationally secure as a one-time pad. Similar considerations apply to Bob's multiple encryption in the even dimensions. Each applied encryption is done using a key generated at the time of use and destroyed after being used for decryption. In effect, the data is encrypted using a one time pad for each dimension of encryption.
It is important to note that the communicators must not encrypt any single dimension twice. It is only by encrypting separate dimensions through transposition of 'strips' that the method is independent of encryption sequence.
A practical application
Such a method could be used in an email communications sytem. Because of the need for the communications programs to handshake, it is necessary for an email sender to provide a genuine return address. Although the system as described needs three passes to send one message, that message might contain a secret one-time pad for a batch of follow-up messages. This would reduce the bandwidth overhead. It must be remembered that currently 80% of network bandwidth is used by spam. By blocking spam, even if every single message were to be sent three times, there would be a net freeing up of bandwidth.
Footnote:
I have chosen to make this theoretical model of a commutative encryption scheme public in order to stimulate research into commutative encryption and to make the model available for real world testing and possible implementation as open source code.
Recommended reading:
Wikipedia Cryptography
Cryptology by Oliver Pell
This topic is continued in Bootstrapping Commutatively Encrypted Communication





Comments