Might it be possible to harness our visual computational powers for other tasks, perhaps for tasks cognition finds difficult? I have recently begun such a research program with the goal of devising ways of converting digital logic circuits into visual stimuli – “visual circuits” – which, when presented to the eye, “tricks” the visual system into carrying out the digital logic computation and generating a perception that amounts to the “output” of the computation. That is, the technique amounts to turning our visual system into a programmable computer.
This is not the first time scientists have attempted to make use of biological computation; this was first tried with DNA, tapping into the computational prowess inside cells. My research is the second kind of biological harnessing that has been attempted for computation, aiming to commandeer our very brains. Because this new kind of computation – “visual computation,” or “eye computation” – is carried out in people’s brains, its outputs can be directly and immediately fed into humans, making for true human-computer interaction, all in one head!
Why with the Eye?
People are notoriously poor reasoners, whether in the probabilistic domain or logical domain, something I have also personally witnessed when teaching logic and computer science. That’s one of the reasons we all appreciate computers. Although our reasoning and logic powers are poor, we are all walking around with computers in our heads that are far more powerful in many respects to any computing device ever built, or likely to be built in the foreseeable future.
There are several reasons why the visual modality is a promising one for biological computation. First, the computations underlying our elicited perceptions are extraordinarily powerful, our visual system taking up about half our cortex. Second, our eyes and visual system are capable of inputting and processing large amounts of information in a short period of time. Third, in spite of the billions of calculations carried out at each glance, it feels effortless to perceive. Fourth, visual neuroscience is by far the most well understood subfield of neuroscience, both at the level of neurobiological mechanisms and perceptual phenomenology. Finally, visual stimuli are a much easier modality for presenting stimuli – e.g., on paper – whereas audition, say, requires a computer or play-back device.
The idea of tapping into vision for computation is not new. Mathematical notation itself is a visualization technique and aid to cognition. The invention of writing, more generally, moved language from the auditory modality to a visual one, and enhanced our reasoning capabilities.
Visualization within science in the form of graphs, charts, etc. has been crucial for understanding complex phenomena. Visualization has also been employed for over two hundred years in logic.
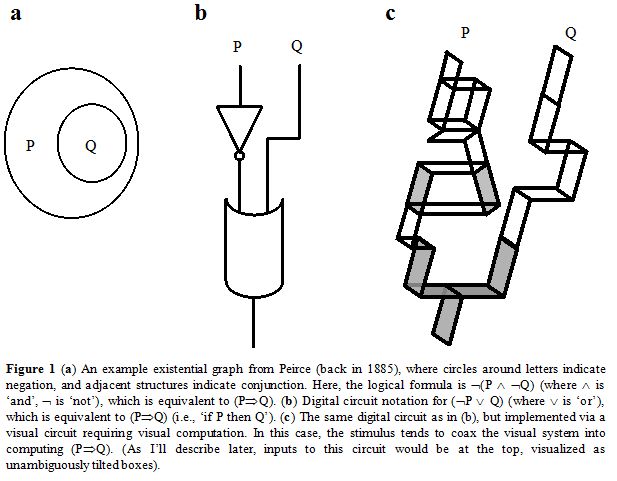
For example, Leonhard Euler invented diagrams to visually represent the contingent relationships among concepts, John Venn utilized visual diagrams to show the logical structure relating concepts, and Charles Sanders Peirce invented existential graphs (Figure 1a) for depicting logical formulae. For digital logic there has long been a standard visual notation scheme that depicts each logical formula as if it were a physical electrical circuit, as shown in Figure 1b. Figure 1c shows a preview of the kind of visual circuit I have been designing; we’ll see more of these later.
Vision has, then, long been harnessed for computation, in particular with the aim of facilitating human reasoning.
The “visual computation” technology I am designing is something altogether different. The aim is not simply to use visual stimuli to aid one’s cognitive computations. Rather, the aim is to get our visual system itself to obediently carry out the computations.
The broad strategy is to visually represent a computer program in such a way that, when one looks at the visual representation, one’s visual system naturally responds by carrying out the computation and generating a perception that encodes the appropriate output to the computation. That is, there would be a special kind of image that amounts to “visual software,” software our “visual hardware” (or brain) computes, and computes in such a way that the output can be “read off” the elicited perception.
Ideally, we would be able to glance at a complex visual stimulus—the program with inputs—and our visual system would automatically and effortlessly generate a perception that would inform us of the ouput of the computation. Visual stimuli like this would not only amount to a novel and useful visual notation, but would actually trick our visual systems into doing our work for us. Other visual notation systems for logic and computation – such as Charles Peirce’s “existential logics” or standard digital circuit notation (see Figure 1a and 1b above) – cannot do this.
Escher Circuits
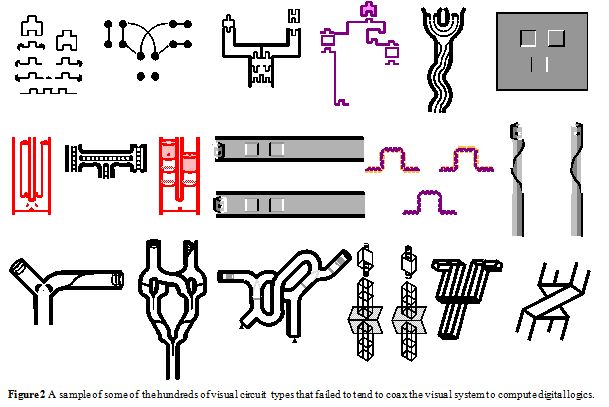
In my attempt to hack into our visual system and program it as I wish, I have experimented with hundreds of varieties of visual circuit instantiations, for much of that time with little success.Figure 2 illustrates some of the broad classes of visual circuit types that failed for any of a number of reasons. Stimuli that were not successful include: (i) cases where the bistability was figure-ground (and for these circuits a large problem was that the “wire” was not “insulated,” and would quickly leak and spread everywhere in the circuit), (ii) some stimuli looked like pipes and tubes (but although NOT was easy to achieve, AND and OR were not even conceivably computed), (iii) some kinds of circuits tried to affect the probable illumination direction, thereby modulating the perceived convexity of a bump/crater, (iv) some utilized dynamic stimuli with dots alternating positions, with ambiguous motion signals, (v) others had a similar idea, but for grouping ambiguously grouped pairs of objects, and (vi) color spreading was utilized in some attempts.
Finally, though, I found a variety of visual circuit that (kind of) works. The design relies on depth ambiguity, and was the first design that enabled perceptual AND and OR operations, as well as satisfying the other early constraints for the simplest digital visual circuits. Because this variety of visual circuit can often look vaguely Escherian, I call them Escher circuits.
To understand Escher circuits, we must start with the most fundamental part in them: wire.Wire: Circuits need wire in order to transmit signals to different parts of the circuit, and an example case of “visual wire” is shown on the left in Figure 3. It is bistable, and can be perceived either as tilted away (0) or tilted toward you (1). Stimuli of this sort serve as wire because your perception of its tilt at the top propagates all the way down it to the bottom. This kind of stimulus also serves as insulated wire, because state changes tend to be confined to the wire itself. Many circuit varieties I experimented with before the current variety suffered from leaky wires, where the state would spread across the page: for example, this was a key problem when trying to use figure-ground perceptual ambiguity for digital state. In this style of Escher circuit, wire has a canonical form, directed down and to the left as in the orientation shown at the input and output of the wire on the left in Figure 3.
Wire can also be bent as in the case shown, which – with the increased junction information – can make the perception of depth more pronounced and stable. But these circuits are designed so that any such bends must eventually “unbend” when being input into another component of the circuit. This feature of visual circuits is important in understanding the design difficulties in building a NOT gate, something I’ll discuss in a moment.
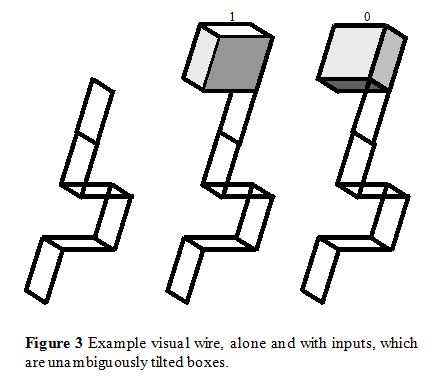
Inputs: An input to an Escher visual circuit is an unambiguous cue to the tilt at that part of the circuit. Here I utilize simple unambiguous boxes as inputs, as shown in Figure 3 on the middle and right. One advantage to inputs of this kind is that differential depth cues lead to pop out: in larger circuits there will be many inputs, and it will be crucial for the pattern of tilt-towards and tilt-aways – i.e., the binary input – to stand out as a perceptible pattern so that it can induce the computations in the circuit.
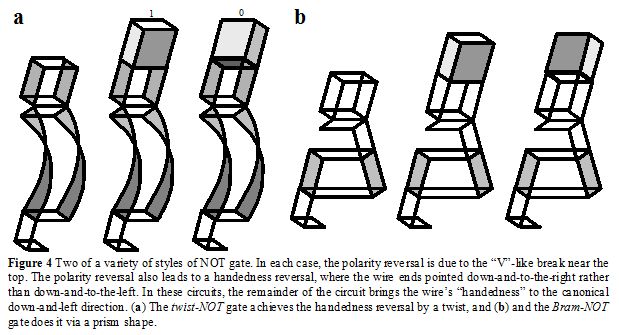
Negation: NOT gates are crucial for digital circuit computations, inverting the signal from a 0 to a 1 or vice versa. Figure 4a shows one kind of visual NOT gate for Escher circuits. It begins as a special kind of wire—roughly a wire-frame box—which undergoes a “break” below it. The portion of wire below the break tends to be perceived as having the opposite tilt to that above the “break.” The curvy portion below it is required here in order to bring the wire back into the down-and-leftward canonical orientation for wire in these circuits. Another variety of NOT gate is shown in Figure 4b, this one relying on an ambiguous prism-like shape to correct the circuit orientiation, or handedness. A third type is inside the circuit shown in Figure 6.
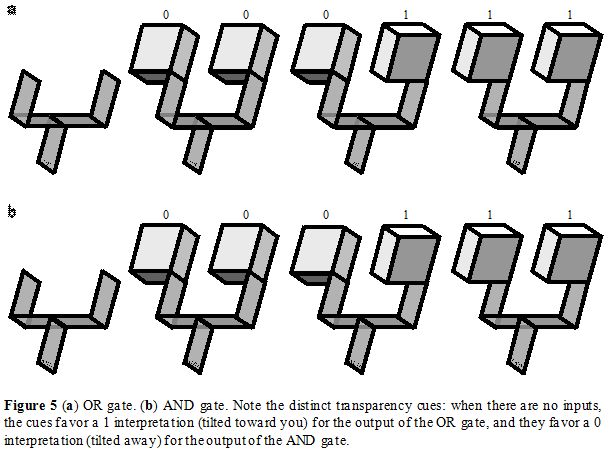
Disjunction and conjunction: Escher circuits allow ORs and ANDs as shown in Figure 5. The visual OR gate in Figure 5a is designed with transparency cues so that the tilted-toward-you, or 1, interpretation is favored, and tends to be overridden only when both inputs are 0s. A similar idea works for an AND gate, but with a distinct kind of transparency cue. That is, the OR and AND gates are designed so that, without inputs, 1 and 0 output interpretations are favored, respectively.
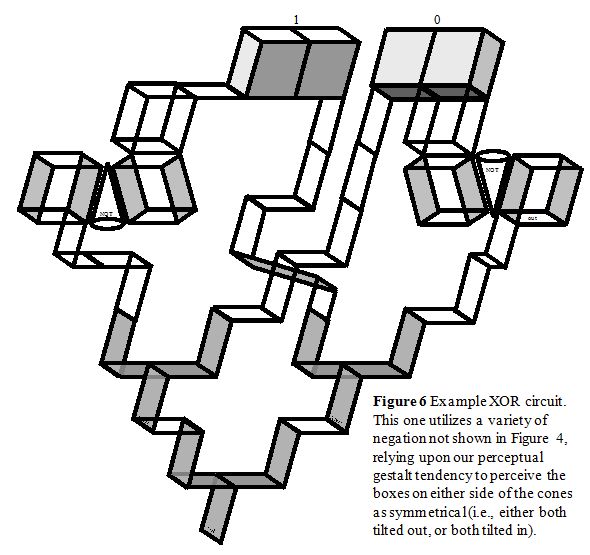
These gates – NOT, AND, and OR – are sufficiently powerful that any digital circuit can, in principle, be built from them. (In fact, {NOT, AND} and {NOT, OR} are each universal.) In the circuit shown in Figure 7b are two NAND gates (relying on similar transparency cue tricks as for OR and AND), and a NAND gate is, by itself, universal. Figure 6 shows an example larger circuit, an exclusive-OR (XOR).
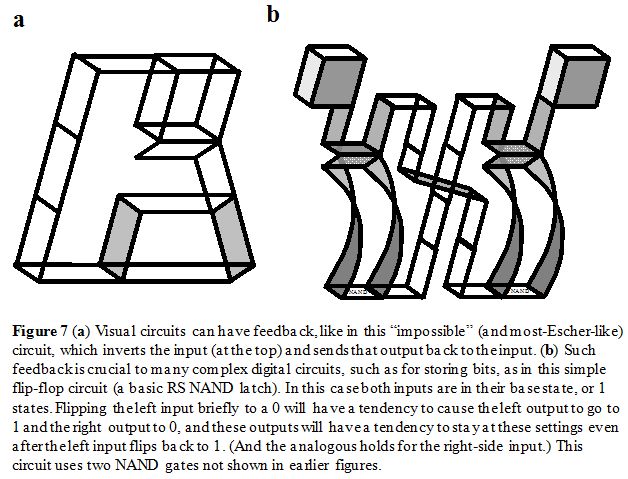
Most of the interesting computations possible with digital circuits require feedback, and Figure 7 gives two examples, including a simple variety of flip-flop for memory storage.
What’s the Point?
Why do any of this? I can imagine a variety of possible long-term benefits (some of them quite fantastic).
Enhanced computation: One general potential payoff concerns the possibility that some programs could be run more quickly on an “eye computer” than on an electronic computer. These would be programs that critically rely on the visual system’s specialized “GPU” (graphical processing units), something unparalleled by computational vision algorithms. This is analogous to the original hopes for DNA computation.
Computation that interacts with the brain: DNA computation did not end up useful for carrying out computations faster than electronic circuits. Instead, it was realized that the advantage of molecular computation was that it allowed the direct communication and interaction with the cell biology. Analogously, whether or not eye computation can ever be employed to carry out computations more efficiently than on an electronic computer, the benefit may be that visual circuits can directly interact with the neural machinery – because the neural machinery is the computer here.
State-dependent perceptions in static stimuli: One of the directions of interaction can be from brain to computation, where different observers – having different brain states – may react differently to a certain visual circuit. For example, one can imagine a circuit component whose perceptual resolution is modulated by the observer’s, say, thirst (actually, there are such stimuli, something from 2001 research of mine). The visual circuit would be designed to communicate (via its perceptual resolution) something relevant for thirsty observers when thirsty, and something else for non-thirsty observers.
Diagnostic Rorschach-like tests: One of the hopes of molecular computation is to have molecular computers that can interact with cells, and whose output will depend upon the state of the cell. In this way, molecular computation hopes to be a diagnostic tool. Similarly, eye circuits may potentially have value as a diagnostic tool for neurology and psychiatry: the patient reports the perceptual output to the doctor, and this output is diagnostic about which condition the patient likely has. Like a Rorschach inkblot test, eye computation relies upon ambiguity; but unlike Rorschach tests, visual circuits carry out specific algorithms, and can be explicitly designed.
Treatment: The other direction in the brain-computation interaction is from computation to brain. For molecular computing, the idea would be that the molecular computer can selectively affect the cellular environment. For eye computation, the goal would be to develop circuits that can leave a particular lasting impact on the visual system and brain. Just as with flip-flop circuits it is possible to create and control a long-lasting state change (used for memory storage), visual circuits can potentially induce perceptual states, and in such a way that even once the input stimulus inducer is removed, the perceptual state remains “frozen in”. There may, then, someday be routes by which visual computation could not only diagnose psychiatric and neurological disorders, but also be involved in treatment.
Programmable perceptions: Visual computation could provide powerful tools for manipulating an observer’s perception, despite much or all of the visual stimulus remaining identical. For example, a three input visual circuit can have up to eight different perceptual states, and which perceptual state the observer is in can be controlled by modulating the three unambiguous input visual stimuli. It is also possible to program for arbitrary kinds of perceptual ambiguity: for any visual circuit without inputs, one’s perceptions will tend to settle only on the logically satisfiable solutions to the circuit, and so one can purposely engineer which of multiple perceptions are possible for a viewer.
Enhancement of human logical capabilities: Despite the presence of computers, people rely more and more on visual displays aimed at aiding our thinking. For example, digital circuit notation is used more than ever among engineers, and visual notation for mathematicians and scientists is likely to always be with us. Visual computation makes new inroads into visual displays, and radically extends its horizons so that the visual modality is not just a medium for the iteraction of vision and cognition, but lets loose the computational dynamics of the visual system. For example, rather than an engineer programming digital circuits via thinking his or her way through traditional digital circuit notation, with visual circuits the engineer’s visual system will be harnessed and allow him or her to much more quickly see – literally see – the computational steps.
Manipulation of perceptual memory: Manipulation of computer memory (in RAM) relies upon digital circuits like flip-flops, where a brief signal to one of the inputs leads to a state change (a bit flip) at one of the outputs, and this new state remains even after the brief input signal is removed. Such digital memory circuits can be implemented via visual circuits as well, allowing a short presentation of an input stimulus to cause a long-term shift in the perceptual output. Circuits like this rely upon feedback, which in the case of visual computation amounts to one’s own perceptual state being fed back to earlier parts of the circuit, affecting the perceptual state there. I foresee memory circuits such as these eventually being crucial building blocks for visual circuits, helping to maintain greater circuit perceptual stability. In the long run one hope would be that visual circuits for bit storage could be utilized as an aid to working memory, allowing us to artificially enhance our working memory limits by tapping into visual working memory.
Mnemonic device: One common technique for enhancing recall is to create imagery connected to the list of terms to be recalled. The imagery is more easily recalled than the list all by itself, and the imagery then helps one recall each of the terms. Visual computation allows something like this. The list of terms to be recalled is now the input to a visual circuit, and the visual circuit is designed so that there is a one-to-one correspondence between the possible inputs and the resultant visual circuit perceptual state. The list of terms now computationally induces a particular imagery, and the person just needs to remember the look of the induced imagery. To recall the list, the visual circuit is presented without inputs, the observer recalls the imagery, the imagery helps induce the visual circuit into the earlier perceptuo-computational state, and this state leads to perceptual states at the inputs (now empty), which can be read off one’s perception to attain the original list.
Just the Beginning
Although the Escher visual circuits I just described are a great improvement over my many earlier attempts (see Figure 2), there are serious technical difficulties to overcome.
First, the larger circuits currently appear to require – at least without training -- “perceptually walking through the circuit” from the inputs downward toward the output. One does not yet immediately and holistically perceive the output. Second, the visual logic gates do not always faithfully transmit the appropriate signal at the output. For example, although AND gates tend to elicit perceptions that are AND-like, it is a tendency only, not a sure-fire physical result as in real digital circuits. Third, even if a logic gate works well, in the sense that it unambiguously and robustly cues the perception at the output, our perception can be somewhat volatile, capable of sudden Escher-like flips to the alternate state. The result is that it can be difficult to perceive one’s way through these visual circuits. And, fourth, building larger and more functionally complex circuits will require smaller and/or more specialized visual circuit components in order to fit the circuit on an image (analogous to the evolution of electronic circuits).
A major problem to overcome is how to do this while still ensuring that the visual system reacts to the circuit as intended.
The current visual circuit design is only the first step, demonstrating the basic concept. It should be thought of as analogous to the early research stages in DNA computation, an idea that was “miles away” from the ideal promise at the inception…and still is.





Comments