The awareness that there is also this other force field leading to closed elliptic trajectories came to me during my lecture in optics. Optics is not directly my main field and we were going through notes written by my colleague who really is an optics expert. However, the analysis of elliptic polarization of light and the ellipses occurred very complicated to me, so I asked the students if they knew anything about the Lissajous patterns (wikipedia.org/wiki/Lissajous_curve). Some did, but not all. So I tried to recollect the details, but I then referred to the next lecture. Especially the part about positive or negative phase shift was a bit unclear to me, so immediately after the lecture I wrote that little "simulation", i.e. the plot of the pattern, but with two stars chasing each other to show in which sense the pattern is drawn. And sometimes during this I realized that this is the trajectory in the combined oscillator field.
Why is this interesting - in 5 steps
1. First of all, for the fact already mentioned. We have the well known force field described by radially symmetric potential energy V( r )=-C/r,
i.e. the Coulomb or gravitational field, leading to stable closed ellipses, but also the isotropic oscillator field
V( r ) = k r^2
in addition to that. This is well known to the people working with various fields of theoretical physics where such questions may be relevant, but apparently not to everybody, including me. And not to all the students. The following two pictures are snapshots of circles and ellipses, first from the Lissajous angle (the stars are showing the motion (and they are moving at home: the small runs before the large one)
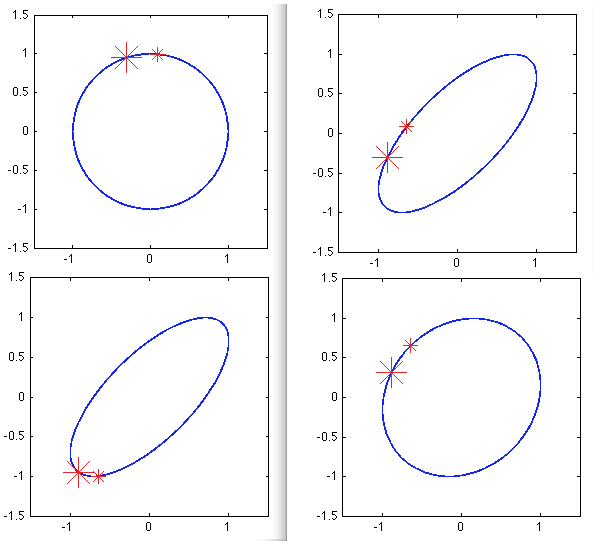
Then I added possibility of axis rotations, so the same are now brought to comfortable orientation.

2. Another aspect is that these ellipses are a special case of the Lissajous patterns, so the elliptic trajectories should occur to everybody who played with Lissajous patterns.
Since I have made myself this little plotting and animating program, I certainly played with it. In the following series of pictures I try to share some of the fun here. The functions are very simple, you can plot them in your favorite spreadsheet software
x=cos(t),
y=cos(omega t + delta)
When omega is a "nice" rational number (like 2/3 or 11/13) and delta is not zero, we get a pattern. "Best" are patterns with delta corresponding to 90 degrees, i.e half of pi. When delta is zero, we get a straight line. Taking omega as e.g. 2/3 + 0.01 the trajectories are not closed and "fill" a certain area. Lots of space for amateur research. Look at wikipedia's presentation (wikipedia.org/wiki/Lissajous_curve)



3. Third, knowing all this one can skip the analysis of elliptic polarization in physical optics. It is just the same as the two aspects already mentioned. For students who experience this the elliptic polarization and related phenomena in optics are simply a somewhat boring case of Lissajous pattern.
This is one more of the demonstrations about the power of mathematics, or is it mathematics? One pattern of behavior occurs in many different phenomena. Consequences for teaching are unclear - should we study different patterns first - and expect that learning of real physics would then be simpler? Or what about this: whenever we meet a "pattern", tell the students about all other fields where the same or similar pattern occurs? At least in textbooks? That might be a good strategy, but what if we do not know about this? As I did not know? Fortunately, we have both Wikipedia http://en.wikipedia.org/ and Wolfram's sciences scienceworld.wolfram.com/physics/. What is missing is about 36 hours per day.
4. I mentioned my little disappointment about students and computer graphics. I prefer to use matlab or its free equivalent Gnu Octave, but I could make the drawings in about twenty different ways. What surprised me that the physics students of 2011 are not at all enthusiastic about enjoying the computer graphics and when asked did not name twenty ways to do it, mainly pretended not to be able to do it at all. What most people probably can do is to put the two lines above into their favorite spreadsheet software, which in my case would be LibreOffice or gnumerics, for many others it would mean the not so excellent excel. It needs very little practice, but some little amount of enthusiasm to make quite beautiful graphics with programs lying everywhere.
5. But now, since we know that we can superpose electromagnetic waves, we could send a wave along z-axis polarized in x direction, and another wave polarized in y-direction with frequency say 2/3 of the first. Then the resulting field would be described by a pattern on the following picture:This is definitely possible to realize with many types of electromagnetic waves, microwaves, etc. The fields can be superposed, so one can look at them as independent fields - or as one combined field. But what about photons? Three of one type have same energy as those of the second type. Would there be a possibility of a mixed type photon? Here is more space for original research and lots of discussions below.
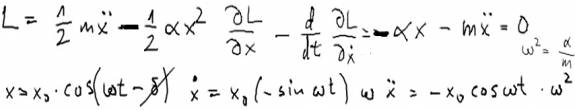


Comments