What is nonlinear optics?

Nonlinear optics is a branch of optics which studies the nonlinear interactions of electromagnetic radiation and the media. The nonlinear interaction, which means the matter responds in a nonlinear manner to the incident radiation fields, endows the media a characterization to change the wavelength, or the frequency of the incident electromagnetic waves. Typically, this nonlinear interaction only observed at very high intensity (electric field) of incoming light. Figure 1 shows the schematics of linear and nonlinear interactions of waves and the media [1].  

Fig. 1 Linear (left) and nonlinear (right) interactions of waves and the media [1].

Physical explanations

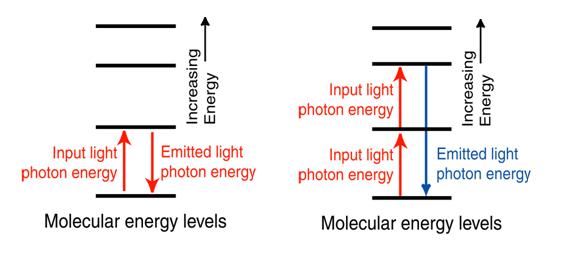
To explain the physics in Fig. 1, I would like first to show the energy diagram in Fig. 2. The molecular emitted light with the same energy as the input light under weak beam, and thus we obtain the same waves for linear optics. However, under high intensity of light, the excited photons in the matrix can be excited to higher energy level, and emitted light with higher energy than the input light energy. This is nonlinear optics, in which new waves have been created.

 

Fig. 2 Energy band diagram of linear (left) and nonlinear optics (right) [1].

The induced polarization of a matrix under an electric field can be calculated from Maxwell equation [2]. At a low field (Ē), the amount of induced dipole (P) is proportion to the electric field:

P = ε₀·χ ·E    (1)

Where χ is the electric susceptibility, ε₀ is the permittivity. This is the linear response of the electric field. At a strong electric field, the induced polarization can be expressed by the Taylor expression:

P = ε₀ [χ ·E + χ₂·E² + χ₃·E³......]    (2)

χ₂, χ₃…… are high order terms which can be obtained in this condition. They are nonlinear optics. The waves from this high order terms are named as 2^nd, 3^rd …… harmonic waves, with a frequency of twice, treble….. of the incident waves.

It is well known that the nucleus is surrounded by electron clouds and the net charge of the atoms is 0 as its sphere shape. If an electric field applied, the electrons will move to the opposite direction of the field and the cloud will change its shape to ellipse. The positive and negative charges are separated and form dipole moment, which is polarization. The Eq. (1) and (2) are results of polarization calculated from Maxwell equation, and the higher ordered terms under higher field indicating the nonlinear interactions. If a sinusoidal changed electric field applied,

E = E₀·sin(ωt)    (3)

Equation (2) can be written as:

P = ε₀ [χ ·E₀·sin(ωt) + χ₂·E²·(1-cos(2ωt)......]   (4)

The second term, χ₂·E²·(1-cos(2ωt), indicating the electromagnetic waves with double frequency as the input waves. This is the second harmonic generations. For higher order terms, larger frequency can be obtained if the electron field is high enough.

Actually at a weak field we also have this higher order terms, but they are rather small comparing with the linear term and can not be observed form the optical experiments. Thus for all matrix we can obtain nonlinear optics if we have strong enough intensity of incident light.

Frequency conservation

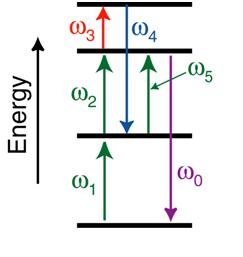
As shown in Fig. 2, the frequency (wavelength) of light can be changed by the nonlinear optics.  The energy of the photons must be equal for the input and output photons. For example, in Figure 3 there are 5 kinds of photons, ω₁, ω₂=ω₅, ω₃ (excited photons), ω₄ and ω₀ (emitted photons). According to the conversation of energy,

ω₀ = ω₁ + ω₂ + ω₃ - ω₄ + ω₅        (5)



Fig. 3 Frequency conversation.

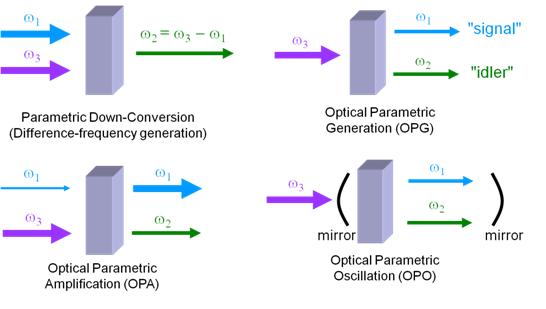
From the frequency conversation, different frequency can be obtained by second harmonic generation (SHG), optical parametric generation, amplification and oscillation, as shown in Fig. 4.  The only thing is the conserved energy of the whole system [2].



Fig. 4 The generation of different frequency.

Phase matching

Beside the frequency conversation, the momentum of the photons should also be conserved, shown in Fig. 5 for the photons in Fig. 3. However, for the obtain signal K₀ may not correspond to the light frequency of ω₀ as the chromatic dispersion (the frequency is dependent on the phase velocity). Phase matching is to satisfy both frequency and momentum conservation simultaneously.

Fig. 5 The momentum conservation.

To achieve the phase matching, birefringence can be used. Birefringence is caused by the different refractive index along directions in anisotropic crystals, as described in Ref. 3. The phenomenon is described in Fig. 6. As the refractive indices of ordinal (n_o) and extraordinary (n_e) polarized light are different, the phase can be matched for SHG as shown in Fig. 7. The value of n_e is dependent on the propagation angle, and thus we can tune it for certain frequency to achieve:

n_e (ω) = n_o (2ω)    (6)



Fig. 6 Schematic of Birefringence [3].



Fig. 7 Phase matching of SHG using birefringence [1].

Nonlinear optical devices

As I have showed some in Fig. 4, nonlinear optics can be used as amplifiers (to achieve higher intensity for certain kind of waves from another incident wave), limiters (protect weak signal from stray signals), mixer (transformed one frequency to another), multiplier (the output power is proportion to the input power), etc.. [4]

References

[1] Prof. Rich Trebino, Georgia Tech., Courseware
[2] Teresa Neves Petersen, Nonlinear Optics: on the way to pump probe spectroscopy, Nano-biotechnology group, AAU.
[3] http://www.science20.com/mei/blog/birefringence_and_polarized_light
[4] http://www.microwaves101.com/encyclopedia/nonlineardevices.cfm