This article discusses a new method of mathematical physics, self-field theory (SFT), used to analyze the atom including its nucleus. Like quantum theory, SFT can be used in many other applications across physics. Our aim in this article is to outline the basic mathematical foundations of SFT and to demonstrate its intimate relationships to the history of physics during the early 20th century. In summary we find the mathematics is a 'completion' of Bohr's theory of the electron that was discovered in 1913. The centre of the formulation is the Maxwell-Lorentz equations termed the 'Maxwellian'. This compares to the wave equations and potential theory based on the Lagrangian of quantum, theory.
In addition to a deterministic solution for the hydrogen atom, the mathematics provides a previously unknown analytic expression for Planck’s constant, an experimentally determined number found by Planck in 1900. Also found is an intimate relationship between the equations at the heart of SFT and the inequality known as Heisenberg’s Uncertainty Principle (HUP). Finally it reveals an intuitively physical version of relativity that results from the bi-spinorial mathematics of SFT. The formulation is mathematically straightforward being based on the well-known theory of eigenvalues as well as the theory of linear equations.
The seminal paper describing the complete mathematics was published in Physics Essays, Vol. 18, No. 3, 265-285, 2005. Since then there have been a wide range of physics papers concerning SFT all peer-reviewed, accepted and presented including conferences at Moscow and St. Petersberg in Russia, Beijing, Xi'an and Suhzou in China, Wroclaw in Poland, Dublin in Ireland. Cancun in Mexico, Cambridge, Washington, San Diego in the U.S. to name a few. SFT also has application to biophysics including the dynamics of the cell within the cell cycle; a number of peer-review papers and presentations have been made at the Bioelectromagnetics Society annual meetings held internationally across the globe over the past 20 years.
1. Self-field theory and its application to the hydrogen atom.
Electrical and magnetic fields have been known in mathematical form since the laws of Coulomb and Ampere were discovered over two hundred years ago. Applying to the macroscopic domain, modern atomic physics was then in its infancy. Both laws assume charge separation is a single nonlinear function, the square root of the sum of the squares of orthogonal distances involved in their separation. Within atomic and molecular theory the Pythagorean concept of distance has been utilized by both classical electromagnetics and quantum theory. Einstein’s relativity gave the first hint that in some phenomena separations in orthogonal directions do not couple but should stay as orthogonal directions. Thus electromagnetic fields in atoms consist of two fields each causing the atomic particles to rotate in orthogonal planes. Thus if charge is treated as being separated into two centres of rotation, electromagnetics can analytically solve for the atomic motions. The solution is identical to Bohr theory but with an additional rotation; Bohr's theory turns out to be 'incomplete'; this is equivalent to a missing magnetic current due to an additional cyclotron motion of the electron. Self-field theory 'completes' the solution.
At the turn of the 20th century classical electromagnetics was found to fail at the atomic level and quantum theories evolved to solve the atom probabilistically. Present-day understanding of the hydrogen atom is linked to the quantum theory that evolved during several decades of effort from the late 19th century until the late1920's. Bohr proposed a theory of spectroscopy in which angular momentum is whole numbers of Planck's quantum number h. Using Bohr's theory, spectral lines can be expressed as a quantum series, for example the Balmer series,
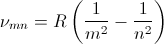
where 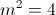
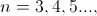 and Rydberg's number
and Rydberg's number 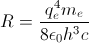 .
.
With this theory, the ground state energy of the hydrogen atom, Bohr’s energy, 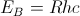 and the electron’s mean position , the Bohr radius
and the electron’s mean position , the Bohr radius 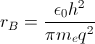 , can be estimated. Spectroscopic experiments led to an understanding of how the hydrogen atom was excited by electric (E-) and magnetic (H-) fields. By 1926, four quantum numbers n, l, m, and s had been revealed to be associated with the electron.
, can be estimated. Spectroscopic experiments led to an understanding of how the hydrogen atom was excited by electric (E-) and magnetic (H-) fields. By 1926, four quantum numbers n, l, m, and s had been revealed to be associated with the electron.
As with Bohr's theory self-field theory yields analytic solutions for the electron’s motion in the hydrogen atom as well as the well-known atomic parameters Rydberg’s number, the Balmer formula, and Planck’s ‘constant’. The fields are unconventionally measured relative to centres of motion rather than directly between charge points as in the Liénard-Wiechert potentials. In EM theory this concerns two fields and two rotations. Although there are several, this is perhaps the essential difference between the present and previous attempts to solve for the atomic motions using electromagnetics. After algebraically substituting the bispinors (to be discussed in the next section), the Maxwell-Lorentz equations result in a solvable system of spinor equations. Unlike Quantum mechanics's potentials yielding probabilistic solutions, the field variables of EM SFT allow deterministic solutions. Based on Lorentz-compatible field solutions to Maxwell’s equations, neither Special relativity nor gauge is problematic. Its field variables being a priori relativistically correct, no correction terms are required, its solutions analytic rather than numerical. In formulating quantum field theories, the EM fields are ubiquitous. In SFT a concept emerges of photon streams, two ‘pencil-beams’ mutually coupling electron and proton. The EM field is not spherically symmetric or continuous; photon streams mediate energy between particles, a discrete form of field.
2. Mathematical Heart of Self-field theory
A mathematical description for the self-fields of charged particles was first derived by Abraham in 1903 and Lorentz in 1904. This is the effect upon a moving charge of any back-reaction due to its own radiating field and the theory was found to be inconsistent with Newton’s force law. This was the first sign to science that classical electromagnetics was failing at the atomic domain. Instead of using a metric, the uncertainty principle, SFT models the field having two rotations, effectively another ordinate, meaning that the equations are now deterministic and consistent with previous results.
In general, both the particles and the EM fields that control the motions of charged particles satisfy the Maxwell-Lorentz equations. For application to atomic physics, regions where particle-field interactions occur are assumed isotropic and homogeneous and thus the constitutive parameters, 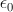 and
and 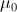 the permittivity and permeability of free-space, are scalars. Where discrete particles carrying units of elementary charge q of opposite polarity are studied, in the absence of nebular regions of charge and current density, the Maxwell-Lorentz equations can be written [i]
the permittivity and permeability of free-space, are scalars. Where discrete particles carrying units of elementary charge q of opposite polarity are studied, in the absence of nebular regions of charge and current density, the Maxwell-Lorentz equations can be written [i]
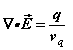 (1a)
(1a)
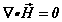 (1b)
(1b)
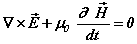 (1c)
(1c)
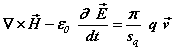 (1d)
(1d)
where the Lorentz equation for the field-forces acting on the particles is written
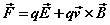 (1e)
(1e)
along with the constitutive equations 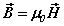 ,
,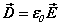 . There is arelationship between the speed of light and the ratio of the fields
. There is arelationship between the speed of light and the ratio of the fields 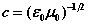 [ii]. The spatial energy density depends upon the fields
[ii]. The spatial energy density depends upon the fields 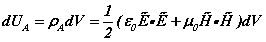 . (1a-d) are termed the EM field equations. In these equations, v is the particle velocity, m is its mass. It is assumed that the volume of integration over which the charge density is evaluated vq, and the area the charge circulates normal to its motion sq, are calculated during successive periods over which the internal motions of the atom take place (see Figure 1). As well as the motions of the atomic particles, Maxwell’s equations specify the spatial distribution of photons that comprise the E- andH-fields due to the presence of charged particles. The concept of the field andthe charged particles within it is that of a collection of smaller particles (photons) that transit between larger particles (electrons and protons). We may think of the visual capability of computers to ‘zoom’ into a displayed region. Afar, the field looks like a nebulous cloud. As we zoom in, the cloud comprising the field becomes a series of discrete point-like particles, the photons. At the same time the particles,the electron and the proton, may change their visual character from point-charges to objects with internal dynamic structure [iii]. The E- and H-fields acting on the electron forinstance are a photon exchange process between proton and electron. The fields are stream-like and exist only between particles.
. (1a-d) are termed the EM field equations. In these equations, v is the particle velocity, m is its mass. It is assumed that the volume of integration over which the charge density is evaluated vq, and the area the charge circulates normal to its motion sq, are calculated during successive periods over which the internal motions of the atom take place (see Figure 1). As well as the motions of the atomic particles, Maxwell’s equations specify the spatial distribution of photons that comprise the E- andH-fields due to the presence of charged particles. The concept of the field andthe charged particles within it is that of a collection of smaller particles (photons) that transit between larger particles (electrons and protons). We may think of the visual capability of computers to ‘zoom’ into a displayed region. Afar, the field looks like a nebulous cloud. As we zoom in, the cloud comprising the field becomes a series of discrete point-like particles, the photons. At the same time the particles,the electron and the proton, may change their visual character from point-charges to objects with internal dynamic structure [iii]. The E- and H-fields acting on the electron forinstance are a photon exchange process between proton and electron. The fields are stream-like and exist only between particles.
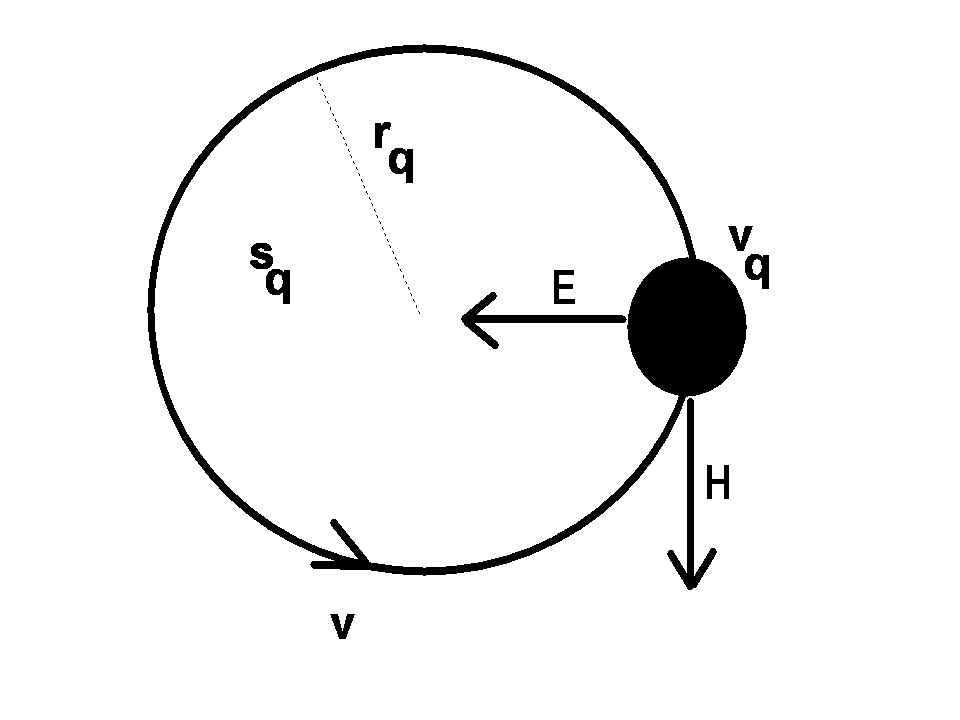
Fig. 1 A charged atomic particle moving due to E- and H-fields. Three geometric parameters are associated with the motion, the radius of motion rq the surface area sq and its volume vq
3. Solving Maxwell’s equations for atomic self-fields
Maxwell’s equations (1) can be solved to yield analytically cyclic solutions where atomic particles and their E- and H-fields perform rotations in two orthogonal but coupled directions (Fig. 3). Because this field pair induces another pair of fields this second pair can, depending ontheir speed and frequency, in turn produce the original fields. These field pairs are produced by atomic particles each performing two orthogonal motions. The overall result is a ‘self-perpetuating’ field. This approach is general in its application; recently it was used as the basis of a predicted photon chemistry where the photon, assumed to have a non-zero mass, may have an analytic ‘Balmer-like’ spectroscopic nature, but continuous rather than discrete. We turn now to the details of this analytic self-field solution for the hydrogen atom.
It is now assumed spinor forms yield the fields, forces and motions required for dynamic equilibrium. These spinors provide 'centre-of motion' E-and H-fields consistent with Maxwell’s equations. The coupled fields balance the forces of the proton and electron. The orbital and cyclotron fields control the motions of the proton and electron and vice versa, the particle motions cause the fields. We write the fields in spinor form
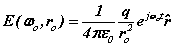 (2)
(2)
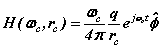 (3)
(3)
where 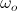 and
and 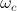 are orbital and cyclotron angular velocities, and ro and rc are orbital and cyclotron radii. The motion of the electron forms an EM self-field solution, its position is a sum of two spinors:
are orbital and cyclotron angular velocities, and ro and rc are orbital and cyclotron radii. The motion of the electron forms an EM self-field solution, its position is a sum of two spinors:
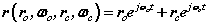 (4)
(4)
In (4) there are two spinors rotating in two orthogonal planes termed a bispinor, the orbital spinor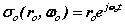 and the cyclotron spinor
and the cyclotron spinor 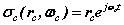 . Each spinor refers to a centre of motion; the orbital (E-field) centre of motion is stationary, while the cyclotron (H-field) rotates. This results from the coupled nature of the two spherical coordinate systems. Fig. 2 shows an actual motion. In terms of mathematical forms that lead to discrete or decoupled azimuthal modes, the complex exponential form of (4) is one such form. Solutions that return to their starting point, in other words are periodic, can maintain dynamic motions without net efflux or influx of energy. In general the various azimuthal modal forms of both kinds of rotation are a possible prerequisite to a discrete or quantum physics.
. Each spinor refers to a centre of motion; the orbital (E-field) centre of motion is stationary, while the cyclotron (H-field) rotates. This results from the coupled nature of the two spherical coordinate systems. Fig. 2 shows an actual motion. In terms of mathematical forms that lead to discrete or decoupled azimuthal modes, the complex exponential form of (4) is one such form. Solutions that return to their starting point, in other words are periodic, can maintain dynamic motions without net efflux or influx of energy. In general the various azimuthal modal forms of both kinds of rotation are a possible prerequisite to a discrete or quantum physics.
4. Principal mode of the hydrogen atom.
We first make some simplifying assumptions by specifying the problem to an 'infinite mass proton' (one that does not move appreciably, thus like Bohr we can examine the electron in isolation) and assuming the principal orbital and cyclotron frequencies are the same. After substituting the bispinorial relationships into 1(a-e), and using the virial relationships we obtain
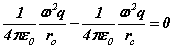 (5)
(5)
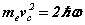 (6)
(6)
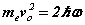 (7)
(7)
Note the rhs’s 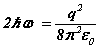 of (6-7) are known at this stage before the solution is determined analytically. Hence discrete quanta of Planck’s energy are found on the rhs’s of (24-25). These are source terms that can be traced back from the right hand sides of (1c-d). Further a connection to quantum theory is obtained. In this form, Planck’s‘constant’ is a variable of motion, dependent on the solution of the equations. The quantum nature of the electron’s motion has long been known. (6-7) reval an intimate relationship to HUP discussed below.
of (6-7) are known at this stage before the solution is determined analytically. Hence discrete quanta of Planck’s energy are found on the rhs’s of (24-25). These are source terms that can be traced back from the right hand sides of (1c-d). Further a connection to quantum theory is obtained. In this form, Planck’s‘constant’ is a variable of motion, dependent on the solution of the equations. The quantum nature of the electron’s motion has long been known. (6-7) reval an intimate relationship to HUP discussed below.
5. Solution for Electron's motion
The complete matrix equation forms two conjugate parts, for the orbital and cyclotron motions, each a sub-matrix of two equations. The principal mode case has simplified the analysis. The analytic solution can be compared with the Bohr theory expressions for the Bohr radius, resonant frequency and Rydberg’s number:
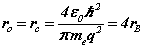 (8}
(8}
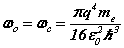 (9)
(9)
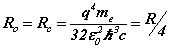 (10)
(10)
From (8) the orbital and cyclotron radii are found to be 0.5291771 x 10-10 m. From (9), the orbital and cyclotron angularfrequencies are 1.033532 x 1016 rad sec-1. If the twocomponents of energy from the electron’s motion are combined with two equal components of energy from the proton’s motion, we obtain a wavenumber 10,973,710. In this way the total system energy is linked to the motions of both the electron and proton; as the electron changes state, the motion of the proton complements any such change. THe actual motion for the electron can now be calculated as shown in Figure 2.

Fig. 2 Bispinor solution; the motion of the electron rotating in 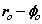 and
and 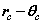 planes where
planes where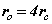 and
and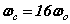 . Such a plot provides comparison with the probability densities of quantum theory
. Such a plot provides comparison with the probability densities of quantum theory
6. The proton’s motion in the hydrogen atom
We have assumed in the above that the proton has ‘infinite mass’, it is assumed not to move from the centre-of-mass and the electron moves with the entire orbital and cyclotronradius
If instead a finite-mass proton is used, the SFT equations involve both the electron and the proton. In this case, the electric and magnetic potentials become functions of the orbital and cyclotron radial distances of both electron and proton. There are six equations where the cyclotron and orbital frequencies are assumed equal. From these equations, Rydberg’s number can be adjusted giving 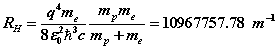 which is in excellent agreement with spectroscopic data . The proton orbital and cyclotron radii can be estimated as
which is in excellent agreement with spectroscopic data . The proton orbital and cyclotron radii can be estimated as 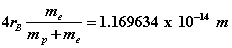 while the electron’s orbital and cyclotron radii become
while the electron’s orbital and cyclotron radii become 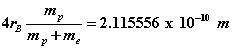 . These results are similar to the concept of reduced mass well known in Bohr’s early work. This estimate of the size of the proton is much bigger than current estimates from scattering experiments and is due to the fact that there are no strong nuclear forces in our model. The proton’s motion can be better estimated if the strong nuclear forces are explicitly included using a more refined 3-quark model (see Figure 3). In this case both EM (photons) and strong fields (gluons) are present.
. These results are similar to the concept of reduced mass well known in Bohr’s early work. This estimate of the size of the proton is much bigger than current estimates from scattering experiments and is due to the fact that there are no strong nuclear forces in our model. The proton’s motion can be better estimated if the strong nuclear forces are explicitly included using a more refined 3-quark model (see Figure 3). In this case both EM (photons) and strong fields (gluons) are present.
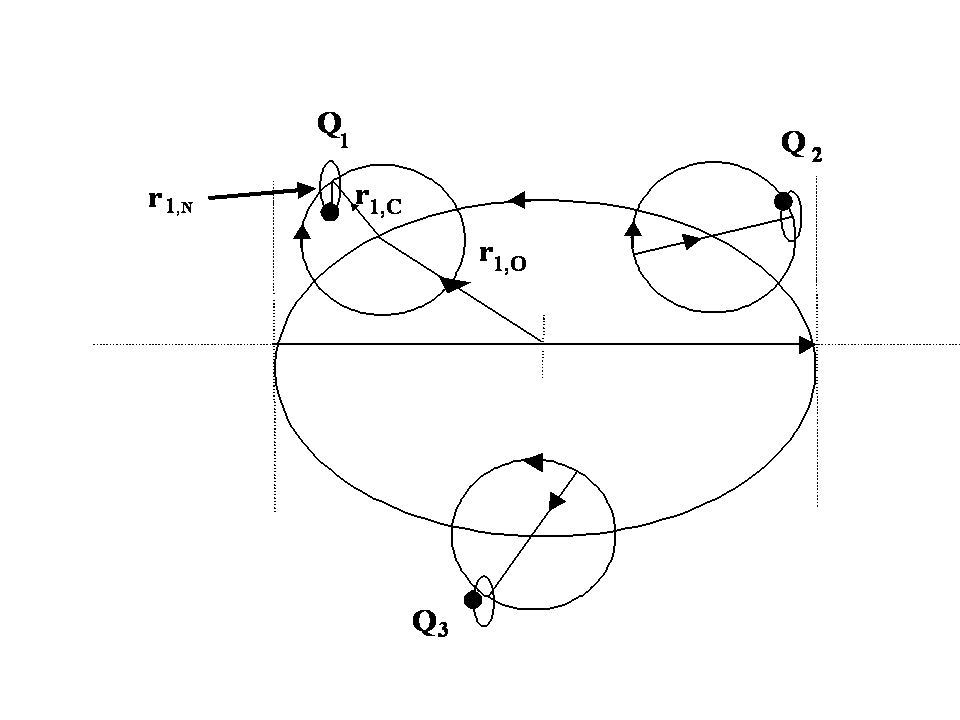
Fig. 3 Proton modelled as 3 quarks coupled via gluon fields. Both quarks and gluons have three orthogonal spinors in their motions and structure. These are termed 'trispinors'.
7. Planck's Constant
The value
of Planck's reduced constant comes from (6-7) as  and can be calculated from
the solution of the Bohr radius and the resonant frequency (8-9). Since v0
= r0ω0 = vc
= rc ωc =5.469222 x 105 m sec-1 the known
value of Planck’s constant compares with the analytic estimate to within an accuracy of 7
significant figures. It is noted that the known value of this physical constant comes from a series of experiments that have continued to the present day since Planck's Black body experiments in 1900. Thus Planck's constant can be obtained by examining the spectrum
of a black-body radiator or the kinetic energy of photoelectrons. This is is the first known analytic expression for Planck's constant.
and can be calculated from
the solution of the Bohr radius and the resonant frequency (8-9). Since v0
= r0ω0 = vc
= rc ωc =5.469222 x 105 m sec-1 the known
value of Planck’s constant compares with the analytic estimate to within an accuracy of 7
significant figures. It is noted that the known value of this physical constant comes from a series of experiments that have continued to the present day since Planck's Black body experiments in 1900. Thus Planck's constant can be obtained by examining the spectrum
of a black-body radiator or the kinetic energy of photoelectrons. This is is the first known analytic expression for Planck's constant.
8. Heisenberg's Uncertainty Principle
In the quantum mechanics proposed by Heisenberg in 1925 there was a commutation relationship between position and momentum: ![[X,P] = X P - P X = i \hbar [X,P] = X P - P X = i \hbar](http://upload.wikimedia.org/wikipedia/en/math/0/3/4/0342ffe593429f253ff09a217ad29be5.png) . HUP may be written in two corresponding forms
. HUP may be written in two corresponding forms 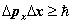 or
or
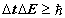 (11)
(11)
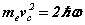 (6)
(6)
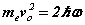 (7)
(7)
The inequality relationship of HUP (11) applies to photons, electrons, and in fact any quantum system in general. The equations for the orbital and cyclotron motions of the electron are given in (6-7) rewritten here for comparison. Apart from the ‘greater than’ relationship compared with the exact relationship, the equations are identical. Whereas there is one inexact relationship in HUP there are two equality relationships in SFT. SFT thus completes the Bohr theory that did not include any magnetic effect on the electron.
9. A Physical Way of Understanding Relativity
The bispinorial motion of the electron is given by (4) rewritten below
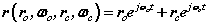 (4)
(4)
This equation applies in general to photons, electrons, and other objects across physics. If we assume it applies to a photon, we can see that if the photon has internal structure then one of these motions is internal while the other is external. Hence relativity is seen to be related to a 'hidden' motion (a 'hidden' variable) internal to the structure of the photon while the other motion is external. Our eyes manage to see the the phase of the motion and this yields the distortions we observe at high speeds.
10. Conclusions
In summary what we have shown is the intimate link between SFT and the various areas of physics that emerged in the early years of the 20th century including a reformulated version of classical electromagnetics, Bohr's theory, Planck's constant, Heisenberg's Uncertainty Principle and Einstein's relativity. There is one final connection with the past: the spinors are related to the rotating potentials used by Hertz in 1887 to show mathematically and experimentally that a half-wave dipole could transmit radio waves.
In case it be thought that this work represents a return to the past, the formulation appears fractal and involves the concept of coherent particle collisions; this is the case where photons mediate the forces between the electron and the proton. While it answers many questions, it also raises many others. For instance there appears to be a new mathematics in addition to quantum theory for treating the nucleus and perhaps new technological ways to achieve clean nuclear power.
[i] All relevant physical constants and their known values can be obtained from CODATA http://physics.nist.gov/cuu/Constants/bibliography.html
[ii] In SFT, the speed of light is not proscribed from being variable. Depending on the energy density of the region under investigation, and the photon state, c can vary inside nuclei, or in exotic places within the Cosmos. In 2007 the photon was found to have non-zero mass albeit very tiny (ca 10-55 kg 24 orders of magnitude below the mass of the electron) and hence has a spectroscopy similar to the hydrogen atom, having Balmer-like states; these photonic states are continuous due to the photon’s sub-particles having equal mass.
[iii] Photons cluster in regions of enhanced energy and can partake in the formation of high-energy nuclear particles.





Comments