[The following text is courtesy Andras Kovacs - T.D.]
This post is related to the book entitled "Maxwell-Dirac Theory and Occam's Razor: Unified Field, Elementary Particles, and Nuclear Interactions". This book is authored by Andras Kovacs, Giorgio Vassallo, Paul O'Hara, Antonino Oscar Di Tommaso, and Francesco Celani. The book's first edition is in print, and we are currently working on its second edition. After discussing our work with others peers, it became clear that we need to talk more about scientific methodology, in particular about the willingness to correct mistakes. Inspiring such discussion is the purpose of this blog post. The title applies to many areas of life, and as discussed below, also applies to physics.
Scientists like to think of their respective field as an additive process, which advances through the accumulation of ever wiser ideas and ever more elaborate concepts. That is generally true, but one must be careful to retain checks and balances and correct mistakes that inevitably slip in.
Correcting erroneous assumptions often reveals a more fundamental perspective, whereby one realizes that separate physical laws or phenomena are one and the same thing. To give an example from a pre-Newtonian era, the celestial motion of planets was accurately and predictively described by Earth-centered epicycloid formulas. The gravitational fall of bodies was accurately and predictively described by a constant acceleration formula. These two phenomenological laws were thought to be completely unrelated, and scientists of the day had no sense of any mistaken assumption: their formulas were predictive and accurate. They were the top theoreticians of the day, drawn from the same gene pool as today's theoreticians. It is safe to assume they were just as smart as the geniuses of today. But their thinking was locked into a mistaken paradigm. Once Newton's efforts revealed what the mistaken assumptions were, the phenomena of celestial motions and falling bodies were unified, although it continued to meet opposition from some who insisted that their model of Earth-centered epicycloid motions was the correct model of reality. One must understand that phenomenological formulas may involve unrealistic models of reality, even while being experimentally correct.
Correcting mistakes is an important aspect of our methodology. We list below five major misunderstandings in interpretation which we believe to have identified and corrected. We also indicate the time period since the mistake was made in both actual years as well as resource-adjusted "19th century years", abbreviated as 19C-years.
1.
Background: In the early 20th century, mathematicians discovered that the four Maxwell equations can be written as a single differential equation of the so-called "vector potential" field. The space-time gradient of the vector potential field yields three field types: electric, magnetic, and scalar.
Mistaken assumption: The role of the scalar field was not understood at the time, and it was assumed to be always zero. This assumption shows up in current textbooks as the "Lorenz gauge" condition, and it is now referred to as a "knowledge" rather than as an assumption. There are no experimental proofs for this assumption, and it was in fact shown to lead to paradoxes [1].
Age: >100 years ( >1000 19C-years).
What we discover upon correcting the mistake: Electromagnetic fields and charges are not two distinct entities - they are all part of a single vector potential field. We gain a paradox-free field theory of electromagnetism, and we no longer need to ask what charges are made of.
2.
Background: in 1927, Dirac discovered the phenomenological equation named after him, which accurately predicts the energy levels of atomic and molecular orbitals. He noted in his initial publication that this equation is a phenomenological guess and that some of its solutions appear to yield negative energy eigenvalues.
Mistaken assumption: The negative energy eigenvalue solutions of the Dirac equation became interpreted as the physical reality of negative energy states. In the high energy limit, textbooks refer to negative energy solutions as anti-particles. But electron-positron annihilation events radiate electromagnetic energy, which would be impossible if positrons were negative energy solutions. Driven by the desire to maintain the assumption that anti-particles are negative energy solutions, some textbooks engage in wild speculation about a "Dirac-sea of electrons in the vacuum" with infinite energy density, which supposedly fills the vacuum sea with electrons. According to this hypothesis, positrons are holes in the omni-present Dirac-sea of electrons. In the low energy limit, textbooks refer to negative energy solutions as "temporary violation of energy conservation", which is supposedly allowed by the Heisenberg uncertainty, and cite quantum tunneling as an example. But the mathematics of Noether's theorem clearly states that energy conservation follows from the invariance of physical laws with respect to the flow of time. Speculation about violation of energy conservation is a radical departure from realism, as it implies that physical laws may randomly vary on microscopic time scales. Consequently, any set of quantum mechanical axioms becomes mathematically meaningless.
Age: 90 years (900 19C-years).
What we discover upon correcting the mistake: By studying the spatial geometry of Maxwell and Dirac equations' solutions, we learn that both have harmonic and exponential type solutions. Exponential solutions of the Maxwell equation correspond to the tunneling electromagnetic field associated with reflections, e.g. behind a metallic surface, while exponential solutions of the Dirac equation correspond to the quantum tunneling spinor field, e.g. behind a potential wall. No one claims that there should be negative electromagnetic energy associated with reflections, and we prove that the correct energy density calculation indeed yields a positive value. With the help of geometric algebra we offer other geometric analogies of the exponential solutions of the Maxwell and Dirac equations. Once the geometry of these solutions is understood, one realizes that claims of "negative energy spinors" originate from a mathematical misuse of the space-time metric. Happily, there is no further need for confused speculation about temporary violation of energy conservation or about an omni-present but undetectable sea of charged electrons in the vacuum. Electrons and positrons may now be described by the same quantum mechanical wavefunction: both have positive energy, and the only remaining difference between the two particle types is the sign of their electromagnetic scalar field.
3.
Background: Experimental techniques for high-energy proton-electron scattering measurements became available in the 1960s. At that time, proton-electron scattering measurements performed at SLAC did not provide yet a conclusive answer about the number of sub-particles comprising a proton. With the development of experimental capabilities, proton-electron scattering experiments were performed over a gradually widening energy range, which in principle, gave us experimental knowledge with ever increasing accuracy of the proton's internal structure.
Mistaken assumption: Based on theoretical reasoning, most theoretical physicists assumed by the mid-1970s that the proton comprises three sub-particles. This assumption was not quite compatible with the experimental data collected at SLAC, but theorists bridged the gap between their theory and experiment by assuming the three sub-particles are swimming in a "sea of virtual quarks" inside the proton. Such assumption might strike the reader as being particularly extraordinary, but one must remember that its proponents considered it not to be much different from the above-discussed "Dirac-sea of electrons" model, which was already in all standard textbooks. Over the ensuing decades, textbooks started to refer to all these assumptions as "knowledge" about the three sub-particle structure of the proton. Experimentally, it became possible only in the early 2000s to unambiguously count the proton's sub-particles from proton-electron scattering measurements. The corresponding experimental data was collected from the SLAC, JLAB, and HERA facilities. Unexpectedly, highly trained scientists started making elementary data processing mistakes by mixing incompatible data, and published their conclusions in high-impact journals without any peer-reviewer pointing out their basic errors. Not too surprisingly, these published reports reaffirmed the already "known" three sub-particle structure of the proton. As far as we know, the only mathematically correct analysis of these experimental data was published by William Stubbs [4]. We present his results in our book, along with an explanation of the data processing mistakes that one finds in high-impact publications.
Age: 15 years (150 19C-years).
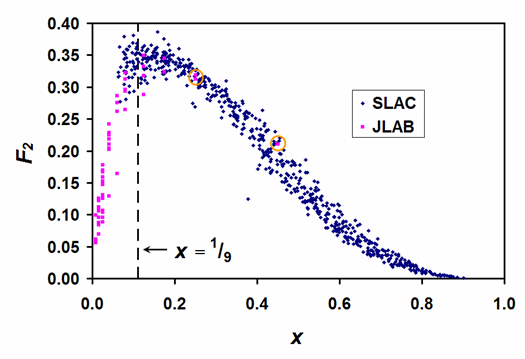
[Above: a figure of the F2 structure function measured by SLAC and JLAB.]
What we discover upon correcting the mistake: Upon carefully combining the sub-particle momentum distribution function from multiple experiments, and refraining from making any unnecessary assumptions, its peak reveals the number of sub-particles in a proton. For X number of sub-particles, the peak distribution is at 1/X. This peak indicates that the proton is comprised of 8 to 10 sub-particles, and there is no need to hypothesize about any "sea of virtual particles". While at the current resolution of scattering data it is still uncertain whether there are 8, 9, or 10 sub-particles, it is no longer uncertain that this number is larger than 3. Investigating these protonic sub-particles opens up a new frontier of particle physics.
[TD note: I disagree with the above narrative, as it is too simplistic. First of all the proton, as any other hadron, is made up of particles of very different properties - quarks and gluons - and counting heads does not tell the story well. Second, for each particle species there is nowadays a very well studied description of the PDF of their momentum fraction; so again, talking about the number of constituents is silly, and only maybe talking about the expectation value of the number of constituents above a given threshold or in a given interval of x can make some sense. Third, of course the number is not fixed and depends on the energy scale at which the proton is probed, as the probability density function of the momentum fraction carried by constituents evolves with Q-squared. Overall, I think the description of static properties by the three-quark picture, and of dynamic properties using the PDF, are complementary and useful.]
4.
Background: By the 1930s, experimenters could measure the electron's magnetic moment at a rather high accuracy. These measurements revealed a slightly larger magnetic moment than what was expected from Dirac theory.
Mistaken assumption: The first phenomenological anomalous magnetic moment formula was published by Julian Schwinger, who recognized that the anomalous part is given by the α/2π expression, where α is the fine structure constant. However, Schwinger claimed to have a theoretical calculation, not just a phenomenological formula. But Schwinger's calculation was based on a point-particle model, which assumes that the magnetic moment of Dirac theory is an inherent property of the infinitesimal point-particle. In the book we show this assumption to be incorrect, and calculate the magnetic moment as a purely electromagnetic phenomenon. Moreover, experts who claim to understand Schwinger's calculation are debating whether his calculation implies a temporary violation of momentum conservation. Most current textbooks go with the interpretation of a temporary momentum conservation violation, which according to Noether's theorem implies that physical laws randomly fluctuate at short distances. As mentioned above, any set of quantum mechanical axioms becomes mathematically meaningless after such speculations. Nevertheless, Schwinger's formula was taken to be more than phenomenological, as physicists already became comfortable with the idea of temporary energy conservation violation, due to the assumption of negative energy Dirac spinors. Soon, Feynman suggested that a more accurate result can be obtained by calculating higher order terms of α. A calculation based on Feynman's method fills 50 pages. One might wonder how it is possible to determine whether such calculation has any predictive power? One may check whether the calculation yields the correct result for various particle types. However, although the coefficients of Feynman's formula yield the correct electron magnetic moment, the formula fails badly for the proton. This was not considered to be a problem, because the proton and electron were thought to belong to unrelated particle families, and so it was assumed that there is a need to apply so-called "hadronic corrections" for the proton case. In other words, it was assumed to be impossible to have a universal anomalous magnetic moment formula for all particle types. By this point, hopefully, the reader sees how all the speculative assumptions are inter-related in a harmful way.
Age: 70 years (700 19C-years).
What we discover upon correcting the mistake: The solution of Maxwell's equation shows that the anomalous magnetic moments of the electron, muon, proton, and neutron can all be calculated from a universal formula. We derive this simple formula from relativistic principles, which reveals that the real control parameter is not α but the charge radius and Zitterbewegung radius parameters. There is no more need to make different calculations for each particle type, no need for 50 pages of calculations, and no need to debate whether physical laws randomly fluctuate at short distances. Based on this, we predicted in the first edition the outcome of the so-called "proton charge radius puzzle": the correct proton charge radius is in fact given by the muonic hydrogen measurements. This prediction appears to be confirmed by a recent proton charge radius measurement [2], which was not yet available at the time of publication. Our results uncover a universal internal geometry among particles which were previously considered to be unrelated, and demonstrate that particles are certainly not abstract points in a wavefunction.
5.
Background: Since the early days of quantum mechanics, it has been recognized that no more than two electrons may occupy any given atomic orbital. For covalent molecular orbitals the same pairwise occupancy was observed. This pairwise rule became known as the Pauli exclusion principle and is at the heart to understanding chemistry. Without this exclusion principle, all electrons would fall into the same ground state orbital.
Mistaken assumption: Pauli was keen to derive the exclusion principle named after him, so that it would not be a new axiom. The derivation worked out by Pauli involved a new principle, which has become known as "micro-causality". In the words of Pauli this principle states that "all physical quantities at finite distances exterior to the light cone ... are commutable" [5]. What Pauli failed to note was that this principle as formulated does not apply to entangled particle states. Entangled particles violate micro-causality by definition and for this reason, within the context of the Einstein-Podolski-Rosen (EPR) paradox, Einstein referred to spooky action at a distance. Regarding the current status of micro-causality principle, it is still debated whether micro-causality is an axiom or a consequence of relativity, and a recent systematic review of pro and con arguments suggests that micro-causality is still in axiom status [6].
Age: 70 years (700 19C-years).
What we discover upon correcting the mistake: We first prove that isotropically spin correlated states can only occur in pairs. In chemistry such states are referred to as "singlet" states, and we show that singlet states are isotropically entangled particle pair states. This essentially means that indistinguishable particle pairs are either entangled as singlets or are statistically independent of each other. From this it mathematically follows that a system of n-indistinguishable particles that contains singlet states must obey Fermi-Dirac statistics, while if there are no singlet states then they will obey Bose-Einstein statistics. Boltzmann statistics follows by relaxing the indistinguishability condition [3]. In contrast to the generally assumed classification of statistics according to half-integer versus integer spin values, we find that spin value has no essential role to play. How can our theorem be experimentally distinguished from Pauli's axiom? Firstly, entangled electron states can be experimentally studied in a wide variety of physical systems, while Pauli's axiom of anti-symmetric wavefunctions is not experimentally observable, as far as we know. Secondly, when two electrons are indistinguishable in the same quantum mechanical state, a break-up of this state causes both electrons to transition pairwise out of this state. Chemists routinely observe this phenomenon for both atomic and molecular orbitals. Regarding atomic orbitals, alkali-earth metals for example are well-known to oxidize directly to +2 valence state, implying a pairwise departure of their outer electrons. Regarding molecular orbitals, the outer electrons of oxygen molecule are known to be in either triplet state (in different orbitals) or singlet state (in the same orbital). In the triplet state the electrons react individually, while in the singlet state they react pairwise. When chemists want to simultaneously bind two oxygens to another molecule, they start by inducing a singlet state of O2 outer electrons. In contrast, there is nothing in Pauli's theory which implies that electrons in the same orbital would be pairwise transitioning. In summary, after 70 years of misunderstandings about the process behind electron statistics and chemical binding rules, we may have a chance to understand the physics of tangible matter. Our theorem is very general, and applies to all particles in isotropically entangled state, for example also to halo nuclei which break up through a pairwise emission of the two halo nucleons.
Altogether the above listed realizations provide a new perspective for the advancement of physics. Since the publication of the first edition, we have received some feedback, both encouraging and discouraging. The more one reflects on the foundations, the more one understands the obstacles that stand in the way of progress. We hope readers will appreciate our quest for truth. Correcting mistakes is by no way disrespectful of the scientists who worked on the involved problems.
Guided by the above insights, we endeavor to develop a realistic electron model. We emphasize that we seek analytic solutions of Maxwell and Dirac equations, without having to make any further assumptions or axioms about particle properties. Our book suggests that less is better and that we can have a more unified understanding of the physical world based on a few fundamental laws. As years go by, the need for a critical discussion on physicists' methods becomes ever more clear. To quote from Lost in Math by S. Hossenfelder [7]:
"It is already clear that the old rules for theory development have run their course. Five hundred theories to explain a signal that wasn't and 193 models for the early universe are more than enough evidence that current quality standards are no longer useful to assess our theories."
The principle of Occam's razor is as valid today as it was in his time, and applying it feels like a breath of fresh air.
References
[1] G. Rousseaux, "The gauge non-invariance of Classical Electromagnetism", arXiv:physics/0506203v1.
[2] W. Xiong et al., "A small proton charge radius from an electron-proton scattering experiment", Nature, Volume 575.7781 (2019).
[3] P. O'Hara, "Rotational Invariance and the Spin-Statistics Theorem", Foundations of Physics, Volume 33.9 (2003).
[4] W. L. Stubbs, "The Nucleus of Atoms: One Interpretation" (2018).
[5] W. Pauli, The Connection Between Spin and Statistics", Phys. Rev (1940), p 716.
[6] J. Wright, "Quantum Field Theory: Motivating the Axiom of Microcausality" (2012).
[7] S. Hossenfelder, "Lost in Math", Basic Books (2018), pp. 235-236.




Comments