The mechanism by means of which a neutron transmutes into a proton has been studied for decades before the neutron was officially discovered (by Chadwick, in 1932). That is because beta decay is at the heart of radioactive processes: nuclei of elements rich with neutrons can turn into others by turning one of their neutrons into a proton, with the emission of an electron and an antineutrino. The details of that reaction were understood thanks to Fermi and a handful of other visionaries in the thirties, but by then the study of radioactive phenomena had even ceased to be at the focus of physicists.
Neutrons can and do convert into protons both inside nuclei and in free space, thanks to the intercession of the weak interaction. However, the speed of the reaction varies wildly inside nuclei, as the neutron there is not a free particle, and its binding with other nucleons (the common term to identify both neutrons and protons) changes the energy budget of the system. So some nuclei undergo beta decay very quickly, and others do so at tantalizingly small rates.
In vacuum, the neutron has a very well-defined mass, 939 MeV or so. This is about 1 MeV higher than the proton's rest mass, so there's enough extra energy to allow for the creation, along with the proton, of an electron (half a MeV of mass) and an electron antineutrino. While the need to emit an electron is clear (the neutron is electrically neutral and the proton has a charge of +1, so there has to be something negatively charged produced when the neutron turns into a proton), at the beginning the neutrino was not thought necessary, and in fact it was not even known to exist.
But the reaction n --> p + e was not what was going on: the electrons produced in the reaction did not have all the same energy, as one would expect when the decaying neutron is initially at rest. It was Wolfgang Pauli who hypothesized that there could be another particle, neutral and invisible, which carried out the excess energy in a 1->3 reaction.
Beta decay as we know it today
The neutron is nowadays known to be a complex system, composed of quarks and gluons. There are three "valence" quarks that give the neutron its static properties: two down quarks and an up quark. The properties are spin, as the combination of the three s=1/2 quarks gives a s=1/2 fermion in the case of the neutron; mass, which is the combination of the intrinsic mass of the components and their dynamical properties; colour, which is neutral as the three coloured quarks combine to give a colour singlet configuration; and electric charge, which comes from the -1/3 charge of the two down quarks and the +2/3 charge of the up quark).
As I already explained, the neutron can decay into a proton, an electron, and an electron antineutrino by the weak interaction. The mechanism is the turning of a down quark in the neutron into an up quark, something that is possible if the down quark emits a negatively charged W boson. "Wait a minute", somebody will say - the W boson weighs 80.39 GeV: how on Earth can this take place, if the down quark only weights a tiny fraction of that?".
The objection would be correct if the emitted W boson were a real final-state particle in the reaction. But the W is "virtual" here: it exists for a time so short that the energy budget does not get affected by its sudden appearance and disappearance. It is as if somebody stole a trillion dollars from the bank, and then put the sum back in place before any accountant could realize that the balance does not make sense.
The W boson in fact turns into an electron and electron antineutrino in a mindbogglingly small time. But the price paid by the reaction for having summoned such a highly virtual W boson is its slowness. The W boson likes to be on-mass-shell: you can rather easily materialize a W boson if you invest 80.4 GeV or more of energy in your reaction, but if you ask the W to content itself with a smaller mass you will make a deal much less often. The poor down quark, having a single MeV or so of energy to invest, has to wait an eternity to pull it off: 15 minutes are a mindbogglingly long time for a quark!
Physicists know the reaction inside out, and in fact they have taken it as the prototype on which to build the theory of weak interactions. In a Feynman diagram where time flows from bottom up and one dimension of space is shown on the horizontal axis, particles are shown as lines and you get to see the movie of beta decay taking place at the quark level. (Courtesy wikipedia)
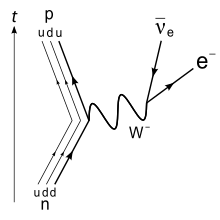
The puzzle with the lifetime
All of the above is history and very, very well known and understood physics. From the understanding of beta decay came a wealth of discoveries in the forties and fifties of the XX century, and particle physics became a thing. But one thing kept physicists struggling: measuring the lifetime of the neutron was a difficult task, and the precision on that important number proceeded slowly. You may check that in the graph below, which also shows something quite interesting.
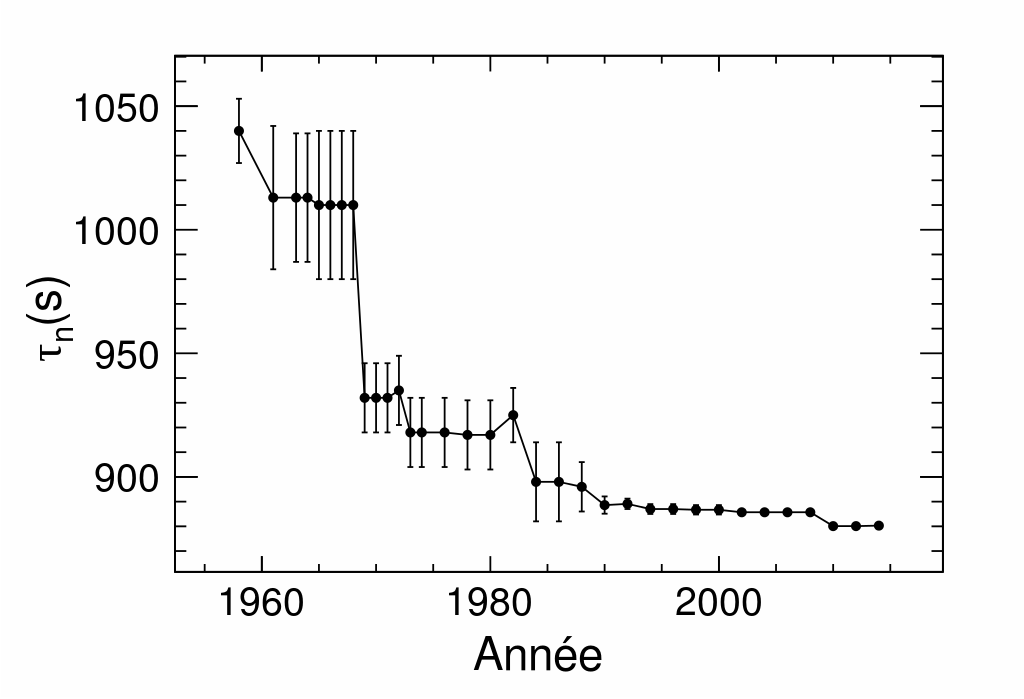
The agreed-upon value of the neutron lifetime, in seconds, is plotted as a function of the year above. As you can see, the value decreased with time quite dramatically, likely due to the combined effec of unknown systematic uncertainties and cognitive biases affecting every new measurement.
Nowadays the neutron's lifetime is estimated by the particle data group at 880.2+-1.0 seconds by combining the result of measurements that don't seem to go along very well with each other. There is nothing intrinsically wrong with this, and in fact the PDG has a habit of critically assessing the uncertainty bar of each determination of any physical quantity they extract an average of. When they accept a measurement to be included in their average, they cook up a "scale factor" to blow up the total uncertainty of their result, accounting for the unsatisfactory level of agreement of the inputs, as measured by the global chisquare of the fit. The details of this statistical procedure, which is arbitrary but is the result of a lot of thinking and debate, are duly reported in any edition of the "Reviews of Particle Properties", the bible of particle physicists containing ALL the data on particle measurements.

Above, you can see the various inputs in the PDG fit to the neutron lifetime. The curve shows the probability density function extracted from the measurements that were combined.
In the case of the neutron lifetime, the scale factor is not enormous but significant - it is equal to 1.9. The figure also reports the confidence level of the combination, 0.0027 - a number which corresponds roughly to a 3-sigma discrepancy between the observed data and the hypothesis that they measure the same physical quantity, if the uncertainty bars are hypothesized to be correct. Is this a signal that the quantities being averaged should not, in fact, be averaged together ? This is a valid question, and it is at the heart of the work published last week.
What if... ?
The authors of the new study make it very clear from the outset what their assumptions are. They reason that the neutron lifetime can be measured in two different ways: by storing neutrons and counting how many survive in a given time, and by studying the observed decays n->pev from a beam. Since the two measurements give conflicting results - the former yields 879.6+-0.6 s, the latter 888+-2 s, a 4 sigma discrepancy - they argue thus:
The discrepancy between the two results is 4.0σ. This suggests that either one of the measurement methods suffers from an uncontrolled systematic error, or there is a theoretical reason why the two methods give different results. In this Letter,we focus on the latter possibility.We assume that the discrepancy between the neutron lifetime measurements arises from an incomplete theoretical description of neutron decay, and we investigate how the standard model (SM) can be extended to account for the anomaly.
I am happy about this: the article investigates a part of the universe of possibilities, and makes it clear that it does not speculates about the other part. The authors use the assumption that neutrons can decay via an unobserved decay channel to explain the 4 sigma difference in the above results, and propose three reactions that are not ruled out by other measurements. In particular, nobody measured photons in the MeV region from neutrons without putting them in coicindence with the appearance of an electron signal. Also, whenever one thinks of alternative neutron decay modes, one must be capable to offer a model which does not include any possibility for proton decay - as the proton is measured to be absolutely stable, its lifetime being longer than 10^34 seconds or so.
There are three possibilities that are considered in the article, and they all involve "dark sector" particles, that are neutral (otherwise we'd have seen them!) and produced in neutron decay transitions involving emissions of photons or electron-positron pairs. The possibility to kill two birds with one stone (i.e., explaining the anomaly in neutron lifetime away AND offering a candidate for the dark matter in the universe) is very appealing, so if you are a researcher working in dark matter searches or if you are a nuclear physicist you should definitely read the article.
Also of interest is that at least one of the possibilities put forth as an explanation of the anomaly is fairly easy to test experimentally, as the decay shown in the picture below (which was taken from the article) should yield "monochromatic" photons, ones i.e. with the same energy, corresponding to the difference between the mass of the neutron and the produced dark matter particle. So if you have a bottle of neutrons in your garage and you can scavenge a photon detector good enough to measure MeV-energy deposits, please go and try to see what happens, then let us know. We will be interested to hear your results.
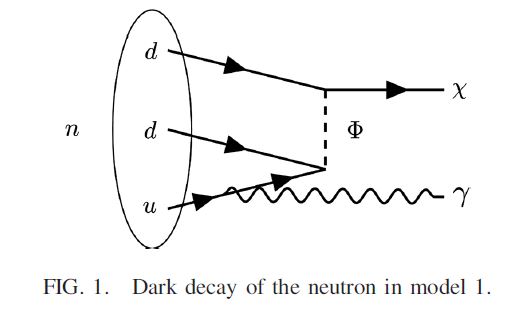
If you ask me what I believe about the above speculation, though, be prepared to a sobering answer. A four-sigma difference between two kinds of difficult measurements of a physical quantity, each affected by different sources of systematic uncertainty, hard to assess and potentially unknown, are very, very poor evidence of anything anomalous going on, leave alone their being insufficient motivation for hypothesizing the existence of not one, but two different new particles, miracolously unseen in other subatomic reaction we ever studied (the phi and chi labeled lines in the graph above).
I can offer a wager of $1000 that no conclusive proof of neutrons decaying into dark matter particles will be obtained within 5 years from now. Wanna bet ?

If you want to bet, just message me and leave the rest of this post alone. Otherwise, you may be interested to know just why I am willing to wager half a month of salary this way.
First of all, the evidence is indeed weak that anything weird be going on. We have measured many parameters of the standard model, and things work quite well overall, but you cannot expect any single measurement to return a value within one sigma from its expectation.
Second, the "four sigma" result stems from accepting that experimental uncertainties have Gaussian tails. But reality is quite different! The probability density of obtaining a measurement x+-dx when the true value is x* is NOT a Gaussian. We like to think it is, because it makes our life easier, but it's a delusion. We say "oh, but the total uncertainty on x is coming from the sum of many small effects, and the central limit theorem guarantees that these will have a Gaussian pdf", but we neglect to acknowledge that more often than not the total uncertainty of our measurements is dominated by a single large source, often uncontrolled and NOT Gaussian in shape. If you are interested about having a discussion on this topic feel free to let me know - I have given over 20 seminars and colloquia on this matter in the past two years.
Third, just **look** at the data presented in the first graph above. Do those uncertainty bar make sense ? They show that there was a considerable cognitive bias at work, when the experimental groups measured the neutron lifetime. They were biased by the knowledge of previous results. This to me says that in this business preconceptions play a large role, as opposed to careful assessment of systematics known and unknown. Mind you, I am not saying those results are wrong or sloppy. On the contrary, I am saying that they are difficult, and that there is a large room for unknown effects to play a role.
----
Tommaso Dorigo is an experimental particle physicist who works for the INFN at the University of Padova, and collaborates with the CMS experiment at the CERN LHC. He coordinates the European network AMVA4NewPhysics as well as research in accelerator-based physics for INFN-Padova, and is an editor of the journal Reviews in Physics. In 2016 Dorigo published the book “Anomaly! Collider physics and the quest for new phenomena at Fermilab”. You can get a copy of the book on Amazon.






Comments