Take the anomalous magnetic moment of the muon. There has been a long-standing mystery about its value, as increasingly precise experimental measurements and theoretical calculations differed by 3, then 4, then five standard deviations. If you allow for new physics processes to play in the phenomenology of muon spin precession, you can indeed get the observable value of that quantity to differ from standard model predictions: hence the interest in the muon's "anomalous anomaly" has remained very high for decades - perhaps (and sadly) the only remaining measurement still at odds with our understanding of subnuclear physics.
Finally, a few days ago an important milestone has been reached, with a bold statement of a group of theoretical physicists that includes all the biggest experts of this special topic. Five years after a white paper where they had assessed the situation, they re-examined critically the vast amount of information provided by theoretical calculations, experimental measurements, indirect experimental evidence, and computer simulations, and finally came up with the same conclusion the rest of us had already reached - but this time with the authoritativeness necessary to put a tombstone on the mystery. In a nutshell, there is no anomaly to speak of anymore. The Standard Model is once again defeating all attempts at bringing it down.
For those who want to know what I am talking about...
To understand what I am talking about in this post, we need to unpack what physicists call "anomalous magnetic moment of the muon". Let us start from the correct place - the end of it. What is a muon?
The muon is an elementary particle that cannot be found in ordinary matter. It can be produced in energetic subnuclear reactions - either by particle collisions or from the decay of other particles. Discovered at the end of the 1930ies and soon understood to be a sort of heavy replica of the electron, the muon carries one unit of electric charge and it "spins" around some axis - admittedly something hard to picture if you consider the muon to be pointlike, as we do.
Because it is a spinning electric charge, the muon possesses a magnetic moment, exactly as the electron does: it behaves like a tiny magnet. Now, if you take classical electrodynamics and you try to compute the magnetic moment that the muon should have, given its mass and spin and charge, you come up with a number which is exactly equal to 2, in some suitable units which we can ignore for the sake of this simplified discussion. Yet, the true magnetic moment of the muon is not exactly two, but slightly off of it.
The difference, called "anomaly", is due to the fact that some properties of quantum physics do not work exactly in the same way as their macroscopic counterparts. For the magnetic moment of spin-1/2 particles of unit charge, classical electrodynamics predicts 2, but quantum electrodynamics produces an anomaly - a small variation, which depends on the particle in question.
In the fifties of the past century Richard Feynman and Julian Schwinger broke a lot of ground when they demonstrated how the rules of quantum mechanics allowed an extremely precise measurement of the anomalous magnetic moment of the electron. The verification of their calculation down to 12 decimal digits stands as one of humanity's most giant steps in the understanding of physical reality, and was the motivation of one of the most deserved Nobel prizes in Physics.
And what about the muon then? Being 200 times heavier, but otherwise a very similar particle to the electron, the muon also has an anomaly in its magnetic moment. The larger mass of the muon may however bring a much higher sensitivity of that quantity to phenomena triggered by new forces of nature that preferentially affect heavier particles. Hence the muon anomaly carries direct information on the existence of new physics beyond the standard mode, that might instead leave the electron anomaly unaffected.
Experimental determinations
Measuring the muon anomaly is much harder, however. For one thing, you need to produce muons - those things do not come for free as electrons do. The way to get a beam of muons is to direct an energetic beam of protons onto a target, sort out light downstream hadrons (pions and kaons) emerging from the resulting collisions, and let them decay in flight: both charged pions and charged kaons can decay to a muon and a neutrino. Then you need to focus the resulting muons into a narrow beam, which you inject into a circular ring where they can be made to orbit, and where their magnetic moment can "precess" in the magnetic field.
Muons however are unstable particles: they decay in 2.2 microseconds, on average. But if you accelerate them to speeds close to the speed of light, time flows more slowly for them - a result of special relativity - so in the laboratory you may get to study them for tens or even hundreds of microseconds. During that time their magnetic moment can precess many times, so that you can measure its direction you get to measure its value.
... But how do you pull that last bit off?
That is in truth the easy part! When the muon decays, it produces an electron whose direction of motion relative to the muon is correlated with the direction of the muon spin. By detecting the number of decays in a given direction as a function of time, you get to access the precession frequency, and voila! The measurement is done!
The Fermilab g-2 collaboration has been performing the latest measurement of this quantity, after importing from Brookhaven the apparatus used in earlier studies. And they just released their final result, based on the collection of a very large sample of muon decays. This last result has a much better accuracy than earlier determinations, as the graph below shows...
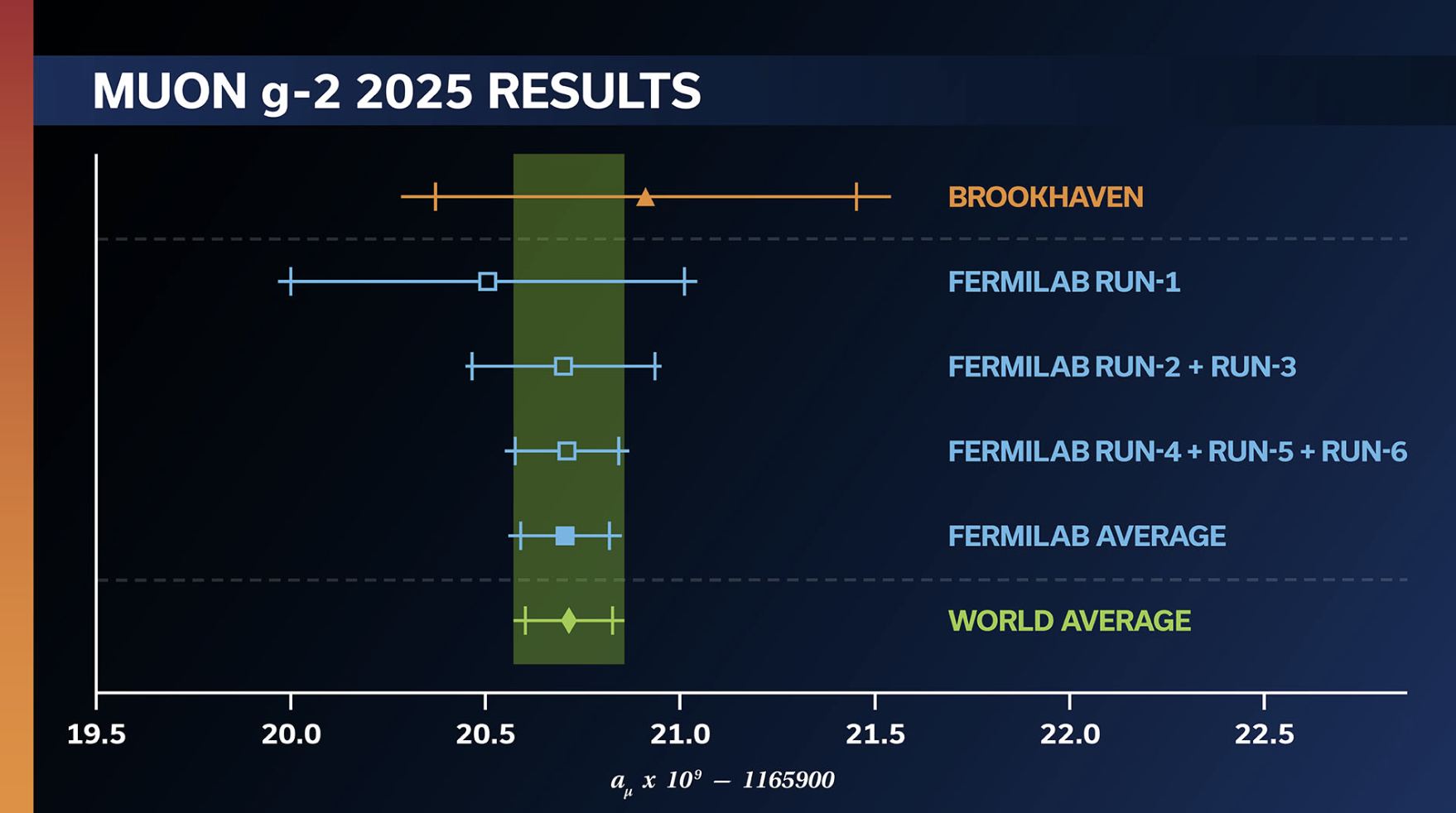
[Above: increasingly precise determinations of the muon anomalous magnetic moment, from the early Brookhaven result (top) to the latest-greatest Fermilab result.]
A success story, indeed, and a wonderfully precise assessment of the muon anomaly. But this comes only a few days after the theoretical paper wasted all the punch off of it. Let me explain what happened there.
Unconventionally sober theorists
Usually, theoretical physicists will be keen to evidence discrepancies between experimental measurement and calculated predictions for particle physics processes. During the past century this modus operandi produced a few groundbreaking advances in our understanding of the subnuclear world: a difference between a measurement and theoretical calculations of an observable quantity calls for an explanation, and the Ockham-approved explanation involves new phenomena that are later discovered. By Ockham-approved I mean that the simplest explanation still involves calling for the existence of new entities. The 13th century philosopher correctly understood that "entia non sunt multiplicand a praeter necessitatem" - you should not invent exotic new entities in your investigation of the world; but if you need to, better to pick the explanations that involve the fewest of these.
Perhaps the most notable example of this was the discovery of the charm quark, which had been hypothesized to exist because it would explain the extremely small, but non-zero, branching ratio of neutral kaons. This was the intuition of Glashow, Iliopoulos and Maiani, and their "GIM mechanism". The GIM mechanism involves a quantum loop of quarks to allow for the disintegration of neutral kaons into muon pairs, and only if you include a heavy quark in this loop can you get the prediction to match observations.
So the step the g-2 experts have taken in their latest work is unconventional, because rather than rejoicing at the now established discrepancy between the experimental value of the muon anomalous magnetic moment and the Standard Model predictions, they accepted the writing on the wall: those predictions are flawed by being too reliant on some experimental input which stands on too shaky ground; a new methodology to bypass that experimental input and rely on powerful computer simulations using Lattice QCD instead produces a perfect agreement with the Fermilab result.
The paradigm shift is really remarkable, but in order to appreciate it I need to explain what is the culprit. When theorists compute the muon anomaly, they rely on the same technique that Feynman and Schwinger used 70 years ago: 1) sum up together all the contributions to the magnetic moment of the muon coming from quantum diagrams with an entering muon and an exiting muon and photon (what is called a quantum amplitude, a complex number that summarizes the strength of that interaction), 2) take the square of the modulus of that amplitude, and obtain an intensity that can then 3) be converted in the wanted magnetic moment. However, some of the contributions to that amplitude come from quantum loops that involve the exchange of hadrons - particles made of quarks and gluons. And that is a problem in this case, unlike in the case of the GIM mechanism.
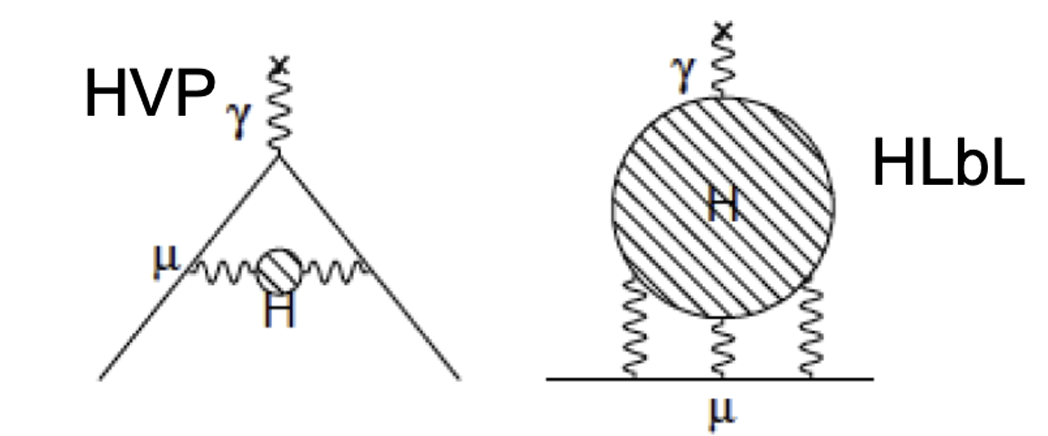
[Above, the two diagrams where hadronic contributions affect the interaction of a muon with a magnetic field: hadronic vacuum polarization, and light-by-light scattering. In both cases the muon is the solid line -making an angle when it emits the primary photon on the left, and emitting three virtual photons on the right.]
Hadrons in quantum loops are not special per se, but to compute the amplitudes of diagrams that include their virtual exchange requires you to use quantum chromodynamics, the theory of strong interactions. Being strong, this interaction features a large number for the "interaction strength" between the involved particles. Now, while the methodology of Feynman and Schwinger, which entails computing the sum of an infinite number of smaller and smaller terms, works well for electromagnetic and weak interactions, where every contribution in the sum is smaller than all previous ones (such that the series converges and you can stop at some point when you get bored), with strong interactions all those quantum contributions do not get smaller as you work out their values. What you have is a non-converging series! Basically this throws a monkey wrench in the whole mechanism, and you are back to square one. Hadronic contributions to the muon anomaly cause a small correction to the value you compute by only considering electroweak interactions, but the exact size of that correction is not computable.
[And why then could GIM pull that off instead, could the argute reader now ask? Well, for the Harvard trio to estimate the charm quark mass it was only necessary to compute the leading order diagram allowing the rare kaon decay, which involved a single quark exchange (of three different kinds in fact, one of them being the charm; it worked well that the top quark, still not even conceived, did not play a very large role there). In that diagram the interaction these virtual quarks withstand is weak, not strong; if you had to compute a higher-order correction to that diagram, the fact that you have quarks propagating in the quantum loops would force you to then consider strong interactions between them, and you would be in hot waters again; but the GIM prediction did not require that kind of precision. For a precise estimate of the muon anomaly, however, that is unfortunately necessary, as experimental precision is so high it calls for incredibly subtle effects to be sized up!]
Until a couple of decades ago, the only way to assess the value of the QCD correction to the muon anomaly was based on indirect experimental measurements of other subnuclear processes that were affected by the same kind of quantum loops. The reasoning was like that: if an electron and a positron annihilate into a virtual photon, and the latter produces hadrons, the rate of this process must include corrections due to virtual QCD loops where the photon fluctuates for a brief instant into a quark-antiquark pair; and everything else that those two quarks can do while we are not looking a them. So the same processes take place when the muon interacts with a magnetic field (virtual photons are involved again), and thence one could export that part of the amplitude from one process to the other. Unfortunately, there are subtleties that make this plug-and-play kind of methods affected by hard-to-assess systematic uncertainties.
Enter the Lattice, exit new physics
What happened in recent times was that QCD became a calculable theory. Not everybody would agree to this statement, but the fact that the g-2 theorists now say that there is no discrepancy in the muon anomaly goes a long way in that direction. Basically, in lattice QCD you compute the interaction between hadrons by discretizing spacetime, and then taking the limit where the lattice spacing goes to zero. This is easier said than done, because when you compute all the paths that particles may take on a lattice to go from a point to the other, you get explosive combinatorics and computation time becomes nightmarish. But it can be tamed, and supercomputers today can produce incredibly accurate prediction for the mass of bound states of quarks - the many hadrons we have measured so precisely in the past fifty years. That experimental validation proves that we can rely upon the estimate that lattice QCD provides for the QCD contribution to the muon anomaly.
And this brings us to today's situation: the experimental measurement is as precise as it has ever been, and it is well above five standard deviations away from the old-fashioned Standard Model prediction - the one which employed systematics-riddled experimental indirect inputs to assess the size of the QCD corrections. But nobody cares any longer, as the scientific consensus is that that prediction is the problem, because it disagrees with the lattice QCD calculation! The tables have turned, as many colleagues would some time ago have bet one testicle on the fact that lattice QCD was wrong precisely because it did not agree with the old-fashioned data-driven estimate. I hope they did not, as the fertility rate is declining everywhere in today's world.
A striking - and a bit ironic - way to observe the paradigm shift that has taken place is to note how the Fermilab g-2 experiment, who now publishes its final measurement, has entirely stopped arguing about the discrepancy (now non-existent) with the theoretical prediction. That is because there is none any more to speak of! Compare the graph above with the one the g-2 experiment released in 2021, where a lot of focus was given to the SM prediction (of course supported by the previous theoretical consensus, which is labeled "WP2020", the 2020 white paper I mentioned above):
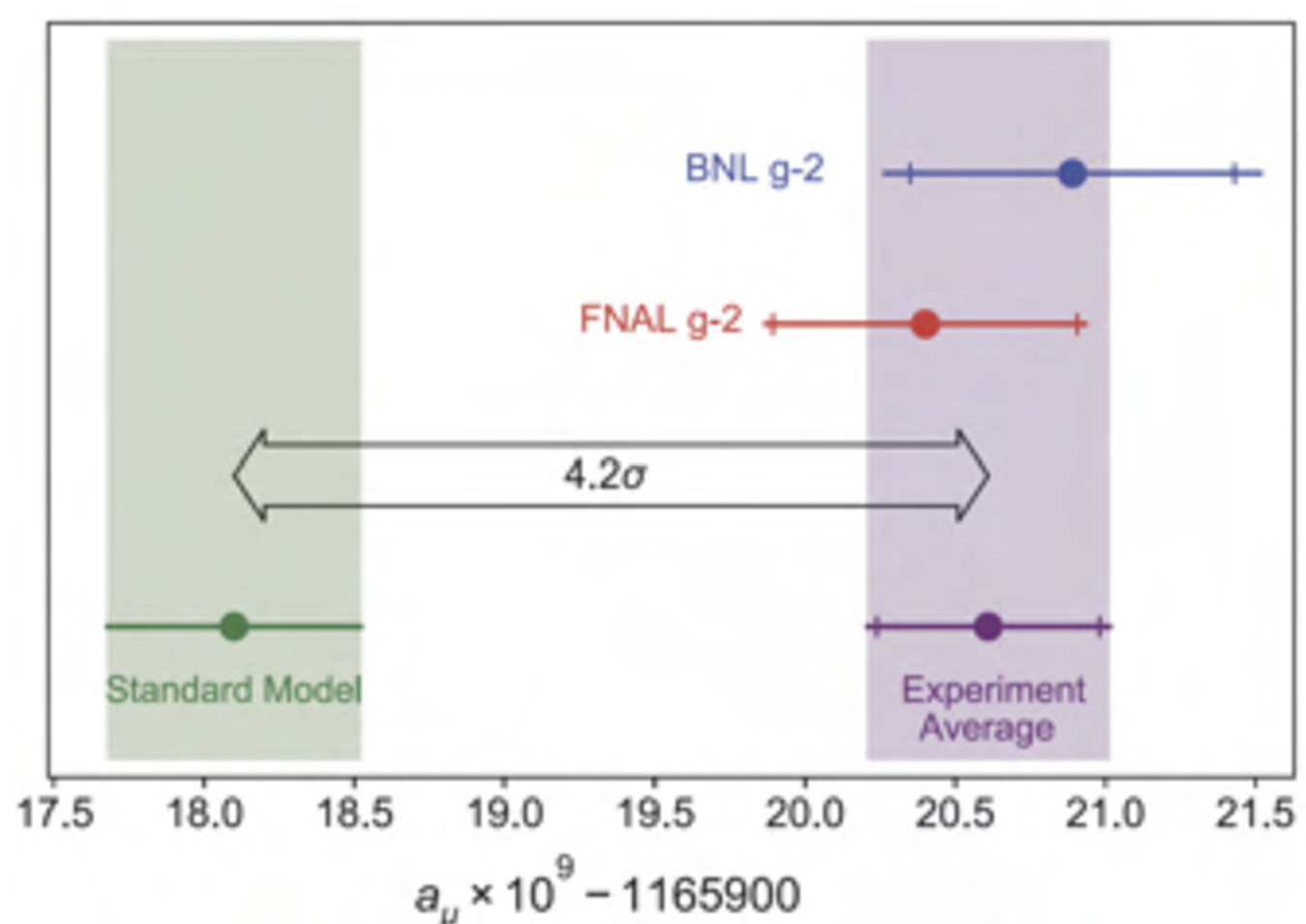
[Above, a summary of the tension between theoretical calculations (left) and the experimental average (right) as of 2021. People used to talk about 4, and then 5-sigma, discrepancy of the muon anomaly back then. Not any longer.]
Also gloomy is the picture emerging from the statement of Lawrence Gibbons, analysis co-coordinator of the result now published by the g-2 experiment. Quoted from the Fermilab press release, here is what he has to say about their new result: "For over a century, g-2 has been teaching us a lot about the nature of nature. It's exciting to add a precise measurement that I think will stand for a long time." I would paraphrase it as follows: "We came to prove new physics, we ended up publishing a uncontroversial result that nobody will ever care to improve upon." But that is precisely how science progresses. It is jut not always Nobel prizes and big headlines.
So, there goes another anomaly. Bottom line? You needn't ask - the Standard Model rules!





Comments