As seen in the article on the hydrogen atom the value of a number numerically equivalent to Planck's reduced constant comes from the equations for the energy of the electron as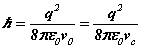 
from the self-field theory (SFT) formulation and can be calculated from the solution of the Bohr radius and the resonant frequency. The known value of Planck’s reduced constant compares with this analytic estimate to an accuracy of 7 significant figures. The known value of this physical constant comes from experiments that have continued till the present starting with Planck's black body experiments in 1900. Planck's constant is obtained by examining the spectrum of a black-body radiator or the kinetic energy of photoelectrons. What we have here with the SFT formulation is the first known analytic expression for Planck's 'constant'.
Planck's 'number' in the SFT formulation is actually a variable of motion that can be obtained as an energy per cycle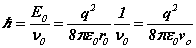
. For the electron, 
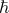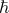(or electron) depends on the elementary unit of charge, the dielectric permittivity of the medium under consideration and finally the electron's velocity. In other words this 'number' does NOT just depend on the 'constants of nature' but is a variable of motion. Hence in the same way that quantum theory applies to many situation as well as atomic physics, there appears to be a particular 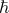for many different situations.
Planck's reduced number is thus found within the SFT formulation; it just stands out like a lighthouse beacon. MAPLE was used to solve SFT's Maxwell-Lorentz equations analytically. 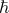has become a staple of quantum theory. As we know, it is the heuristic basis of ALL quantum theories. The fact that it arises not just as a 'constant of nature' but as a variable of motion for the electron reveals the fundamental nature of SFT and how it fits into the foundations of quantum theory.
So what does this mean for the quantum formulations that are based on 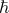? Quite a lot that's relevant to the past, the present and the future. We shall take this slowly because it is important to appreciate the implications. So let's just map out what it means for the earliest days of quantum theory in this article and leave any other implications for further articles in this series on SFT.
Figure 1 The Early Discoverers of Quantum Theory: Planck, Einstein, Bohr and Heisenberg
(Credits http://www-history.mcs.st-and.ac.uk/PictDisplay/Planck.html
http://www.losmuchachosdelbarrio.com
http://theenergylibrary.com/node/10852
http://www.notablebiographies.com/He-Ho/Heisenberg-Werner.html)
While Quantum Theory hardly needs validation, SFT does indeed provide the first actual theoretical validation of this form of mathematical physics that has been at the forefront of 20th century science and technology. Till now quantum theory has been a heuristic formulation. Now, it is a method based on mathematical theory. While this may seem somewhat ludicrous to some practitioners we need only read our quantum mechanics primers to realize that Planck's constant was applied in heuristic fashion and was not incorporated in quantum theory as an intrinsic constant due to the formulation.
Euler, Cauchy, Lagrange, and Fourier all developed the theory of eigenvalue solutions to differential equations. These problems were a variety of wave equations that had been known since Isaac Newton first developed the calculus methods and discovered differential equations. Hilbert at the start of the 20th century studied the eigenvalues of integral equations operators for the case of infinite matrices. Being German he used the term 'eigenvalue' instead of the English term "proper value" found in early texts on quantum mechanics such as "Atomic Structure" by E. U. Condon and H. Odabasi Cambridge Univ Press, 1980. It was only natural that since the eigenvalue method could handle the problem of infinite matrices for wave problems that two particular 'postulates' were employed in quantum mechanics. (A postulate is an assumption that has no proof.) One of these postulates relates to wave equations and the other relates to eigenvalue problems.
The central idea of quantum mechanics is that the variables can be quantized by formulating the physics of the atom as an eigenvalue problem. Thus we write in general terms
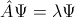where the eigenvalues are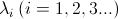 
In 1900 Planck assumed that radiation was being emitted as discrete particles called photons rather than a continuous stream of energy. The energy
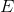of the photon is
related to frequenc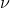y 
by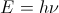 
. The quantity h, Planck
constant, has been assumed to be a universal constant with the approximate value of 6.626 X 10-34
J s. This constant was the eigenvalue inserted into the general equation. Hence we see that quantum mechanics was indeed a heuristic method where Planck's constant came from the black body studies and then Einstein's photoelectric experiments in 1905. Bohr's theory was introduced in 1913 while Heisenberg in 1927 introduced the matrix method and uncertainty into the formulation. Heisenberg's infinite matrices for position and
momentum did not commute as in classical physics:![[X,P] = X P - P X = i \hbar](http://upload.wikimedia.org/wikipedia/en/math/0/3/4/0342ffe593429f253ff09a217ad29be5.png)
Before these postulates were established in the 1920's Planck in 1899 considered there were 'natural' constants including Planck's reduced constant.
...ihre Bedeutung für alle Zeiten und für alle, auch außerirdische und außermenschliche Kulturen notwendig behalten und welche daher als »natürliche Maßeinheiten« bezeichnet werden können... ...These necessarily retain their meaning for all times and for all civilizations, even extraterrestrial and non-human ones, and can therefore be designated as "natural units"... _http://en.wikipedia.org/wiki/Planck_unitsHe investigated a number of similar and related constants that became known as universal constants.
- Newton's Gravitational constant, G;
- Reduced Planck constant, ħ;
- Speed of light in a vacuum, c;
- Coulomb constant,
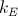
- Boltzmann constant, kB .
"Planck units elegantly simplify particular algebraic expressions appearing in physical law. Originally proposed in 1899 by German physicist Max Planck, these units are also known as natural units because the origin of their definition comes only from properties of nature and not from any human construct." _http://en.wikipedia.org/wiki/Planck_unitsThe universal constants in Planck units are set to one. Thus Planck's reduced constant has been considered from 1899 till the present time to be a constant whose definition comes only from the properties of nature.
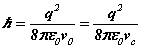(1)The discovery within SFT of a variable of motion given by (1) that is the numerical equivalent of Planck's constant is fundamental to our understanding of both quantum mechanics and the composition of the Universe. It reveals for the first time an analytic expression for what can be termed Planck's variable of motion for the electron.
Like Galileo's discovery that the Sun did not revolve around the Earth, the equation for Planck's variable of the electron inside the atom given by (1), reveals the likelihood that the composition of our local region of the Universe may not be representative of the entire Universe, as Dirac had speculated.
We shall at some stage in the future discuss the use of quantum theory across physics and how Planck's variable of motion reveals why quantum theory does indeed apply across physics.
Heisenberg's uncertainty principle) is used as a way of supplying the missing ordinate, and 
) is used for the same reason.
People have measured if Planck's constant is constant by looking at physical systems that depend on the fine-structure constant alpha which does have Planck's constant. Since the find structure constant does not change going way back in the Universe, I will stick with the experimental data instead of your proposal.
By the standard rules of algebra, nu0 must equal nuc. Changing a subscript should change nothing. I recognize you take the equation seriously, but it does not look informative to me.