Banner
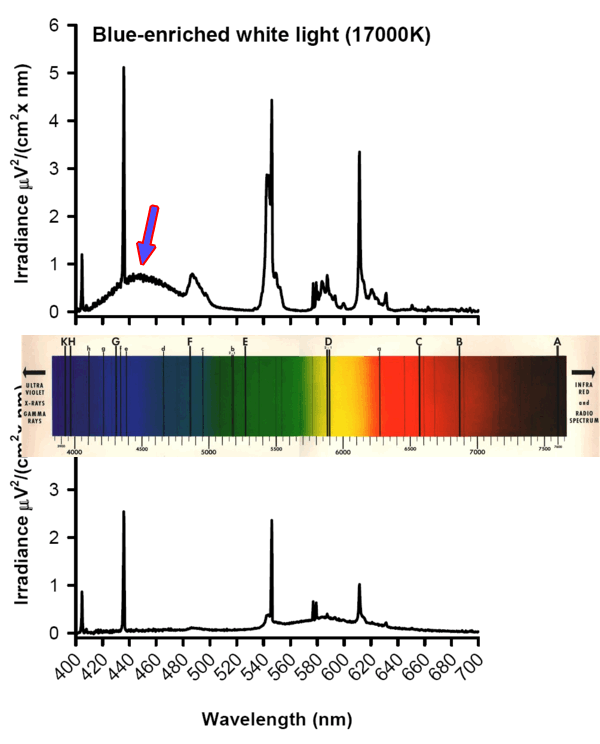
Not So Elementary (the Cosmos, That Is)

Recently there are appeared a paper showing how Physics - Iron–Helium Compounds Form Under...

Carbon — to capture or not to capture

This came up on 2nd November 2024 (give or take a day), a broadcaster objecting to a carbon capture...

The Azolla Event: when is a fern not a fern?

...

Betelgeuse, Gamow, and a Big Red Horse

There has been a lot of talk recently of Betelgeuse possibly going supernova this century or not...

User picture.
picture for Hank Campbellpicture for Helen Barrattpicture for Hontas Farmerpicture for Sascha Vongehrpicture for Patrick Lockerbypicture for Sean Gibbons
Robert H OlleyRSS Feed of this column.

Until recently, I worked in the Polymer Physics Group of the Physics Department at the University of Reading.

I would describe myself as a Polymer Morphologist. I am not an astronaut,

... Read More »

 Blogroll
Go Blue To Clear Those Office Blues!

Go Blue To Clear Those Office Blues!

Nov 03 2008 | comment(s)

Does your office lighting make you feel weary and dreary?  The cure may be at hand!  Recently, Professor Derk-Jan Dijk of the Surrey Sleep Centre has led a team testing out new bulbs with a colour temperature of 17,000 Kelvin and found that they increase alertness as compared with more traditional types of lighting. But this sounds rather alarming.  17,000 Kelvin would be the temperature of a star close to B3 in the main sequence, somewhere between Alkaid and Regulus in properties.  The luminance of these stars is largely in the ultravio
Sex Education and Science Teaching

Sex Education and Science Teaching

Oct 24 2008 | comment(s)

I have been reading a blog entitled (wouldya believe it?)

Catholic bishops back sex education for primary school children.

Now it's not the blog itself, but a couple of the comments have set me a-thinking.  One says:
Sure Start will be made nationwide and ultimately the plans of Ed Balls
is that children are educated from the age of two in such places
because inequalities and values can be established before the age of 5.
Ethnomathematics And History

Ethnomathematics And History

Oct 22 2008 | comment(s)

Ethnomathematics! Doesn’t the very term conjure up visions of politically correct wallahs (and walis) trying to prove, in a postmodern way, that “all cultures are equal”?

True, previous generations of math historians had tended to be unjustifiably Eurocentric, though the really great ones, like the Swiss-American Florian Cajori (1859 - 1930) were certainly not so. But to me there are two great benefits to be gained from the study of the maths of the East.

Firstly, the achievements of China, India and the Middle East give the lie to any postmodern assertion (if that’s not an oxymoron) that mathematics is a culture-dependent thing without any fundamental underlying reality.
44 years of academic life

44 years of academic life

Oct 16 2008 | comment(s)

Not me! I've only clocked up 36 years, with two to go. But I thought that this article is worth reading: 44 Years of Academic Life: So what changed?. It's not even from a science department, but it does sum up the mood of academia in Britain today. Any thoughts from readers on the Continent or in North America?
How inappropriate!

How inappropriate!

Oct 09 2008 | comment(s)

Juno Spacecraft to Study Jupiter, we are informed by space.com. Don't people think before they give names, or choose songs? They select for weddings "I will always love you" by Whitney Houston, which is a song of irreversible parting, and I have even heard of a Church of England vicar choosing John Lennon's "Imagine there's no heaven" for something or other. I live on the eastern side of the Pond, which makes me a European, and the name of our continent is taken from that of Europa in Greek mythology.
CyberStasi

CyberStasi

Oct 06 2008 | comment(s)

Nachrichten aus Großbritannien

Government spies could scan every call, text and email

Ministers are considering a £12 billion plan to monitor the e-mail, telephone and internet browsing records of every person in Britain. This is the heading of an article in today's Daily Telegraph. Two questions: Would it work? (Especially with our government's record of sloppy data handling) How would one escape over the Firewall?