I enjoyed Johannes Koelman's blog, "Velocity: Stuff That Doesn't Add Up."  If you haven't read it, please consider doing so. I will review just the math here. There was a technical point that probably flew over many a reader's head. When discussing the elegance of the Lorentz relativity approach, he mentions a hyperbolic tangent.  Hyperbolic trig functions used to cause me hypertension. With a little math and a few pictures, gone is my fear. Hopefully the reader will feel these strangers are not so strange after reading this blog.

Galileo Velocity Roundup

Galileo gazing at ships proposed a simple cycle of addition law for velocities. There are three players in this cyclic game: a fly (F) in Travis' ship (T), and Stacy (S) staying on the dock. A velocity V_FT=10^-8c means the fly is moving on the ship towards Travis at about 6 knots. Travis is sailing toward Stacy at 20 knots. Stacy is watching the fly. The law is:



What Stacy sees is the sum of both the fly's velocity on the ship, and the ship's velocity towards her. What is key here is the cyclic arrangement of the subscripts, FT:TS:SF. Note: Galileo did not write this expression because he was not aware of the development of algebra developed in the Middle East.

For everyday flies and people, Galileo's velocity law of addition is simple and useful. A problem does occur for things travelling near the speed of light. Galileo did try to measure that speed in his own day, but was a sharp enough an experimentalist to realize light was too fast to measure using human reflexes. Impressive.

Trains, planes, and automobiles never get near the speed of light, nor do flies or people. Only simple particles can be so zippy. Imagine there is a particle T that is travelling at a speed 2/3c compared to a Stationary detector (S).  That particle emits another particle F that goes at half the speed of light relative to T. Add the velocities up to see what is seen at the stationary detector:



This was not a problem until 1905 when Albert Einstein, peering deeply into the Maxwell equations, realized an equation like this:



means that electromagnetic waves must travel at the constant speed c no matter who the inertial observer happens to be (it was not this actual equation that launched his interest in the subject).

Is there a new velocity law that could deal with the upper speed limit? What one needs is a fourth term, one that is the product of the other three:



I had never seen it written this way. Let's solve for one of the terms, say V_SF. Toss the other terms on the other side, do some collecting and rearranging:



This is the form I had seen many times. Check that it works:



This is less than one. It takes much more effort to show this is what Nature does and has been confirmed by experiment, but that is not the purpose of this blog.

The math so far has been simple: addition, multiplication, and fractions. Johannes asks if the elegance seen in the Galilean law has been lost. Here is his description of the situation:

The Lorentzian velocity equation has an additional term compared to the corresponding Galilean equation. This triple velocity product term is negligible compared to the other terms when all relative velocities are small compared to the speed of light. Yet, it still is an extra term. Somehow it seems that Lorentzian/special relativity is less elegant than Galilean relativity.

This is no more than an appearance. An appearance that disappears when one looks deeper into the concepts playing a role in both relativity theories. Galilean relativity places a lot of emphasis on velocities, not so Lorentzian relativity. Einstein's theory that leads to Lorentzian relativity is based on a spacetime description in which velocities are represented as slopes. Would the time and space dimensions behave similarly, velocities relative to an observer would be the tangent of angles with the time-axis relevant to that observer. However, time behaves in a way subtly different from the way spatial dimensions behave, and as a result velocity is measured by the hyperbolic tangent of an angle with the time-axis. This angle is referred to as rapidity. And the point is: these angles (rapidities) do add up to zero. That is to say: a Lorentzian rapidity composition formula would take the shape of three rapidities adding to zero. A Galilean rapidity composition formula, on the other hand, would be ugly. In terms of rapidities, Lorentzian relativity is the most elegant form of relativity.

The two words I highlighted in bold, hyperbolic tangent, may have lost 90% of any remaining audience. The rest of this blog is targeted to those who feel comfortable with standard trig functions - even if you forget which one is opposite over the hypotenuse - but feel at a total loss about hyperbolic functions.

Start with the familiar trig function trio: sine, cosine, and tangent. The three amigos involve games with right triangles inside of a circle, three of the possible ratios between the lengths of sides. The hyperbolic sine and cosine are triangle games with hyperbolas. The equation for a hyperbola is this squared minus that squared equals a constant. This time there is no ratio, only one side or the other. Here is a visual summary of the math:

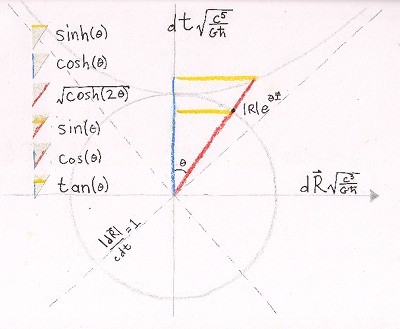
A few notes on my own quirks. I like my math and physics to mingle.  Math plays with pure numbers 99% of the time. By using time and distances that are ratios of Planck units, everything going into the graph is also dimensionless. The circle can be any size and the trig definitions still hold.

The standard trig functions all work with one circle that rules them all. If sine is zero, then cosine is one, and visa versa. Consider all the extremes, where the four triangles "get flat":


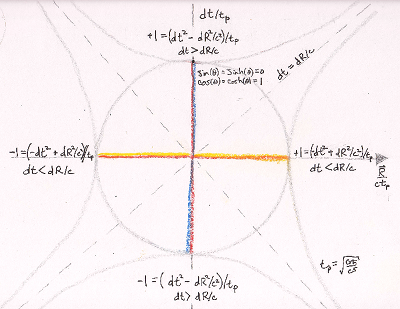
At the top of the circle, there is the one direct connection between the regular and hyperbolic trig functions:



Now we can see a limitation on our calculators. They are all programmed to use the timelike future lightcone curve of the hyperbola. Fortunately, a few appeals to symmetry and the calculator can figure out what goes on for each of the other three curves. Let's create names for three new hyperbolic functions associated with the left (sinh_L, cosh_L), right (sinh_R, cosh_R), and past (sinh_P, cosh_P). The easiest is the past hyperbolics because they get minus signs:



For the right hyperbola, the values of sinh and cosh change places due to a reflection over the t=R/c axis.



A similar thing happens for the left hyperbola. The twist is the unitary one must map to minus one:



Let's take a step back though. Which one is the unitary one? Which one can be zero? Here is where a little fact of special relativity comes in handy:



When the relativistic velocity beta is zero, so is the hyperbolic sine. It is gamma that has a minimal value of one, otherwise it is greater than one, as is the case for the hyperbolic cosine. Sometimes knowing physics helps with the math.

It is this angle theta that is known as the rapidity. If anyone complains about the speed limit imposed by light, point out that there is no limit on the rapidity. Choose whatever number you want, it will work to calculate the velocity. Playing silly number games, I found out a rapidity of 1153 has a relativistic velocity written out to a thousand significant digits that is a wee bit short of unity (it is nothing but 0.999999...). This is where Johannes comment comes from:

By the way: next time you meet folks who believe in tachyonic neutrinos: ask them what rapidities these neutrinos attain...

Animating Hyperbolic Trig Functions

Look, it is on wikipedia, it must be true and complete (created by Sam Derbyshire):

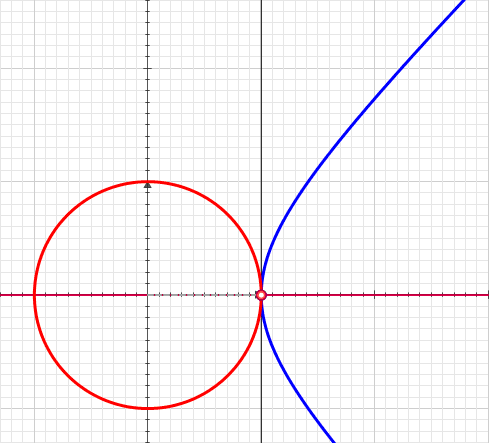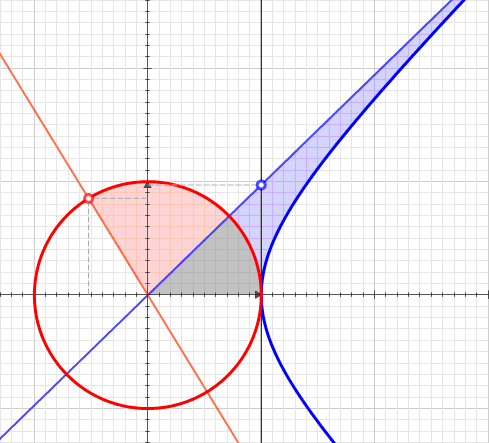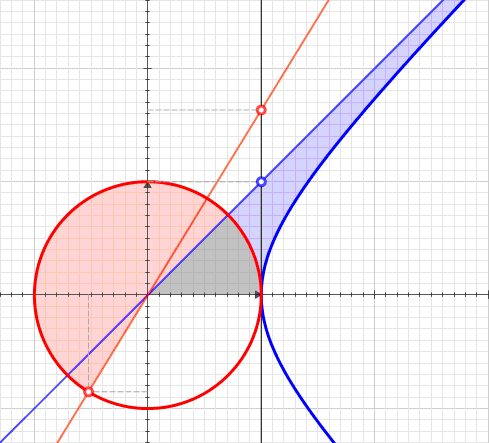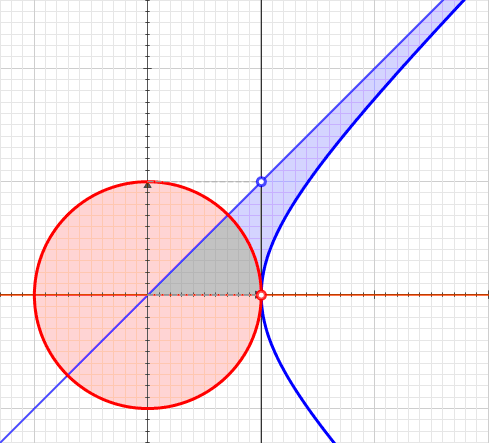
Wikipedia can be a good training in critical reading. One can see that only one hyperbola is used. That is true, but from the point of view of this blog is not complete. Here are what my own software generates for the hyperbolas and the circle:

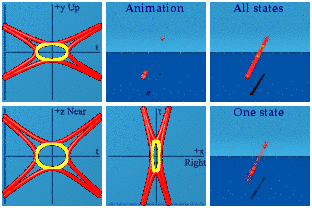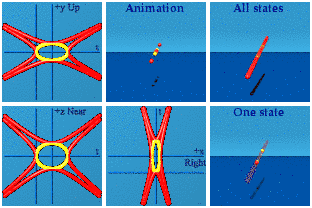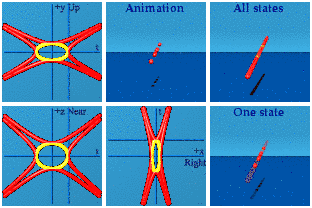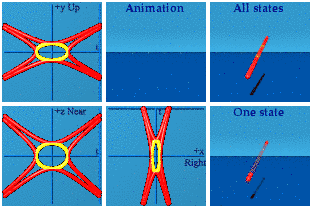
I like that I can see the four red curves on the screen for most of the time. Two are for a timelike separated hyperbola, while the other two are spacelike separated. When the first red ones make contact with the creation events in yellow, two of the reds disappear (those are the spacelike pair). One can see the remaining two reds make fleeting contact with the yellow events. The reds start separating, the yellows move to get closer until they annihilate.

There are two symmetries that are easy to see once you know how to look for them. A time symmetry in an animation means the animation ends in reverse of how it begins. You must use your memory to recall how things started, then play that memory backward. This animation is symmetric in time.

Things that are symmetric in space have pairs of events that move as one would expect in a 3D mirror. Both the yellow and red events come in pairs who do a synchronized swim. This animation is symmetric in space.

I have not put in the work to figure out the trig functions with these animations, sorry. Still, I hope you feel more familiar with the hyperbolic trig functions now.

Doug

Snarky puzzle: Show that addition of rapidities is the same as the velocity addition rule with the triple product. Don't ask me for help, I don't know the answer yet, but it sounds like a well-formed question.

Next Monday/Tuesday: New Toy Model for Q8 (if I can find 1/16" dowels).