The word "retracted" was not used in the title since it is associated with fraud. Editors will retract papers from journals when they determine the data was fictional, not factual. Rescind is being used in the sense of repeal. I am no longer trying to promote the GEM unification proposal because it is wrong.
Rescinding work is not part of the culture of science, although there are counter-examples recently written about here by Robert Cooper http://www.science20.com/profile/robert_cooper http://www.science20.com/caution_pondering_scientist_ahead/scandal_scien.... Work on supersymmetry may someday be ignored, but not rescinded. Data from the LHC continues to cast data-driven doubts on the existence of any supersymmetric particles. The published papers on supersymmetry passed peer review. We lack a device to say nice try, but the data says the body of work is wrong. The only mechanism science culture uses is the "dustbin of history".
Let me be specific in what I am rescinding - the content of a t-shirt which has the field equations and Lagrangian:
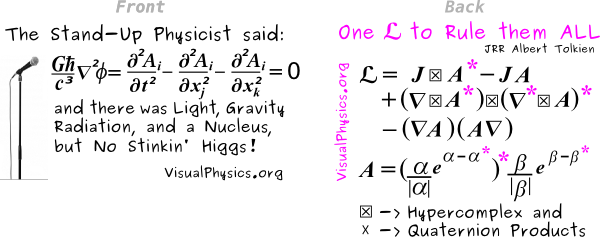
I have made a YouTube video reading of this blog and put a link in many of my other YouTube videos. There will be a talk on this subject at the Fall 2012 APS meeting at Williams College. I will link this blog to many of my blogs at Science20. It is the responsible - and not fun - thing to do.
I will remain proud that my proposal was specific, so it had the ability to be wrong.
A proposal needs but one fault to be wrong. The GEM unification proposal had several. Some of the deadly sins were committed by using the hypercomplex product, a move away from quaternions, my area of specialty.
Kepler's old equal area swept out in equal time for planetary motion is now understood as a statement that angular momentum is conserved for gravitational systems. A Lagrangian is every way energy can be traded inside a box. If one can spot a symmetry in a Lagrangian, that symmetry is linked to a conserved quantity. To conserve angular momentum, one must be able to rotate the Lagrangian in space and show that the result does not change so that angular momentum is conserved.
There are two current coupling terms in the GEM unification proposal:
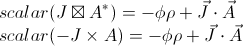
In a rotation, the phi and rho are unchanged. The dot product is the cosine of the angle between the two 3-vectors times the magnitude of those 3-vectors. The angle between the two 3-vectors and their magnitudes are unchanged by a spatial rotation. There is no problem with rotation for either current coupling term.
It is the contraction of the field strength tensors that causes the problem with angular momentum conservation. This is the field strength tensor contraction:
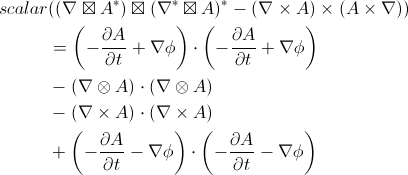
Three out of the four terms are invariant under a rotation. The first and fourth terms behave like polar vectors that happen to point in different directions due to the sign on the gradient of phi. The dot product will square the magnitude of these two vectors times the cosine of the angle between them as happened in the current coupling term.
It takes more work to see the dot product of a curl with itself is invariant under a rotation. If this were a cross product, then one would say the cross product is the area formed by making a parallelogram out of the two vectors, and the area will not change under rotation. The area can be calculated by taking the product of the magnitudes of each vector times the sine of the angle between the two 3-vectors. The dot product of that will not changed by rotation either.
The invariance of the norm of a curl under a rotation can all be shown symbolically with quaternions. A rotation involves pre- and post-multiplying by a unit quaternion. Rotate the parts that go into a curl:
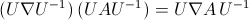
The curl is only the antisymmetric part of a quaternion product:
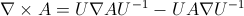
For the dot product:
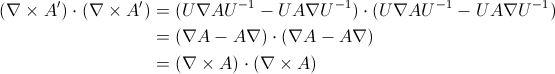
The presence or absence of of these U's are not going to change this result which technically is the 3-vector part of the norm of a quaternion. The norm of the unitary U's is one.
This is just some detail of the widely known, very old observation: the dot product of a curl is invariant under a spatial rotation.
Now consider the symmetric curl. Hypercomplex numbers do not form a division algebra. More germain is that the hypercomplex numbers do not form a normed algebra. Why is that? With all those positive signs and no element of antisymmetry, it is not possible to pack all of the values present into one real number slot as happens with the norm of a quaternion. For quaternions, if q=(a, B), q* q = (a^2 + B.B, 0, 0 0). One can generate the same first term with hypercomplex numbers, but there are also terms in the other slots. There is no way to get those terms to bow out and have the result be only a real number, a central property of a norm.
Hypercomplex numbers are going to be painful to work with. One simple approach is to use plain old numbers and see how the numbers behave. Symbols are abstractions of numbers. Using randomly chosen numbers represent a concrete example. A number of years ago, I wrote a few programs in C so I could play with quaternions at the command line. If you are familiar with the command line, it is an odd way to show that the dot product of a cross product is invariant under a rotation:
% q_x_odd 1 2 3 4 3 2 3 1 | q_square
-117.0000000000000000 0.0000000000000000 0.0000000000000000 0.0000000000000000
% q_x `q_normalize 2 -4 2 -2` 1 2 3 4 | q_x `q_normalize 2 4 -2 2` | tee q1r
1.0000000000000000 3.4285714285714284 -1.8571428571428568 -3.7142857142857135
[notice the first term is one, while the others have changed. The results is stored in q1r]
% q_x `q_normalize 2 -4 2 -2` 3 2 3 1 | q_x `q_normalize 2 4 -2 2` | tee q2r
2.9999999999999991 0.8571428571428570 -2.7142857142857135 -2.4285714285714279
[same story with the result stored in q2r]
% q_x_odd `cat q1r` `cat q2r` | q_square-116.9999999999999005 0.0000000000000000 0.0000000000000000 0.0000000000000000
Within rounding error caused from using with finite approximations, the cross product (q_x_odd) is not changed by the rotations.
Now we try out the same calculation with the hypercomplex product:
% q_sym_cross 1 2 3 4 3 2 3 1 | q2_square
469.0000000000000000 240.0000000000000000 360.0000000000000000 300.0000000000000000
% q_sym_cross `cat q1r` `cat q2r` | q2_square
464.1720116618071756 250.8754685547686449 -318.0424822990417510 -335.9100374843812347
The first terms are different. A rotation changes the result. A symmetric cross product changes under a rotation. The precise folks will note the example with the numbers is about a symmetric cross product, not the symmetric curl. While I could invest in figuring out how to show that for a symmetric curl, it is the underlying algebra of hypercomplex numbers that creates this problem. That problem will not go away. In poker, one needs to know when to fold 'em.
Because the square of a symmetric curl is not invariant under a spatial rotation, angular momentum is not conserved. That is a deal breaker.
Gauge symmetry was an important part of my proposal. Why? In EM, the U(1) gauge symmetry is why there is electric charge conservation. In a GEM proposal for the gravity part, there would need to be a gauge symmetry for mass charge conservation. Once again it is the symmetric curl that creates the problem. Here is the EM magnetic field:
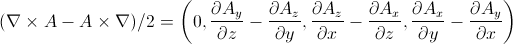
Now do the gauge transformation on one of the ordering of the derivative and potential:
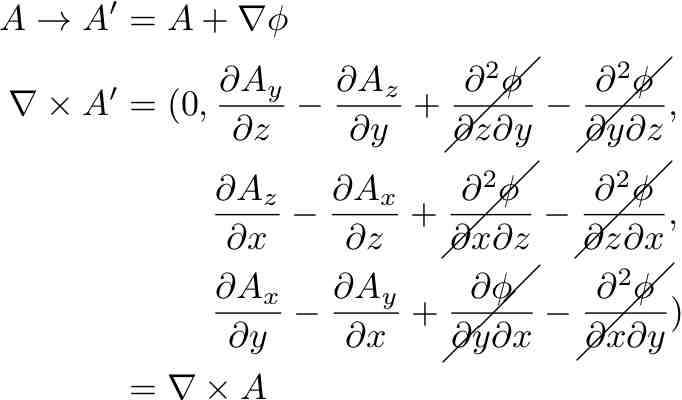
Repeat the process, but replace any minus sign with a plus.
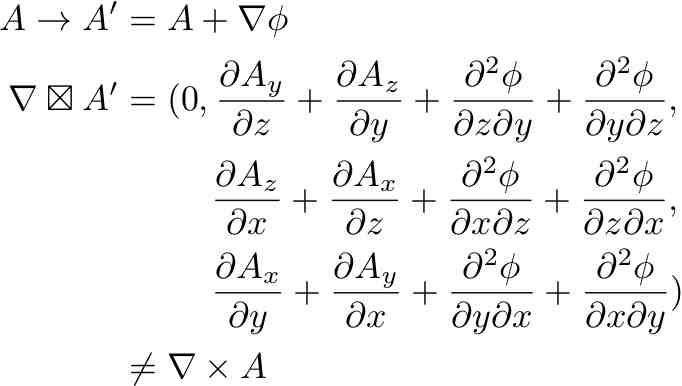
Oops, the gauge field is not going to cancel out. The symmetric b field is not invariant under a gauge transformation. In my interpretation of the proposal, that would mean mass is not conserved. That is a deal breaker.
<??? marking the following as a questionable reason for rescinding the proposal>
The GEM unification proposal would be resistant to quantization. One key step in quantization is to take a set of field equations and invert those field equations to generate propagators of the quanta in the field. This requires one to pick a gauge. The propagator is then used in perturbation calculations in quantum field theory.
One of the most powerful properties of quaternions is that they are a division algebra. Imagine one has a set of field equations formed by taking the operators and forming the necessary products using the quaternion division algebra. It would be the case that the field equations could be inverted. One would still need to pick a gauge for a gauge invariant field proposal to do a calculation. Knowing an inverse exists strikes me as a stronger foundation for quantum field theory. Note that I have never read anyone with credentials who discussed this issue, so it could well be a vaporware-observation. What people do is consider field equations over a division algebra (usually complex numbers). I am thinking about forming the field equations with a division algebra. I doubt I will ever have the math chops to establish any technical advantages to using a 4D division algebra to form the equations.
The GEM unification proposal uses both quaternion and hypercomplex algebras. The hypercomplex numbers do not form a division algebra. As such, the hunt for a propagator may well be in vain.
</???>
The t-shirt claims there is "no stinkin' Higgs". There most certainly is a new particle at 126 GeV. There is much to learn about this new particle. We need to establish that the spin is zero based on data, not on our expectations. The channels that have that information are hard for even the LHC to collect. I have no idea what can be done to tell the difference between a spin zero Higgs and some odd spin 0 composite particle.
My own reservations about the Higgs particle discovery are immaterial for the blog at hand. In the GEM unification proposal, there was a cute cancellation of terms in the gravity part with those for the EM part. It was so cute, I hope it would provide an algebraic reason why inertial mass is exactly equal to gravitational mass, a central assertion in general relativity. There was never a link to providing mass to specificaly to the W or Z particles. In this claim, there was not enough there there.
One of the early experimental conformations of general relativity was that light bends around the Sun twice as much as Newtonian theory predicts. In the GEM unification proposal, the exponential metric matches the current data and predicts 12% more bending than general relativity does at the next level of precision. No tests at the resolution of microarcseconds are planned. As a force equation, the GEM proposal gets the static Newtonian solution right. Since there are more terms in the GEM proposal force equations, it has the capacity to get the dynamic force calculation for a photon cruising by the Sun. At this time, I don't know how to do such a calculation. It is my responsibility to figure out the math. This may be an error by omission that is beyond my reach currently. Or not. A consistent proposal must be able to show the same results in the force form.
The Future of My Research
I still believe that the rank two field equations of general relativity will be replaced someday by a rank 1 field proposal. As a personal belief, I do not ask that you share such an article of faith in this research direction.
There are speculative alternatives to what is on the t-shirt. One could imagine that for classical gravitational systems, the symmetric b field is effectively zero. A different proposal could claim that breaking gauge symmetry is not a bug but is a feature. I will investigate these and other possibilities. I have no idea if any will pan out. I expect that none will. Most of my limited research time currently involves working on a software project for analytic animations on an Android phone. It will be years if at all before I might formulate a new proposal.
As I previously stated, any new proposal must:
* Have rotational symmetry to conserve angular momentum
* Have gauge symmetry to conserve mass
* Have a metric solution
* Have a force equation whose static solution is equivalent to Newtonian theory, but whose dynamic force is twice Newton's
* Have a symbolic math program backing up all claims
Should anyone ever offer a variation on the GEM unification proposal, I would need the same criteria met, including the Mathematica/Maple/Sage supporting notebook.
Thanks to the Critics
This was a tough relationship in many cases. At this distance from the blogs, I take the bottom line, which is to rescind the proposal and do the work to make this blog widely linked. The dustbin of history is calling.
Comments
I have blocked comments for this blog because it is my eulogy to this body of work. I have no interest in hearing other peoples favorite reason for rescinding this proposal. If you wish to send constructive comments, I am easy to reach (sweetser@alum.mit.edu).
Next month or two: Artifacts from the Rescinded GEM Proposal





Comments