So much action happens with with interaction term of a Lagrangian, it is easy for those not initiated into the refined arts of field theory to skip over issues. In this blog I will dive into the details of a vector current coupling which should indicate why a spin 1 field must be associated with the interaction. The next blog will follow a similar road for a set of symmetric rank 2 tensors that requires a spin 2 field. The final blog examines how charges attract or repel for either spin. Hopefully I will include critical caveats for these subjects. If not, the comments may have a pearl or two worth reading.
I should probably surround the entire blog with the <begin ???> <end ???> tags. I have exchanged a few emails ahead of time with Henry. Feynman started the key chapter with a small Feynman diagram, and ended it with a discussion of the rules for angular momentum in quantum mechanics, so I presumed quantum mechanics throughout. Most of the analysis that follows could just as well be classical EM. It does raise a question of interpretation: how and where would the differences be in a completely classical analysis versus a quantum one? One way would be in the description of the potential A: if they were operators action on a wave function, the analysis would be quantum mechanical. If the potential A were functions, then the analysis is classical. That kind of detail is missing. Feynman does talk about photons, the quanta of EM, and virtual photons throughout. If one was "in the room", one would probably just know whether he was doing QED riffs or doing a classical analysis. Since the book is devoted to thinking about a quantum theory of gravity, I see it as quantum theory through and through. Henry sees the classical equations as, well, classical. Feynman does talk of "currents, which are source operators", indicating a quantum slant, but I have tried to remove most references to photons because it is fun to view the analysis as classical and/or quantum mechanical.
The fundamental forces in the Standard Model - EM, the weak, and the strong force - all are spin 1 fields. There is compelling but not absolutely certain logic that gravity is mediated by a spin 2 field. Richard Feynman was one of the three originators of quantum electrodynamics (QED). Because the coupling constant for EM is small, perturbation theory can be used to make valuable calculations. He reasoned that gravity might be even easier to quantize given the coupling constant would be orders of magnitude smaller. There are a number of technical reasons why this has not been the case, the non-linearity of the rank 2 field theory being a common cause.
This blog will walk slowly through Feynman's analysis of spin 1 and EM ("Feynman Lectures on Gravitation", pages 29-35). Since Feynman and the majority of readers use tensors, I will write out these equations that way too. A minor alteration from the lecture notes will be done, change the index ordering from 4321 to 4123.
In order for this author to really own the calculations, I will also write the expressions using quaternions, marking them with a QQQ. If one fears Greek letters, this is the way to go :-) In most cases, one can conclude a few electrons were wasted. A more sophisticated comment would be to say the quaternions were isomorphic to the tensor notation. There is one step where quaternions may provide a bit of clarity lost in the tensor approach.
The interaction term in EM is the contraction of two 4-vectors, one for the source current J, the other for the potential field A. The fist step is to "take the Fourier transformation and use the momentum-space representation." [Clarification: I will use a tilde, the little squiggle, it indicate that a 4-vector is in the momentum space instead of the far more common position space.]

Quite the first step, but this is Feynman lecturing to grad students. Let me back up a step. Here is the Maxwell equations written in the Lorenz gauge [in position space]:
%20A_{\mu}%20=%20J_{\mu}\\%20\\%20QQQ:~&scalar%20\left[%20\nabla%20\times%20\nabla%20\right]%20\times%20A%20=%20\left(\frac{\partial^2}{\partial%20t}%20-%20\nabla^2%20\right)%20A%20=%20J%20\end{align*})
The analysis presumes one is working in the Lorenz gauge. It is this equation one take the Fourier transform. The k2 is thus doing the job of the those derivatives, which gets the name the D'Alembertian operator.
The careful reader will notice that the Fourier transform into the momentum representation includes a sign flip [corrected from -1/k2]:
%20\rightarrow%20-k^2)
That minus sign is essential. It will eventually lead to like charges repelling. Where does it come from? Consider a plane EM wave:
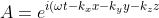})
Notice the factor of i. The Fourier transform will pull down a factor of i for each k. Doing that twice generates the factor of -1.
What is this k? It is call the wave number. It is an inverse wavelength. You could also consider it to be like a spatial frequency. In the magic that is a Fourier transform of the Maxwell equations in the Lorenz gauge, the wave 4-vector does the work of the 4-derivative.
Feynman includes a small diagram:
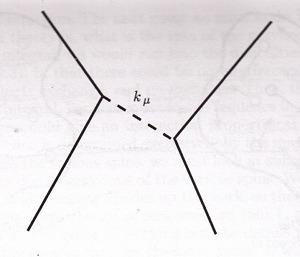

The wave number vector is doing the work of a propagator in QED, at least in the picture.
The interaction term can now be viewed as a current-current interaction:

The focus is on the invariant terms. The vector terms in the quaternion expression will play a role later, so the early appearance is foreshadowing.
He decides to pick a coordinate bases in the momentum representation to make things easier to write out in components. Here are the players in their component notation:
%20\quad%20eq.~%203.2.3-4\\%20k^{\mu}%20&=%20(\omega,%200,%200,%20\kappa)\\%20k^2%20&=%20\omega^2%20-%20\kappa^2\\%20\\%20QQQ:~~%20\tilde{J}%20&=%20(\tilde{\rho},%20\tilde{J}_x,%20\tilde{J}_y,%20\tilde{J}_z)\\%20QQQ:~~%20k%20&=%20(\omega,%200,%200,%20\kappa)\\%20QQQ:~~%20scalar%20\left[%20k%20\times%20k%20\right]%20&=%20\omega^2%20-%20\kappa^2)
A detail tripped me up. The currents are real in the x, y, and z direction. He has chosen a coordinate basis in the Fourier transformation such that there is a non-zero wave number along the z axis, but there are zeroes for x and y. Nothing has been changed about the physical system. It was his choice: stack all the changes along z.
Confession: I really should be using 1, 2, 3, not x, y, z. One needs the freedom of the far more abstract 1, 2, 3 to make sure a sufficiently clever choice can be made for the coordinate basis to have two out of three be equal to zero. I hope the reader will tolerate my desire for something concrete as x, y, and z in this otherwise abstract discussion.
Rewrite the current-current coupling using these components:
%20\quad%20eq.%20~3.2.5\\%20\\%20\\%20QQQ:%20scalar%20\left[%20-\frac{1}{k^2}%20\tilde{J}'%20\times%20\tilde{J}%20\right]%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{\rho}'%20\tilde{\rho}%20-%20\tilde{J}'_x%20\tilde{J}_x%20-%20\tilde{J}'_y%20\tilde{J}_y%20-%20\tilde{J}'_z%20\tilde{J}_z%20))
Electric charge is conserved. In momentum space, this is a contraction of the wave number 4-vector and the 4-current:
%20=%200\\%20\tilde{J}_3%20&=%20\frac{\omega}{\kappa}%20\tilde{J}_4%20\\%20\\%20QQQ:~~%20scalar[k%20\times%20\tilde{J}]%20&=%20\omega%20\tilde{\rho}%20-%20\kappa%20\tilde{J}_z%20=%200%20\\%20QQQ:~~%20\tilde{J}_z%20&=%20\frac{\omega}{\kappa}%20\tilde{\rho})
Here is a detail I am missing. Back in the usual representation, one writes charge conservation like so:
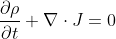
I am missing a subtlety (I am not doubting the result).
Use the conservation of charge to eliminate the current in the direction of the z axis:
%20\\%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_4%20\tilde{J}_4%20-%20\tilde{J}'_3%20\tilde{J}_3)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_1%20\tilde{J}_1%20+%20\tilde{J}'_2%20\tilde{J}_2)%20\\%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_4%20\tilde{J}_4%20-%20\frac{\omega^2}{\kappa^2}%20\tilde{J}'_4%20\tilde{J}_4)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_1%20\tilde{J}_1%20+%20\tilde{J}'_2%20\tilde{J}_2)%20\\%20&=%20-%20\frac{\kappa^2%20-%20\omega^2}{\kappa^2(\omega^2%20-%20\kappa^2)}(\tilde{J}'_4%20\tilde{J}_4)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_1%20\tilde{J}_1%20+%20\tilde{J}'_2%20\tilde{J}_2)%20\\%20&=%20\frac{1}{\kappa^2}(\tilde{J}'_4%20\tilde{J}_4)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_1%20\tilde{J}_1%20+%20\tilde{J}'_2%20\tilde{J}_2)%20\end{align*})
QQQ%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{\rho}'%20\tilde{\rho}%20-%20\tilde{J}'_x%20\tilde{J}_x%20-%20\tilde{J}'_y%20\tilde{J}_y%20-%20\tilde{J}'_z%20\tilde{J}_z%20)%20\\%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{\rho}'%20\tilde{\rho}%20-%20\tilde{J}'_z%20\tilde{J}_z)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_x%20\tilde{J}_x%20+%20\tilde{J}'_y%20\tilde{J}_y)%20\\%20&=%20-%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{\rho}'%20\tilde{\rho}%20-%20\frac{\omega}{\kappa}%20\tilde{\rho}'%20\tilde{\rho})%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_x%20\tilde{J}_x%20+%20\tilde{J}'_y%20\tilde{J}_y)%20\\%20&=%20-%20\frac{\kappa^2%20-%20\omega^2}{\kappa^2(\omega^2%20-%20\kappa^2)}(\tilde{\rho}'%20\tilde{\rho}%20)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_x%20\tilde{J}_x%20+%20\tilde{J}'_y%20\tilde{J}_y)%20\\%20&=%20\frac{1}{\kappa^2}(\tilde{\rho}%20\tilde{\rho}'%20)%20+%20\frac{1}{\omega^2%20-%20\kappa^2}(\tilde{J}'_x%20\tilde{J}_x%20+%20\tilde{J}'_y%20\tilde{J}_y)%20\end{align*})
See what is not there. There are no terms involving z, it was eliminated as promised. There is no frequency omega in the first term. Omega is the stand-in for a derivative with respect to time, thus the first term has no changes with respect to time. That is not crazy. It is Coulomb's law which is also instantaneous. This is a great approximation for low velocities. The other terms are relativistic corrections. Together, the instantaneous term plus the corrections make for an expression that is invariant under a Lorentz transformation.
The force in EM can only be carried by virtual photons. Why? A darn good question that may generate some discussion. One reason is that nothing can go faster than the speed of light which applies to light too. No work can be done in the direction of motion, the z axis in this choice of the representation, leaving all the work to be done along x and y.
The next step is to take plane polarized waves and combine them to make circular polarizations:
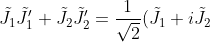%20\frac{1}{\sqrt{2}}%20(\tilde{J}'_1%20+%20i%20\tilde{J}'_2)^*%20+%20\frac{1}{\sqrt{2}}%20(\tilde{J}_1%20-%20i%20\tilde{J}_2)%20\frac{1}{\sqrt{2}}%20(\tilde{J}'_1%20-%20i%20\tilde{J}'_2)^*%20\\%20eq.%20~3.2.10)
It took me a little time to see all the imaginary parts canceled each other nicely. This new polarization is useful when thinking about rotation around 3, it is just a rotation by an angle theta. The two phases are exp(i theta), exp(-i theta).
The analysis has a twist when done with quaternions.
%20&=%20((0,%20\tilde{J}_x,%20\tilde{J}_y,%200)%20\times%20(0,%20-\tilde{J}'_x,%20-\tilde{J}'_y,%200)%20+(0,%20-\tilde{J}_x,%20-\tilde{J}_y,%200)%20\times%20(0,%20\tilde{J}'_x,%20\tilde{J}'_y,%200)%20)/2%20\\%20&=(\tilde{J}_x%20\tilde{J}'_x%20+%20\tilde{J}_y%20\tilde{J}'_y,%200,%200,%20\tilde{J}_x%20\tilde{J}'_y%20-%20\tilde{J}_y%20\tilde{J}'_x)%20+(\tilde{J}_x%20\tilde{J}'_x%20+%20\tilde{J}_y%20\tilde{J}'_y,%200,%200,%20-\tilde{J}_x%20\tilde{J}'_y%20+%20\tilde{J}_y%20\tilde{J}'_x)%20\end{align*})
The product of the x and y current move over and occupy the z current [Clarification: it is the cross product that does this in the quaternion representation]. They do so because there are three imaginary numbers built into quaternions. To my eye, that is a good thing. The wave number was chosen so that x and y are zero and all the interaction terms happen along z. This shows how the x and y can contribute to z as relativistic corrections.
I scrubbed many (not all) reference to photons the quanta of EM so one could view this analysis as being classical if one so chooses. The following quote indicates how Feynman makes a connection:
The quantum-mechanical rules describing the behavior of system under rotations tell us that systems having this property are in a state of unique angular momentum; the photons that change in phase as exp(i theta) have an angular momentum projection 1, and the others a projection -1.
This quote at the end of this analysis has always been my basis for the statement that a vector current coupling implies a spin 1 field for a vector current interaction.
Doug
Snarky puzzle: Figure out how to represent any quaternion using 3D rotations and one complex number.
Google+ hangout: 11:00-11:45pm Eastern time, Tuesday-Wednesday. http://gplus.to/sweetser
This could be an efficient way to exchange a few ideas. If you have a question or two, hangout.
Next Monday/Tuesday: Spinning the Interaction Story: Spin 2 (2/3)




Comments