Known unknowns
I am sure I am going to be criticised for the down-to-earth definition that follows - some of my colleagues, and especially the friends I'll meet in Banff, are rather nuanced on the topic. Yet we need to be pragmatic here, so here is my simple definition: a systematic uncertainty is a source of imprecision in the measurement of some quantity, which results from the way the measurement is carried out.
A systematic uncertainty is a bias that sneaks into your estimate, changing it in an unpredictable way. It is a so-called "error of the second kind", when the first kind of error is due to statistical fluctuations (there is also a third kind of error due to the imprecise definition of the quantity you claim you are measuring). Statistical uncertainties are simple to estimate and cause little trouble to experimentalists; systematics are all another matter!
There are cases when a systematic uncertainty is there unbeknownst to you: such "unknown unknowns" are scary, because they can really lead you to report a really wrong result. More frequently you know a systematic error is there (you know there is potentially a shift), but you do not know its size, nor if it raised or lowered the measurement you got. In that case you can try and size up the effect, and account it in your reported uncertainty bars. The skill of experimental physicists often can be gauged by how careful they are in beating down sources of systematic uncertainty, and in devising cunning ways to size them up precisely.
Systematics and you
If you are not an experimental physicist, I suppose you may live a comfortable life oblivious of the intricacies connected with providing a precise estimate of the uncertainty of a measurement. But chances are you do measure things now and then, and I bet when you do you are also interested, or maybe just curious, on how precise the measurement is. Let us make a few examples.
1 - You step on your digital scale every morning, and the scale returns your weight in tenths of a kilogram (say). One morning your reported weight is 79.5 kg - below your "warning region" of 80 kg and more, so you are happy. You eat normally, and yet the next day you read 80.3. You are a bit annoyed, as this implies you will have to watch what you eat for the next few days (a self-inflicted rule). So you wonder how precise is that measurement. Could your weight be actually the same of yesterday, and the reported number be an overestimate?
2 - You are driving home after a long day out for work, and your navigator claims there are 50 miles left to drive. There is one gas station left between you and your destination, and the car display shows you have 60 miles left of gas before you run out. You would really love to avoid to refuel, leaving the errand for tomorrow. Should you trust the measurement, or maybe should you instead consider the possibility that the amount of gas left in the tank has been overestimated?
3 - You need to check that the 82-inches-long desk you are about to order online is going to fit in the space along the wall in your office, but you have no other way to measure the wall length than to use your hand. You are pretty sure your span is of 8 inches, and you measure the length as 10.5 spans, so you figure you have 84 inches of free wall space. This calls for questioning whether your measurement is precise enough, doesn't it?
In all cases above, you are forced to call to question the accuracy of your measurement. What you would really need, in order to take an impactful decision (ignore the diet? stop at the gas station? keep looking for smaller desks?), is an estimate of the probability that the measurement you got can be wrong by an amount sufficient to make you change your mind with respect to the action you would take if the measurement were exact.
In physics we actually do not need to take decisions - we stop at reporting measurements with their estimated uncertainties; but nonetheless, we are really interested to include in our estimate of uncertainties all possible effects liable to make them larger than we thought. The reason why we are so obsessed by the uncertainties we report is that the precision of our determinations of physical parameters is often the single most important gauge of our success as experimentalists.
A particle physics example: the W boson mass saga
Take the W boson as a telling example. The UA1 experiment discovered that particle in 1983, and since then all high-energy physics experiments producing it (UA2, CDF, DZERO, the four LEP experiments, and later the LHC experiments) continued to publish more and more precise estimates of the particle's mass. The estimated uncertainty went down from a couple of GeV in the eighties to less than 100 MeV in the early nineties, then 30 MeV at the turn of the millennium, and is now more than twice smaller than that. All this is extremely interesting to physicists because of the special role of the W boson in electroweak theory, and I would need a full article just to explain that concept in detail, so let us leave that for another day.
As I said above, in general experimental physicists will pride themselves of having reached a higher precision on an important physical parameter, such as the W mass. But what happens if later on they are proven wrong? This may be embarrassing. Take the recent history of the W mass for a glaring example.
After 10 years of painstaking studies, CDF last year shocked the world of fundamental science by publishing an estimate of the W mass which was both extremely precise - a mere 9 MeV total uncertainty, in the face of the runner up measurement which had a reported precision of 19 MeV - and way above most of the previous estimates (see picture below).
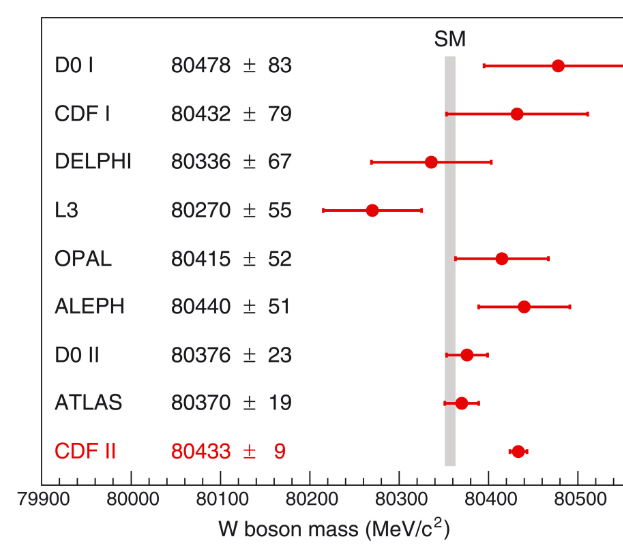
More recently, ATLAS produced an improved measurement which seemed to disprove the CDF "impossibly precise" estimate and central value. Of course, if the true W boson mass were exactly the value reported by ATLAS we would then know that the CDF estimate underestimated its uncertaintiy, as a shift by seven standard deviations cannot arise by chance. This would disqualify the credibility of the CDF analyzers. On the other hand, we are not there yet - ATLAS might be wrong instead. Time will tell; the involved people will safely retire from full professorship by then, so the establishment of factual truth will bear no practical consequences. But I guess you got the point: experimental physicists are obsessed with the estimate of uncertainties, because of pride, credibility prestige, if you will; I tend to believe it is instead because of love for scientific truth.
The workshop, Machine Learning, and my contribution
All the above may sound fascinating, or terribly boring; in the latter case you are already browsing elsewhere, so I will now address the twenty-three of you who have stuck here. The Banff workshop will get to the same place some physicists and statisticians who have become true experts of the matter of estimating and beating down systematic uncertainties; and in addition, I will be there, too.
The topic of assessing systematic uncertainties in physics measurements has made giant leaps in the past thirty years - roughly the time I have been around as an experimental physicist. I remember that thirty years ago it looked okay to assess a systematic uncertainty by taking the half-difference of the result obtained by using one model or an alternative one: how many of you have heard of the infamous "half of Pythia minus Herwig"? Such rudimentary techniques were all we had back then, but over time we have grown more sophisticated.
While the theory of measurement still has lots to offer, so that heated debates between statisticians and physicists are going to be the delight of the coming week in Banff, there is a new player today: machine learning. Since we employ machine learning methods to extract information from our data, you could well expect that we need to assess what uncertainties are brought in by this new system. Strangely, though, that is not actually the focus of the workshop when it comes to machine learning. In fact, the data crunching performed by machines still allows for very standard methods for estimations of biases our measurements incur in due to the extraction methods.
Instead, machine learning today offers ways to reduce the impact of systematic uncertainties in our measurements. By finding higher-dimensional representations of our data that are less sensitive to unknown biases and shifts, those tools can produce summary statistics that are more robust, and consequently results that are more precise. That is precisely the contribution I will give to the workshop. I will discuss the recent trends in this area of studies, and present the work Lukas Layer and I have done in reproducing a CMS physics measurement by employing a machine-learning technique that lets the neural network "learn" how to reduce our systematic uncertainties. If I have time I will describe the technique in this column in the near future. If not, you can get a peek at our work at this link.
---
Tommaso Dorigo is an experimental particle physicist, who works for the INFN at the University of Padova, and collaborates with the CMS and the SWGO experiments. He is the president of the USERN organization ), the coordinator of the MODE collaboration , and an editor of the Elsevier journals "Reviews in Physics" and "Physics Open". In 2016 he published the book "Anomaly! Collider physics and the quest for new phenomena at Fermilab".





Comments