
The article is a proceedings of the Elba conference named "Frontier Detectors for Frontier Physics", a very famous event that takes place every three years in the Biodola gulf of the Elba island, off the coast of Tuscany. Besides the interest and its top-level nature, the conference is famous for the amazing food that guests are treated with at the Hermitage hotel, an awesome 5-star resort.
I had the pleasure to attend the conference only three times; the first time was in 2000, when I presented a poster on the upgrade of the muon system for the CDF experiment at the Fermilab Tevatron collider. Posters are usually not a significant addition to one's CV, but in that case the proceedings paper I wrote ended up being cited widely as the main source of the description of the Run 2 muon system of CDF, so that it currently has 85 citations - not really bad for a single-author proceedings paper! So I do hope that the new article I am discussing here, which is also the summary of a poster, will end up on a similar path.
Anyway, back to the summary of the summary. In the poster, and in the proceedings, I explained how we are getting equipped to exploit differentiable programming for the end-to-end optimization of particle detectors. As particle detectors are extremely complex instruments, and the design of these instruments is considered a subtle art that takes decades to master, the above sentence is little short of an insult to anybody who considers herself a detector expert.
So it is important to explain that the new AI-powered methods -which rely on surrogate models of the data-generating processes, which are typically stochastic in nature and thus impossible to be included in a differentiable model (which is key to gradient-based optimization) - are meant to be instruments in the hands of the detector builder, not plug-and-play tools that invite her retirement. With those tools, it will become vastly more efficient and quick to test different layouts and determine, within specific choices for detection technology and specifications, what geometric arrangements work best and how constraints can best be accommodated in the design.
In the article I mentioned only a few of the ongoing projects. Probably the most impactful and advanced of these is the optimization of the LHCb electromagnetic calorimeter, which will drive the layout of the photomultiplier tubes in that detector, which is undergoing an upgrade for the high-luminosity phase of the LHC.
On the other hand, a number of other use cases, no less interesting, are appearing at the horizon: the optimization of the layout of Cherenkov tanks to detect ultra-energy gamma rays with the SWGO detector array, the design of neutron moderators for the LEGEND-1000 neutrinoless double beta decay experiment, the optimization of the electromagnetic calorimeter for the detector instrumenting a future muon collider, and many others. The MODE collaboration (https://mode-collaboration.github.io) is leading the research in this interesting area of R&D, and it is growing in size - with computer scientists and physicists joining from a number of institutes around the world.
To show the kind of work we are doing, I am pasting below an animated GIF that shows how the positioning of Cherenkov tanks of the SWGO array can be optimized automatically, once one creates a differentiable pipeline. The concept is shown in the graph below:
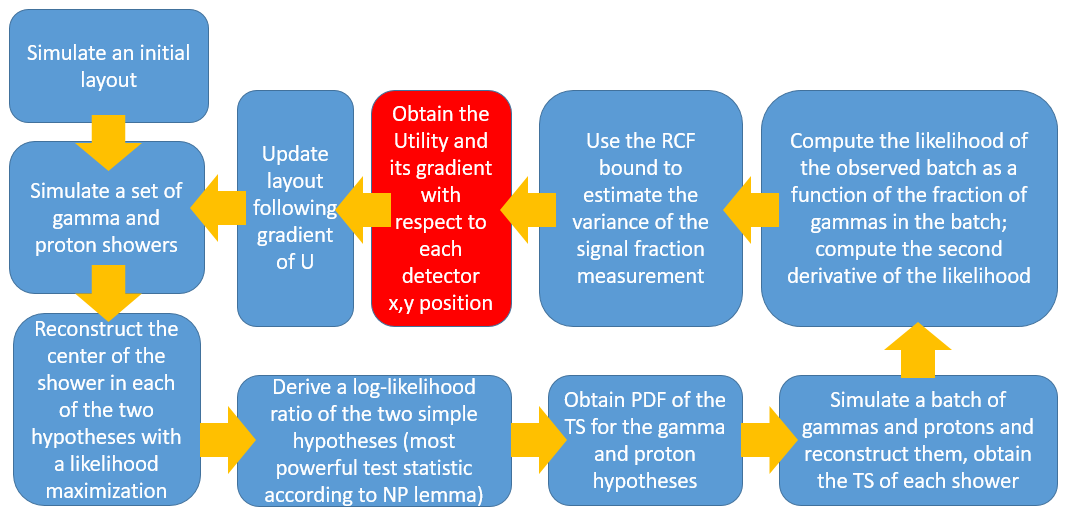
As you can see, one needs to simulate a layout, then simulate the physics (in this case, high-energy gamma rays and high-energy cosmic ray protons, the background to be distinguished by the experiment), create a test statistic that distinguishes gammas from protons, and then compute, with the help of batches of data, how well the signal can be measured - and a resulting utility function. If one can then compute the derivative of the utility function with respect to the position of all the detectors, the system may learn the best configuration by stochastic gradient descent.
The GIF below shows several control diagnostics, but you can probably focus on the second graph from the left, which shows black points where the detectors are positioned on the ground (a vast area at high altitude in Chile), and smaller coloured points showing the position of gamma and proton showers in each batch of events during the optimization cycle. As you can see, the system realizes that the detectors can be fruitfully driven farther apart to intercept a larger number of showers, without reducing the precision on the measurement of those close to the center and improving the overall statistical power of the measurement.

Needless to say, putting together the code that pulls off this trick is not easy, but it is extremely satisfying to then observe how the machine interprets its job of finding optimal solutions!





Comments