The number of 3-node, 3-edge connected subgraphs in a random, scale-free network of N nodes scales as N0 (=1). No matter how big your network grows, you're going to have a roughly constant number of 3-node, 3-edge subgraphs that depends only on the ratio of edges to nodes.
Let's back up a minute before we see why this counterintuitive result is so and what it means. Imagine that we have a network made up of N nodes connected by E edges. You can start out with two nodes connected by one edge:
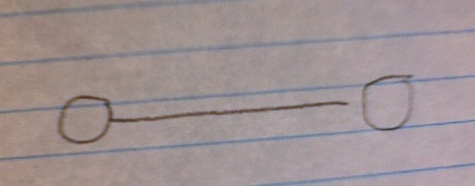
Your edge-node ratio here is obviously 0.5. Let's say that you gradually increase the size of your network, adding more edges and nodes (assigning the connections randomly), but always keeping an edge-to-node ratio of 0.5.
As your network grows, you start seeing subgraphs - subsets of three nodes connected by two edges, and three nodes connected by three edges. (As you network grows, you'll naturally also start seeing other subgraphs, with 4 nodes, etc.)
The number of V subgraphs (three node, two edge) scales linearly with the size of your network, as you might intuitively expect: the bigger your network, the more likely you are to find two nodes each connected to a third node.
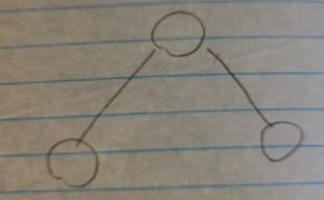
But here's the rub: the number of triangle subgraphs, (three nodes, three edges) stays constant, no matter how large your network grows.
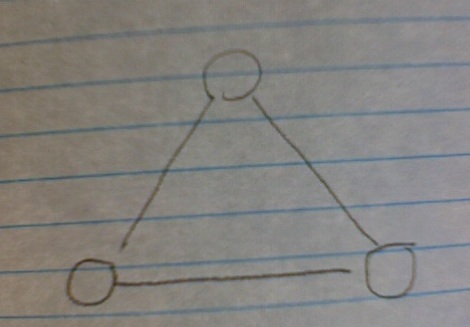
Why? Because, while your V subgraphs scale with N, the likelihood of closing that V subgraph with a third edge (and thus forming a triangle) scales as 1/N. As N grows, it becomes more and more unlikely that a randomly-assigned edge will connect those two nodes needed to close the triangle. So you network can get huge, the number of V nodes gets huge, but, as long as the edge/node ratio stays the same and you're assigning your edges randomly, the number of triangles will not substantially increase.
Why does this matter? Because triangle subgraphs (called feed-forward loops) crop up everywhere in biological networks. Various systems biologists, in particular the Weizmann Institute's Uri Alon, have used this fact to argue that feed-forward loops are doing something special in genetic networks. They crop up much, much more frequently than you would expect in a network with randomly assigned edges.
Of course we know that, like social networks, genetic networks don't have randomly assigned edges. It could be that feed-forward loops don't serve any particularly special function; it could be just an artifact of how these networks are built: if gene A is connected to gene B and gene C, maybe (through some obscure evolutionary process), gene C is very likely to end up connected to gene B, thus forming a triangle. We can see that this is obviously true in social networks: my friends have a high probability of knowing my other friends; that's just how social interactions work.
In biology, there is some evidence, however, that these feed-forward loops are more than just an artifact of making biased connections: there are some clear examples of this particular wiring diagram performing useful functions, functions well-suited to feed-forward loops. In other words, when you see a feed-forward loop in a genetic network, you already have a good idea of what the function of this loop might be. (Although of course you still have to go and test the function of the feed-forward loop to find out for sure.)
In the near future, I'll come back to what feed-forward loops can do. For the time being, here is the much more rigorous version of subgraph scaling (PDF):
Subgraphs in Random Networks, Itzkovitz, Milo, Kashtan, Ziv, and Alon, 2003.






Comments