I just saw the most annoying video about an interesting physics question. Apart from the over the top stereotypical German (supposed to be funny or is he for real?) and arrogant “look how clever we physicists are” attitude, the most annoying is that the really interesting stuff about the question isn’t even mentioned. Arrrggg - how can one be so ignorant?
As he mentions toward the end of the video – if you make it that far without smashing the screen – falling through a tunnel drilled all the way through the center of the earth to the other side results in a so called harmonic motion (neglecting air resistance of course). This basically means that you would move precisely as if you were attached to a spring that obeys Hooke's law.
Why? Well, the mass that still attracts you is proportional to the volume below you, which is proportional to the radius cubed. Gravitational attraction goes proportional to one divided by the radius squared. Thus, the force while falling is all the time simply proportional to the radius that you are at, which is precisely like Hooke’s spring law. But this is only half of the interesting story that should be told.
Why is it that the time you take to fall through to the other side is precisely the same as a satellite needs to circle the earth at just above the surface of the earth (again, all neglecting that there is air and mountains and so on)?
It would be the perfect physics instructor suicide: Shooting a bullet horizontally, giving it the velocity to just circle earth at a constant height, shooting simultaneously with jumping off into the tunnel, the instructor falls and is hit by the bullet just when he reappears at the antipode at the opposite side of the tunnel.
Here a new didactic challenge (to be answered much in the same way as the previous one about Falling Faster than Freefall and the Hawking Lady Gaga Challenge):
Why does this perfect physics instructor suicide work? And please, NO MATHS! I want a "philosophical" answer that shows deeper insight into physics – math trickery is for those who can’t do any better. The answer is almost already given above.
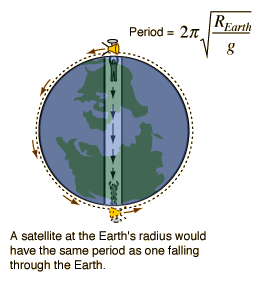
This problem has a good use by the way. The velocity v of a satellite is simply gotten from the centrifugal force v2m/R,and the way half around the earth is simply Pi times the radius R. Thus, the time t for falling through is also simply t = Pi*R/v, the same time as that for the satellite to go around. This way can be easier than getting the time from the harmonic motion, especially for those who do not like infinitesimal calculus but do for whatever reason find the formulas for circular motion and the accompanying forces easy to understand.
UPDATE: Sorry, why not at least give the time - also proves how easy it is this way: With the well known F = m g, it follows v2 = g R, thus t = Pi (R/g)1/2. The radius is about 6370 km and g about 9.8 m/s2, thus the time to fall through is about 42 minutes.
Notice that the Pi is coming from earth's circumference. If going through Hooke’s law instead (which is done here), it takes longer and either you remember less memorable equations or you know how to derive them via integral calculus, and Pi will emerge from the “magic maths”. I like it this way much better, because the the centrifugal (centripetal in the land where no hair is left undivided) is easy to remember as it just expresses the obvious proportionalities involved (OK, now punters will attack me on this point. Whatever.).
--------------------------------------------





Comments