Space is three dimensional: Length, Depth and Height, or X, Y, and Z, that makes three. Since any modest agnostic holds a Multiverse extremely likely though, and moreover also our own universe likely has hidden extra dimensions, nerds keep wondering what life in four dimensional space looks like.

I remember sketching four dimensional watermelon slices as a kid and considering whether one would need three eyes in order to view “stereoscopically”, I mean 4D instead of 3D in four dimensional space. The answer to this is easy: Two eyes are enough, but the retinas of the eyes must be three dimensional, and this seems to be one of the problems with visual imagination of four dimensions. Our brain's visual cortex largely re-maps the retinas. We are hardwired for 3D.

One problem that you may find extremely puzzling yet fun to think about: Helicopters or propeller planes in four dimensions. Why is that a problem?

The two dimensional shapes of triangle, square, and circle all have three dimensional analogues, namely pyramid (tetrahedron), cube, and sphere. The four dimensional analogues are straight forward, and plenty of webpages discuss hyper-shapes like hyper-tetrahedrons, hyper-cubes (tesseracts), and hyper-spheres and how to draw them.

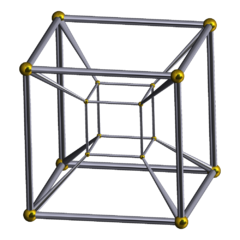A four dimensional Hyper-Cube, also called Tesseract, well, at least the projection of its frame into three dimensional space.

Now one could think that it should be easy to deconstruct a helicopter into its cubes and cones and so on, and then put it together again with the 4D counter parts. But there is a problem: The rotor. Same problem as with propeller planes: In our 3D world, the propeller’s axis points into the direction the plane is heading.

In 3D, the plane of rotation also defines an axis of rotation.

This existence of a unique rotation axis is a “coincidence”. Actually, rotations do not occur around an axis of rotation, but inside the plane of rotation: For example, if in three dimensional space the Z-axis is the rotational axis, the X-Y plane will be the plane of rotation, the plane in which the merry go around sits and turns.

Only in three dimensions is there exactly one dimension left orthogonal to the two dimensional plane of rotation. In four dimensions W, X, Y, and Z, there are all the infinitely many directions inside the W-Z plane that are all orthogonal to the X-Y plane of rotation.

While in three dimensions, the axis of rotation points into the direction that the rotor pushes the plane or helicopter, in four dimensions it is not clear anymore where the plane is going to be headed.

A tesseract rotating in 4D.

So here the puzzle:

A 3D shadow of a 4D torus from yet another webpage about hyper spaces.

How does a hyper-helicopter, one that can fly in four dimensional space, look like? Or better, in case the up versus down distinction and the dimensionality of the ground above which the chopper is supposed to hover are confusing: Design a 4D propeller plane that gets from A to B as straight as a 4D rocket would. (A 4D rocket has no rotating parts, so there are no problems that stop a rocket from going straight.)

The following may help to get to a solution:

In n even dimensions (n = 2, 4, 6...) there are up to n/2 planes of rotation [that] span the space, so a general rotation rotates all points except the origin which is the only fixed point. In n odd dimensions (n = 3, 5, 7, ...) there are (n − 1)/2 planes and angles of rotation, the same as the even dimension one lower [sic]. These do not span the space, but leave [a] line which does not rotate – like the axis of rotation in three dimensions, except rotations do not take place about this line but in multiple planes orthogonal to it. Source

4D Hyper-Rotor?

There should be several solutions: Modified “hyper-axis”, 4D hyper-rotor, need of several hyper-rotors, …? A web-search did not find anything, which is strange – somebody must have thought about this already. Or maybe you will be the first and have your name attached to the design of the 4D hyper-rotor.

REMARK: No, you do not need hyper Navier-Stokes equations. Just think about how blades push molecules.