The physics of nanometer sized bubbles is mysterious and controversial. Gas bubbles in liquids are unstable.[2] Also large air bubbles in water are not stable. Even if we keep them somehow from rising to the surface and popping, the surface tension of the bubble itself presses the air out of the bubble and into the liquid! The physicist calls this ‘Laplace pressure’.[3] We do not notice this with large bubbles. However, with a nanobubble, the Laplace pressure dissolves it in a few micro seconds.

If you have multiple bubbles, the smaller ones get smaller and the bigger ones bigger. This is called Ostwald ripening.[4] Therefore, there is no stable coexistence of many bubbles either. And yet, nanobubbles seem to exist. This is the first, well known mystery, but there is much more.

Nanobubbles on surfaces may live for hours [5,6,7], but also they are still controversial.[8,9] Free nanobubbles, meaning bubbles that just float around without the support of a solid surface, are considerably more controversial.[10] Theory holds them to be meta-stable, meaning that they survive only up to seconds at most. Local gas replenishing mechanisms [11] fail away from surfaces, and they anyway fail the 2nd law of thermodynamics. Some authors [12] admitted this later. [7] How obvious violations of the 2nd law of thermodynamics are nevertheless published tells you something about the state of peer review and scientific publishing.

While the physicists are fighting about whether free nanobubbles exist at all, chemical engineers publish work after work about how free nanobubbles exist in all liquids, stable and not even changing their sizes, leading to very well formed hollow nano shells of many materials. Chemical nano-shell synthesis implies that free nanobubbles are stable without surfactants.

Free nanobubbles seem common, small micro bubbles since before 2003.[13] Yet according to some physicists, such nanobubbles have only “recently been discovered in interfacial physics.”[14,15]

Who is right, who is wrong? Analyzing the hollow nano shells, more mysteries appear, but nano sized bubbles are somehow involved in the production of those pretty hollow shells! How is that possible? That is the big mystery, but let us first enjoy more mysteries as they fall out from the established explanations around how free bubbles supposedly lead to hollow shells.

It is easy to calculate the number N of bubbles (per volume V) that must have been present.[1] The bubbles’ number density n = N/V can be used to compare very different experiments but also very similar runs of the same experiment. The results are astounding. There are several theories available for free nanobubbles, but no available free bubble theory could ever describe the crazy behaviors of the bubble number density n.

SiO shells[16] imply up to 10 bubbles per μm³. This is similar to the number of bubbles derived from observations of ice fractures with about 20 bubbles per μm³.[17] Palladium (Pd)-shells with similar radii imply between 10^-2 and 10^-3 (See Figure).[18] ZnSe microshells [19] imply only 3×10^-4 down to 5×10^-5, almost a million times less than observed in ice fractures. If the bubbles are stable and pre-existed, where are the missing bubbles?

Note well: Not just a few times less, not even just hundreds or thousand times less, but we are looking at an astounding difference of up to millions of times less! (If you came up with a theory that is only wrong by a factor of 100, you would still do thousands of times better than physicists up to now!)


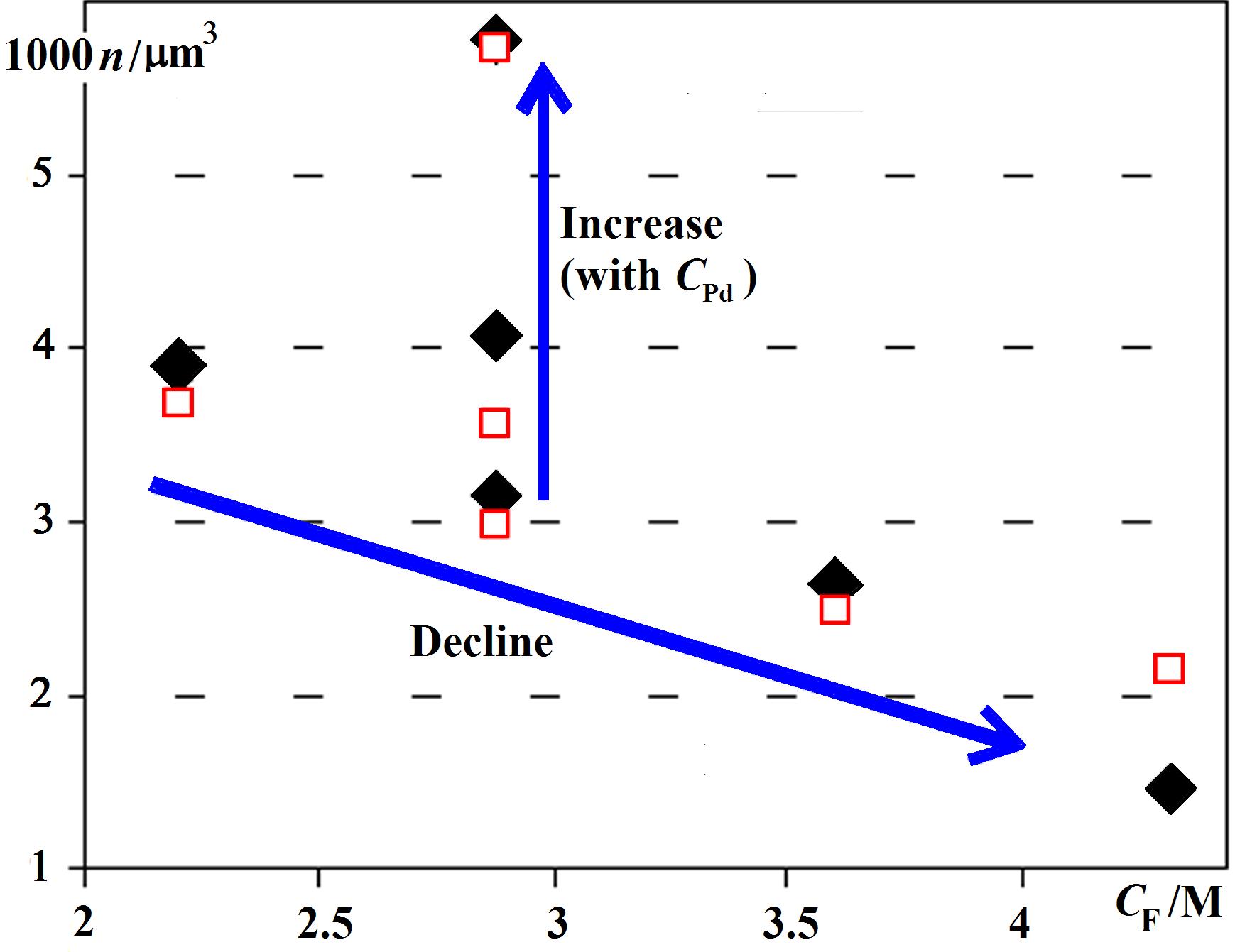Bubble number density n versus concentration C_F of the gas supply necessary for the bubbles: The data are from hollow palladium shells. n = N/V increases with the concentration of the Pd that turns formic acid into gas, as intuitively expected. However, a greater gas supply at constant C_Pd decreases n. Available theories predict n to increase (not decrease) with C_F. Their predicted numbers are off by many orders of magnitude, sometimes by a factor of a million.


The thickness h of the hollow nano shell’s can stay constant although their radius R doubles. Consider that the shell’s material spreads over the bubble surface. The surface is proportional to the radius squared. This implies that the number N of bubbles decreased to a mere 25%. If diffusive gas exchange removes 75% of bubbles in the few minutes before the shell growth starts, the whole size distribution would Ostwald ripen away as discussed above: The population of bubbles would split into a sub-population of bubbles that shrink away completely and a second sub-population of bubbles that grow to about 10 μm, at which point they reach the surface within one minute.

Radius R increases with C_F! However, a larger C_F should provide more gas pressure and smaller radii, a common experimental observation with nanobubbles, all because of their high Laplace pressure. The Laplace pressure ΔP = 2γ/R dominates the bubble pressure and is upheld by the oversaturation ΔC_gas according to Henry’s law (ΔP = K_H). Hence, radius R is proportional 1/ΔC_gas. A straightforward R being proportional to 1/P is indeed reported.

An increase of R with gas concentration is predicted for non-interacting bubbles in a closed volume [20] (similar to shielding [21]). However, those are only meta-stable states. Neither the models’ numbers nor slopes fit the data.

Consider also this: The number density n would need to adjust before the shell growth, as if anticipating a future equilibrium! How on earth do nanobubbles travel in time?

And here is more: Remember that we may expect the shell thickness h to be proportional to the inverse of the squared radius R, because the shell’s material distributes over the shell’s surface. However, R triples while h decreases by a factor of three from 21 down to 7 nanometers. Where is the square dependence? Well, of course it is made up for by the number of bubbles. But again, those numbers do not fit other considerations, and that R is proportional to 1/h is mysterious all by itself.

As already discussed, although C_F increases the gas supply, this counter intuitively decreases n. Something similar happens with the concentration C of the material that builds up the shells, for example the Pd. In the meta-stable many-bubble scenarios, R would depend crucially on C_Pd. The experimental data however could not be clearer: R stays constant when varying C_Pd. How can that even be, given all the complications of the experiments? What kind of mysterious symmetries are we looking at here? They are not at all the symmetries that the established theories predict, but there surely seem to be some mighty interesting symmetries present. The physicist is aroused.

That is a lot of chaos. So the conclusion is obviously that something is very wrong with all the available explanations. However, hollow nano shells are easily synthesized, and nanobubbles are somehow involved. So the main mystery is: What the hell is possibly really going on? Well, stay tuned to this channel, or go have a peek![1]

------------------------

[1] S. Vongehr, S.C. Tang: Formation of Hollow Nano Shells in Solution-based Reactions via Collision Coalescence of Nanobubble-Particle Systems. Nanotechnology 27(24), 245602, 1-6 (2016) doi:10.1088/0957-4484/27/24/245602

[2] Gibbs, J. W. Trans. Conn. Acad. 3, 343 (1878).

[3] Matsumoto, M.&Tanaka, K. Nano bubble—Size dependence of surface tension and inside pressure. Fluid Dynamics Research 40, 546–553(2008).

[4] Schmelzer, J.&Schweitzer, J. F. J. Non-Equilib. Thermodyn. 12, 255-270 (1987).

[5] Zhang, X. H., Khan, A.&Ducker, W. A. A nanoscale gas state. Phys. Rev. Lett. 98, 136101(2007).

[6] Attard, P., Moody, M. P.&Tyrrell, J. W. G. Nanobubbles: the big picture. Physica A 314, 696-705 (2002).

[7] Weijs, J. H. & Lohse. D. Why Surface Nanobubbles Live for Hours. Phys. Rev. Lett. 110, 054501 (2013).

[8] Seddon, J. R. T. & Lohse, D. J. Phys. Condens. Matter 23, 133001 (2011).

[9] Craig, V. S. J. Soft Matter 7, 40–48 (2011).

[10] Plesset, M. S. & Sadhal, S. S. Applied Scientific Research 38, 133-141 (1982).

[11] Brenner, M. P. & Lohse, D. Phys. Rev. Lett. 101, 214505 (2008).

[12] Seddon, J. R. T., Zandvliet, H. J. W. & Lohse, D. Phys. Rev. Lett. 107, 116101 (2011).

[13] Peng, Q., Dong, Y. & Li, Y. Angew. Chem. Int. Ed. 42, 3027-3030 (2003).

[14] Seddon, R. T., Lohse, D., Ducker, W. A. & Craig, V. S. J. A Deliberation on Nanobubbles at Surfaces and in Bulk. ChemPhysChem 13, 2179–2187 (2012) abstract.

[15] Jin, F., Gong, X. J., Ye, J. & Ngai, T. Soft Matter 4, 968 –971 (2008).

[16] Sonae, S.; Ara1, M.; Tada, H. Hydrothermal Synthesis of Silicon-Based Hollow Nanostructures Jap. J. of Appl. Phys. 2012, 51, 06FG06-1-3.

[17] Ohgaki, K.; Khanh, N. Q.; Joden, Y.; Tsuji, A.; Nakagawa, T. Physicochemical Approach to Nanobubble Solutions Chem. Eng. Sci. 2010, 65, 1296 –1300.

[18] Tang, S. C.; Vongehr, S.; Wang, X. Y.; Wang, Y. G.; Meng, X. K. Bubble-assisted growth of hollow palladium nanospheres with structure control allowing very thin shells for highly enhanced catalysis RSC Advances 2014, 4, 13729-13732.

[19] Peng, Q.; Dong, Y.; Li, Y. ZnSe Semiconductor Hollow Microspheres Angew. Chem. Int. Ed. 2003, 42, 3027-3030.

[20] Ward, C. A.; Tikuisis P.; Venter, R. D. J. Appl. Phys. Stability of Bubbles in a Closed Volume of Liquid Gas Solution 1982, 53, 6076-6084.

[21] Weijs, J. H.; Seddon, R. T.; Lohse. D. Diffusive Shielding Stabilizes Bulk Nanobubble Clusters ChemPhysChem 2012, 13, 2197–2204.