One of the disappointments experienced by most mathematics students is that they never get a course in mathematics. They get courses in calculus, algebra, topology, and so on, but the division of labor in teaching seems to prevent these different topics from being combined into a whole. In fact, some of the most important and natural questions are stifled because they fall on the wrong side of topic boundary lines. Algebraists do not discuss the fundamental theorem of algebra because “that’s analysis” and analysts do not discuss Riemann surfaces because “that’s topology,” for example. Thus if students are to feel they really know mathematics by the time they graduate, there is a need to unify the subject.

Also spricht, not Zarathustra, but John Stillwell, Professor of Mathematics at Monash University (Melbourne, Oz) and the University of San Francisco.  More of him later.



About two years ago, at Reading University, I gave my last lecture on History of Mathematics.  Later that year I retired, and my department closed on the same day (remember Harpo Marx holding up the bank?) I now look back on four years of teaching the subject.

One half of the course was presented by the other lecturer, who majored on the development of the calculus, focussing especially on Newton and Leibniz.  The rest of the field was more or less open to me.   At the start, we were expecting a good turnout of 3rd year physicists as well as mathematicians, and much of my material was aimed at physicists, in particular the development of mechanics, and the 19th century mathematics that was there waiting to find fruitful application in the fields of quantum mechanics and relativity.  However, as the take-up from physicists was small, in subsequent years my material moved more towards the “core” of a mathematics course.

There are many good histories of mathematics which can be mined for material for a course: those by Kline, Katz, Boyer and Burton are especially good.  However, there are a few books which, while not being comprehensive histories, really do pick out the salient material.  If I had come across them earlier, this might have been instrumental in improving my output.

The great master of this type of writing is William Dunham of Muhlenberg College in Pennsylvania, and I will major on four books of his.  The first two are very inexpensive, and I will only present a few flying snapshots.

(1) Journey through Genius: The Great Theorems of Mathematics

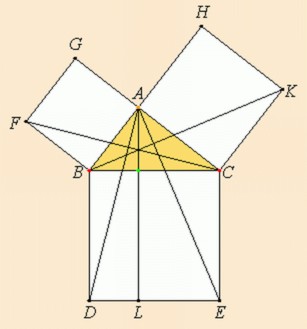One of the great grinds that schoolchildren of yore had to face was proving the Pythagorean theorem, according to Euclid.  This involved a diagram which Russian schoolboys used to refer to as “Pythagoras’s Pants”.  Euclid’s Elements is, as it comes, a very dry book indeed, and it takes a master to present it in such a way that it comes alive.  Dunham “animates” Euclid’s method better than I have encountered anywhere else.

Now we all know (I hope) that the circumference of a circle is 2πr and its area is πr2.  Euclid can tell you that the circumference is proportional to the diameter, and the area to the diameter squared, but is it the same “pie” in both?  Euclid does not tell us, but Archimedes does, and here we are told how he did it.

The Binomial Theorem was something I did at school, and could not grasp comfortably.  If I had known, as explained here, how Newton had seized it and applied it to fractional and negative exponents, I might have had much less of a struggle.

(2) The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems, and Personalities

This one, again inexpensive, is almost like a “David Attenborough highlights of mathematics”, ranging from theorems to personalities.  Again, Archimedes figures here, this time how he derived the surface area of a sphere.  

There are also many interesting biographical notes nicely blended with the mathematics.  One of the most interesting is that of Bertrand Russell (of whom a friend of mine has remarked to the effect that he could at one moment be so brilliantly right and in the next so dazzlingly wrong!)

(3) Euler: The Master of Us All (Dolciani Mathematical Expositions, No 22)

This one is from the Spanish resort of Costa Bit More, however, it is value for money.  It has eight main chapters, headed Euler and:

Number Theory / Logarithms / Infinite Series / Analytic Number Theory / Complex Variables / Algebra / Geometry / Combinatorics.

The Complex Variables chapter was the one I really took to.  Complex Numbers only started to emerge shortly after Columbus reached the Americas, and after about two hundred years mathematicians had only, so to speak, begun to settle west of the Appalachians.  Euler single-handedly drove the wagon train across the continent and reached the Pacific.

The Scottish philosopher William Stirling Hamilton (1788 – 1856) wrote:

The process in the algebraic method is like running a railroad through a tunneled mountain; in the geometrical like crossing the mountain on foot.  The former carries us by a short and easy transit to our destined point, but in miasma, darkness and torpidity, whereas the latter allows us to reach it only after time and trouble, but feasting us at each turn with glances of the earth and of the heavens, while we ... gather new strength at every effort we put forth.

In geometry we are treated to two delights.  One is a proof in pure Classical Greek Style of Heron’s formula for the area of a triangle, and the other is an algebraic account of the Euler Line joining three centres of a triangle (his successors discovered one more).  The classic geometers tended to look down on the algebraists, but anything mathematical was grist to Euler’s mill.

One would think that number theory, dealing only with integers, and analysis, dealing with the continuum, were as unrelated to each other as could be. When I was laid up with a broken ankle, our Physics Society presented me with a copy of Simon Singh’s Fermat’s Last Theorem.  Well on into the book, I learnt that proving this theorem (a gem of number theory) required recourse to elliptic integrals (the point in analysis where one is starting to get above the tree line.)  Dunham’s chapter Euler and Analytic Number Theory shows how two such diverse branches of mathematics started to reveal their mysterious underlying connections.

(4) The Calculus Gallery: Masterpieces from Newton to Lebesgue

This is one I acquired a few days ago, and I’m only just getting in to it.  In order to minimize the background required by the reader, Dunham sticks to real analysis, a remarkable restriction considering that he is a complex number mathematician par excellence.  It shows how, over more than two centuries, mathematicians laboured to put the foundations of that wonderful discovery, the calculus, on to a firm logical basis.  And it does so without that ferocious symbolism that would scare away many people (myself among them) from doing a university course in mathematics.



Now to two other books.

Unknown Quantity: A Real and Imaginary History of Algebra by John Derbyshire is not only a history, but an ideal stepping-stone for anyone who is confronted with a course in modern algebra or Galois theory that’s going too fast to jump on board.  Those into that kind of mathematics will wonder if my inclusion of the word “ideal” is a pun, and indeed it is.  

Mathematical ideals grew out of the Ideal Numbers of Ernst Kummer.  Now mathematics undergraduates will get ideals thrown at them straight away, but to me they (the students) are “reptiles”, whose eggs can hatch directly on land.  I am an “amphibian”, and to take on these ideas I need to go through something of a historical stage in my understanding.  So for my fellow “tadpoles”, may I recommend 

Yearning for the Impossible: The Surprising Truths of Mathematics by John Stillwell

which treats them in one of the chapters.  There are also in this book many other wonderful connections between different topics of mathematics.

If you find teaching or learning mathematics makes your brain feel arthritic, these are the books to lubricate your cerebral joints!

 * * * * * * * * * *