Was Einstein wrong about ? 

No, the equation correctly relates an objects rest mass to its energy content. However, in 1952, Herbert Ives published Derivation of the Mass-Energy Relation in the Journal of the Optical Society of America. It purports to show that Einstein's derivation was invalid because Einstein committed the error of begging the question mathematically (its in the Appendix if you're curious). According to Ives, Einstein implicitly assumed that E=mc^2 in his derivation of E=mc^2. I believe Ives' mistake results from the false assumption that Einstein put in the relativistic equation for the kinetic energy of a particle, when he merely notes that his expression resembles it. Recall that Einstein argues that the energy in the last step is purely kinetic because it is constructed from terms that are only due to the motion of the box. He never puts in the formula for relativistic kinetic energy explicitly, as Ives does. Instead, he makes an a priori argument that the term is kinetic, expands it, and then compares it to the classical formula for kinetic energy. The classical formula is appropriate because the box is moving slowly. A criticism of Ives by John Stachel and Robert Torretto expertly confirms this analysis, "the reader should note how carefully Einstein avoids any assumption about how the relativistic energy depends on velocity, mass, or any other parameters..."(Stachel. Einstein from B to Z. page 218)

I should add that, even if the derivation is incorrect, even if all derivations are incorrect, the equation has been verified countless times in countless controlled experiments (for example, it is verified constantly at particle accelerators).    

Again, if properly interpreted -as giving the relationship between an objects rest mass and its energy content -the equation is correct, but according to esteemed physicist, Tony Rothman, although Einstein's 1905 derivation of is correct, Einstein was mistaken about why it was correct. But, before I address that, let me explain why I'm interested in Rothman's opinion. In my last blog, I presented Einstein's first derivation of E=mc^2 and wrote that Einstein oppositely oriented the light rays in his thought experiment to "simplify the mathematics". It does simplify the mathematics, but if the same argument is applied to one light ray, then the mathematics does not give the same result because it lacks a cancellation of terms and, therefore, the orientation of the light rays is essential. First, I'll show this by doing the calculation with one light ray and then I'll try to explain physically why the orientation of the rays is essential to deriving the relativistic effect. Finally, I will ask the reader to comment on my argument because, according to Rothman, Einstein was wrong and the derivation isn't relativistic.   


I've searched my local library for a more detailed evaluation of Einstein's paper, but the best reference I've found, the only reference in fact, is Abraham Pais' great scientific biography of Einstein, Subtle is the Lord. It has a quick encapsulation of the paper that mentions the opposite orientation of the light rays but doesn't explain it or the physical meaning of the cancellation.  According to Pais, Einstein had doubts about the paper.

But Einstein was not quite sure. In the fall of 1905 he wrote to Habicht, "The line of thought is amusing and fascinating, but I cannnot know whether the dear Lord doesn't laugh about this and has played a trick on me..." 

Unlike the original thought experiment, begin by assuming that a single light ray leaves the right side of the box.

Then 



and

because 



and recall that  

 

so




And applying the argument from the last blog gives the following expression for the difference in the kinetic energy of the box, due to the observed motion of the box, after the emission of a light ray from it.



If the light ray is going in the opposite direction then, -v/c is replaced by v/c and this is why oppositely orienting the light rays produced only the kinetic energy term of the form 1/2mv^2 (where m=L/c^2) through cancellation. Einstein pointed his light rays in opposite directions to cancel out this term. The derivation depends crucially on this cancellation.

I've shown what pointing the light rays in opposite directions accomplishes mathematically, but what is the physical interpretation of this cancellation? Here is my initial answer (see * and ** below for my final answer).

At the time I was attempting to calculate 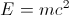 from the quantum formula  where h is Plank's constant and f is the frequency of the light wave and E is the energy of a photon. Instead of using the formula for energy shift, I applied the relativistic Doppler shift formula to f. This gives the shift in energy, E, of due to the shift in frequency, f.  That is very simple to do because the equation for relativistic frequency shift is



Because this has the same form as the energy shift formula seen in my last blog (Einstein derived that formula from this one in On the Electrodynamics of Moving Bodies) taking the energy, L, equal to hf, produces the same result as before. Therefore, again, for the one light ray case, 

 


it appears that oppositely orienting the light rays serves to cancel out the first order shift due to the non relativistic Doppler effect and leave the higher order shift due to relativity. This is confirmed by noting that the purely relativistic transverse Doppler effect is given by 





Unlike the nonrelativistic case, relativity includes a shift that is not due to longitudinal motion. This transverse Doppler Effect is purely relativistic, invoking it implies that v is large enough that v^/c^2 is no longer negligible. It is the observed frequency shift of a light ray as the observer passes the axis of the light ray at a 90 degree angle with velocity, v. We could redo the original thought experiment again, this time considering the mass loss due to the transverse effect and this gives the original result. This is a sketchy argument, meant only to be suggestive of a possible rigorous argument to be developed later, but- at the very least- relativity introduces a term that doesn't cancel out (how could a transverse effect "cancel out"?) and therefore relativity predicts mass loss via radiation.





But, then I read this in an article on physicsworld.com, titled Did Einstein discover E = mc^2? , 

While Einstein's celebrated 1905 paper, "On the electrodynamics of moving bodies", clearly laid down the foundations of relativity by abandoning the ether and making the speed of light invariant, his derivation of E = mc^2 did not depend on those assumptions. You can get the right answer with classical physics, says Rothman, all in an ether theory without c being either constant or the limiting speed. "Although Einstein begins relativistically, he approximates away all the relativistic bits, and you are left with what is basically a classical calculation."

So do I have it exactly reversed? Instead of deriving a relativistic result Did Einstein actually "approximate away all the relativistic bits"?!  

I haven't found a more detailed mathematical argument by Rothman.

 What do you think?  

* In my last blog, I listed the assumptions implicit in the derivation. I should have included conservation of momentum. Based on the comment by Anonymous below, making the two light rays oppose each other implies, from conservation of momentum, that the total momentum of the light in the box frame of reference is 0. If only one light ray leaves, then the momentum of light is positive and conservation of momentum implies that the box has gained momentum ("recoiled"). That would, at the very least, complicate the derivation and would be reason enough to oppositely orient the light rays. But, on the other hand, the amount of recoil from light would be negligible. However, assuming that the recoil is negligible would have been equivalent to assuming that the "mass" or energy content of light is small and that is what Einstein was attempting to prove quantitatively. 

 ** In quantum mechanics E=pc=hf implies that p=(h/c)f and in units where h/c=1, p=f. This suggests that the results about Doppler shift can be restated in terms of momentum and recoil. Because non relativistic Doppler shift is given by


and p=f implies

 and for the left moving light ray

and, because 

In the Box Frame of reference, the momentum is cancelled and the box experiences no recoil, but in the frame of reference moving with velocity, v, the total momentum shift is  

 


the light itself has a net momentum in one direction. 

But recall that, in the original derivation, (1+v/c) and (1-v/c) were added, not subtracted (energy is a scalar), and that resulted in cancellation. Therefore, the cancellation of the v/c terms is a trivial consequence of the condition that the total momentum of light is cancelled so the box isn't recoiled (if this isn't obvious to you, take the v in the total momentum shift formula equal to 0 or think about what happens as v gets smaller). The box must not recoil because it was essential to Einstein's original argument that the kinetic energy of the box is only due to the relative motion of Moving Frame with respect to the Box Frame. 

The net momentum shift calculated above leads to another, manifestly nonrelativistic, derivation of E=mc^2 based on the the fact that p=E/c. 

***I'm still unsure of how the original derivation can really be said to "approximate out all of the relativistic bits" when the final step depends on expansion of the explicitly relativistic gamma factor. Although the same argument probably goes through by merely considering c to be very large, the introduction of the gamma factor itself would not have been introduced without relativity.  But, until I've read more about it, it is probably reasonable to assume that I'm over-analyzing his statement. He did say "basically" nonrelativistic. 
  
****Reading the earlier paper, On the Electrodynamics of Moving Bodies, I came across the relativistic formula for the kinetic energy of a particle. It includes mc^2 and it is probable that Einstein intuited that mc^2 must be the energy content of the body from that and simply designed his thought experiment such that this result came out.

*****Today, 5/25/2012, Stanford uploaded a lecture by Leonard Susskind that begins with a derivation of the relativistic doopler effect. 

******Sixty Symbols on E=mc^2