Fortunately, science does not work that way. Science is no democracy, and we do not render a theory invalid by popular vote. Einstein's theory of relativity has stood the test of time and its correctness is beyond any doubt. But... there is an issue with what is arguably the most famous equation in the history of natural sciences.
So what is the problem with Einstein's mass-energy relation?

Well, to put it bluntly, there is no such thing as a mass-energy relation. What does exist is a mass-energy-momentum relation. The equation Einstein came up with more than a century ago can be considered a degenerate form of the mass-energy-momentum relation for vanishing momentum. Einstein was very well aware of this, and in later papers repetitively stressed that his mass-energy equation is strictly limited to observers co-moving with the object under study. However, very, very few people seem to have paid attention to Einstein's warnings, nor to any of the more recent warnings. Even worse, the vast majority of authors of popular science books take great liberty in applying E=mc2 to objects moving at speeds close to the speed of light, and then declare mass to increase with velocity in an attempt to recover consistency in what has become an incoherent mix of relativistic and Newtonian dynamics. Theoretical physicist Lev Okun refers to this practice as a “pedagogical virus”.
What I consider truly amazing, is how few people are aware of the mass-energy-momentum relation. In contrast to the widely popularized equation E=mc2, the mass-energy-momentum relation is a direct result of the fundamental principles of relativity theory, and provides true insight into the basics of relativity. Moreover, and contrary to what one might expect, the mass-energy-momentum relation is far from complicated. In fact, the mass-energy-momentum relation does not even need a mathematical equation, a simple drawing with annotations suffices.
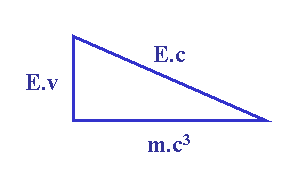
Einstein meets Pythagoras: the mass-energy-momentum relation. In the rectangular triangle, the hypotenuse represents energy times c (c denoting the speed of light), the vertical edge momentum times c2, and the base mass times c3.
The above figure graphically captures the mass-energy-momentum relation for a particle of mass m and total energy E, moving at velocity v. The parameter c denotes the speed of light. Shown is a right triangle with labeled edges. The hypotenuse labeled Ec is proportional to the energy of the particle, and has length energy E times speed of light c. The vertical edge labeled Ev is proportional to the momentum of the particle and has length E times v. Finally, the base labeled mc3 is proportional to the mass of the particle and has length m times c3.
The full relativistic kinematics is captured in this annotated triangle. Knowing two out of the three quantities mass, energy and momentum, using this simple diagram one can easily derive the third. For instance, suppose one wants to know the total energy of a particle, when given that it moves at a velocity of 3/5 the speed of light. With v:c equal to 3:5, it is clear that the vertical edge Ev and the hypotenuse Ec are in the same ratio. Applying the Pythagorean theorem immediately leads to the conclusion that we are dealing with a 3:4:5 triangle. Hence, the hypotenuse is 5/4 times the base: E = 5/4 mc2. Who told you relativity theory is heavy stuff?
We can also use the above triangle to derive some generic relativistic results. For instance, as the vertical edge can not be longer than the hypotenuse, one of the core axioms of relativity follows: no particle can move with a speed v larger than the speed of light c. Notice that to achieve this result, we don't need any misleading constructions like 'mass increases with velocity'.
Also the extreme case of m = 0, applicable to massless particles like photons, is well captured in the triangle. For m = 0 the triangle collapses to a vertical line element and it follows immediately that Ev = Ec or v = c. Massless particles move at the speed of light.
Needless to say that Einsteins mass-energy relationship is captured as well in the special case Ev = 0 (i.e. for the triangle collapsing into a horizontal line element). For those brave enough to battle some math equations: it can also be shown that when Ev is non-zero but much smaller than Ec, the non-relativistic (Newtonian) limit is firmly captured in the mass-energy-momentum triangle. For Ev << Ec the triangle takes a flat shape with Ec ≈ mc3 so that the Pythagorean equation can be written (Ev)2 = (Ec)2 – (mc3)2 = (Ec + mc3)(Ec - mc3) ≈ 2mc3(Ec
– mc3). Hence, Ec – mc3 = (Ev)2/2mc3 or E = mc2 + (Ev)2/2mc4 ≈ mc2 + (mc2)2v2/(2mc4) = mc2 + mv2/2. If you managed to follow this math reasoning, surely you will recognize the well-known Newtonian kinetic energy expression in this result.
A few more relativistic insights are captured in the mass-energy-momentum triangle. For instance, the mere fact that the momentum edge is labeled not mv (nor mc2v) but rather Ev is significant. It stresses the fact that the total energy (and not mass) is a measure of inertia. Once one realizes this, it should be clear that statements like “mass increases with velocity” are plainly wrong.
You might wonder, why is it that this mass-energy-momentum relation can be represented in a simple rectangular triangle? This question brings us to the heart of Einstein's relativity theory. In four-dimensional spacetime, energy and momentum lose their meaning as separate quantities. Instead, a four-component spacetime vector emerges that describes energy and momentum in a unified fashion. In loose loose terms one can envision this spacetime vector as a flow of energy at speed v in space and speed c in time. The space (Ev) and time (Ec) components of this energy-momentum vector do depend on the frame of reference of the observer, but the length of this vector is an absolute quantity, that is independent of the choice of observe. This quantity is called mass.
In a normal Euclidean space, the length of a vector is determined by a Pythagorean sum of the components. Spacetime vectors behave subtly different as the space and time components contribute to the vector length with opposing signs. As a consequence, when grouped into a space and a time component, the length of a spacetime vector is given by the Pythagorean difference of the two components. What results is a rectangular triangle with the length of the spacetime vector being represented by one of the short edges.
Will we ever see mass-energy-momentum triangles replacing E=mc2 as slogan on t-shirts? I don't hold my breath. A technically superior product in itself is unlikely to replace a strong brand. And “E=mc2” certainly is a strong brand for 20th century physics. In fact, it is more than that. A true symbol and icon of mankind's intellectual achievements. The fact that it is more than often represented in an inconsistent way is a shame, but can not take away that luster.
--- Follow-up posting: click here ---





Comments