In his book "Everything's Relative - And Other Fables From Science And Technology" Tony Rothman writes:

 "[The term] 'special relativity' is probably the greatest misnomer in the history of science"

I wholeheartedly agree. Amongst all scientific terms, the single word 'relativity' stands out as absolute record holder for triggering an astonishing amount of utter nonsense. 

It was not Einstein but Max Planck, who introduced the term 'relativity theory'. That was in 1906, the year following Einstein's annus mirabilis. Despite Einstein's opposition, the name stuck. Years later Einstein surrendered, and from 1911 onward he started to use the term 'relativity theory' himself. But he never felt comfortable with the term, and in his writings he always put the words in quotes.

'Relativity theory' deals with the description of physical phenomena in space-time, and the shadows these phenomena cast in space as well as in time. These shadows is what we tend to perceive, yet they are not absolute, but rather dependent on one's point of view. However, by quantifying these phenomena not in terms of these shadows, but in terms of an objective space-time formulation, an absolute description emerges. 

So, the strength of 'relativity theory' is that it identifies space-time invariants, absolute values independent of point of view. It is for this reason that 'space-time invariants theory' would have been a much better description for Einstein's brainchild.*

Sounds like hanky panky?

Let's bring the issue into the realm of everyday phenomena. 

Pythagoras - The First Relativist

Imagine two persons, Alexios and Berenice, attempting to quantify the size of a straight fence. 

Alexios makes the claim "If I take 20 steps sideway, I reach one end of the fence, and if I make 15 steps forward I reach the other end. The fence is 20 steps wide and 15 steps deep."

"You are wrong", answers Berenice. "I carefully counted my steps: it takes 24 sidesteps to reach one end, and 7 steps forward to reach the other end. The fence is 24 steps wide and 7 steps deep."



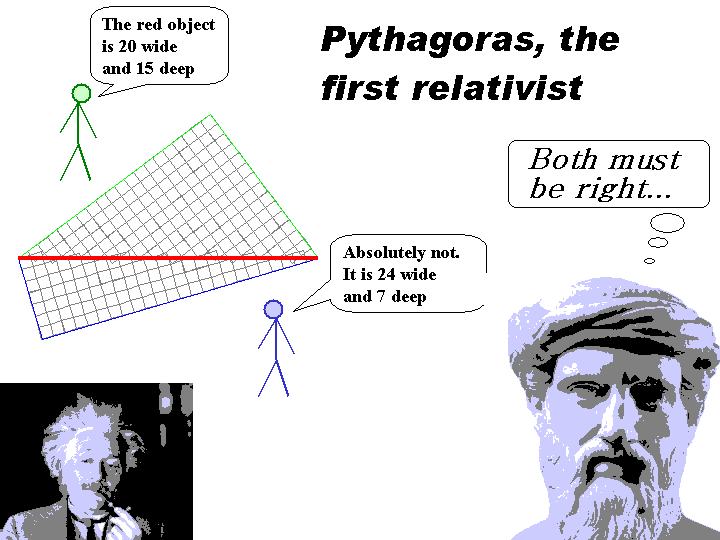
Along comes a guy named Pythagoras. "You are both right", he declares. "I happen to have studied this situation. The length of the fence is invariant and objective, but your measurement outcomes in terms of steps sideways and steps forward will depend on your orientation."

"Wow, that's weird" Alexios remarks. "How can we both be right? Our numbers are different, Berenice is telling me the fence has shrunk in depth and dilated in width!""

"Well" answers Pythagoras, "as strange as it might seem, there is no real contradiction. According to a theorem I derived, your descriptions of the fence are relative, yet the fence itself is absolute and.."

".. Ahh, it's all relative?" interjects Alexios.

"I like that term!" exclaims Berenice. "Let's call his theorem on fence compression and dilation 'the relativity theorem'!"

"Good idea", confirms Alexios. And off they went.

Amazing Alignment

Suppose this theorem you learned at math classes would have gone under the name Pythagoras' relativity theorem. Would that have triggered a whole industry of misapplication of this mathematical result ranging from simple crackpottery to straight abuse on moral matters?

That seems very unlikely.

As Hermann Minkowski clearly demonstrated, Einstein's theory is a straightforward extension of Pythagoras into the realm of space-time. And this in itself stresses a key difference between Einstein's results and plain-vanilla Pythagoras. The latter is intuitive as it refers to space only, while Einstein's theory applies to space-time and is highly counterintuitive.

We are used to rotating yardsticks in space so as to conveniently measure the length of fences. Yet, we are much less used to rotating yardsticks in space-time. 

Rotations in space-time correspond to changes in speed. So we are talking about measuring sizes when speeding along the object to be measured. And the issue is: in our daily lives we never speed. For all practical purposes we are at standstill compared to each other and compared to the objects around us. 

In other words, referring again to the fence analogy that made it clear how orientations influence measurements: we take space-time measurements only in one orientation. This space-time orientation is common amongst all of us, and we refer to it as the orientation 'forward in time'. During our lifetime we typically move some seventy years in this direction. Yet, we hardly explore any of the orthogonal directions. The furthest some humans have gone away from other humans in these orthogonal directions is about a second. And we are talking here about the very few selected individuals who made it to the moon. A huge concerted effort and lots of tax money brought them about a second away from the seventy year long path that is provided to all of us free of charge. 

We might have hugely different opinions and strongly orthogonal views, when it comes to our path in space-time we are better aligned than a laser beam. All seven billion of us, no exception!

Space-Time Pythagoras

Lacking the capability to freely orient ourselves in space-time, we also lack the intuitive notion of space-time rotations. We are like Alexios, but without the benefit of a Berenice who can challenge his point of view. 

But there is one difference between us and Alexios and Berenice: for more than a century now, we have a consistent picture of space-time rotations, and we know exactly how to measure space-time distances despite the fact that we lack diversity in orientation. 

Key is to measure both space and time directions just like Alexios and Berenice measured width and depth. Using these measurements, we reconstruct the true space-time size using Einstein's space-time Pythagorean theorem. Recalling Pythagoras for spatial measurements:

SIZE² = WIDTH² + DEPTH²

the space-time Pythagorean theorem differs in one important aspect: time and space behave differently thereby causing opposite signs in the sum of squares on the right-hand side:

AGING² = DURATION² - DISTANCE²

Note that we have identified the space-time size as 'aging'. Where in the fence analogy the true size of the fence is the size measured along the direction of the fence, similarly in space-time true size is measured by orienting the measurement device in the same space-time direction as (i.e. moving along with) the object. As remarked earlier, this direction is the time direction common to the object and the observer. 

What this equation tells us is that while different observers might measure different durations and different distances of a path in space-time, they will all agree on the difference between their squares, the aging along that space-time path.

More Pythagorean Relations

The beauty of Einstein's theory is that it applies more widely than just to distance and duration. Other physical parameters span similar four-dimensional spaces (referred to as Minkowski spaces) to which the same relativistic Pythagorean theorem applies. 

A well- known example is provided by the physical parameters conjugate to time (energy) and conjugate to distance (momentum). So we have a relativistic Pythagorean theorem for energy-momentum space that reads:

MASS² = ENERGY² - MOMENTUM²

Again, the left-hand side and right-hand side of this equation are invariants: quantities independent of point of view. Mass is an objective quantity and so is the difference between the squares of the energy and momentum.

For small relative velocities between object and observer (and as remarked above, we are invariably in a state of rest compared to all sizable objects around us), this reduces to:

MASS = ENERGY

An equation most people are more familiar with when a conversion factor c^2 related to the use of clumsy units is included. 

Relativistic Pythagorean theorems also extend to electromagnetism and are deeply rooted in quantum field theory. In fact, all of modern physics is formulated in a space-time description that unifies a huge range of physical concepts. 

Whatever the name, 'relativity theory', 'theory of absolutes', 'invariants theory': modern physics is unthinkable without the Pythagorean space-time theorem. 

Notes

* A proposal along these lines was actually made in 1910 by mathematician Felix Klein.


The Hammock Physicist on: E=m.c², Entropic Gravity, Entropic Force, Shut Down LHC?, Game Theory, Metric Vs Imperial, Big Bang, Dark Energy, Chaos And Time's Arrow, The Physics Arena, Square Root Of The Universe, Physics In A Nutshell, The Longest Path, Hotel Boltzmann, Quantum Telepathy, Quantum Viruses, QHD, Fibonacci Chaos, Counting A Black Hole, Entropic Everything, God, Godel, Gravity