Imagine you are tasked to build the ultimate computer memory. You are provided with an unlimited budget and all the resources you need. 

How big a memory capacity could you build? 

You decide to put it to a test. Being a clever cookie, you don't just order a huge pile of computer memory chips. You know you can do far better than relying on standard components. So you start designing and building ultra high density storage devices: high energy modules each capable of storing an insane amount of information. Soon you have set up a manufacturing line for these memory devices, and you find yourself managing a huge workforce connecting the devices together into one single big memory bank. An immense memory structure starts to grow. In the months following, modules continue getting added, and the total data storage capacity keeps growing proportional to the volume of the structure. 

Then one day a nerdy guy in a raincoat, who introduces himself as 'Gerard', comes along. He looks with interest at the huge memory structure evolving, and scribbles fanatically on a notepad. Before he leaves he takes you apart and makes a puzzling remark: "According to the holographic principle there is a fundamental limit to the information capacity of space, and this limit increases with the surface area. Because volume increases more rapidly than surface area, at some point nature will play a very dirty trick on your growing volume of memory."



Gerard, the prophet of doom, during his visit, depicted in front of the memory volume under construction. Clearly visible are the liquid nitrogen supply pipes required to cool the structure.

You have no clue what the guy is talking about, and immediately after he leaves the construction work again requesting your attention. Soon you forget about the strange encounter. Months go by, and the memory structure keeps growing and reaches truly gargantuan proportions. Then one day, 21st December 2012, early in the morning when you are in your office, and just when you bring a cup of coffee to your mouth, a deep rumbling noise emerges from the construction site... 


Quantum meets gravity
The holographic principle is a fundamental result obtained by combining key features of the two pillars of modern physics: quantum theory and general relativity. Two pillars which, despite huge efforts over many years, remain incompatible. Any fundamental result applicable to the 'region of overlap' between quantum physics and general relativity therefore constitutes a major breakthrough. Unfortunately, we don't have many of these, and surely the holographic principle stands out as the prime example of such a breakthrough. 

Below I will demonstrate that the holographic principle boils down to 'counting a black hole'. It is about deriving the number of quantum degrees of freedom (or equivalently, the number of bits) that need to be specified to describe the physical state of a black hole in all its details.   

Consider a spherical region of space. Quantum physics tells us that a quantum of energy localized in this region can not be arbitrarily small. The minimum energy of such a quantum is inversely proportional to the circumference of the region. Make the circumference twice the size, and the minimum quantum shrinks in half. What happens when one creates a quantum containing less than the minimum energy? Well, nothing particular happens, it is just that Heisenberg's uncertainty principle will prevent such a low-energy quantum to fit within the spherical volume specified.

Ok, so we accept that a finite region can only contain energy in steps, and that the step size is inversely proportional to the circumference of the region. However, things become really interesting when we consider the other end of the spectrum: the maximum energy that can be contained in a finite region.
 
Einstein's theory of gravity tells us that there is indeed a limit to the total amount of energy that can be stored within a region of space. This maximum energy is proportional to the region's diameter. Give the region twice the diameter, and the maximum energy doubles. What happens if one keeps on adding energy into a volume of space such that the maximum energy content gets reached and then exceeded? The German physicist Karl Schwarzschild worked this out for us during World War I, when fatally ill and stuck in the trenches at the Russian front. (Anyone got a better candidate for the title 'most dedicated scientist ever'?) What Schwarzschild found was that when the maximum energy of a spherical volume is reached a black hole must have formed that fills the whole volume. When more energy gets added, this black hole starts to outgrow the volume, with its energy content spilling over into the neighboring volume.  


Human genius meets human cruelty: the idea of a black hole originated in the trenches during World War I. 
   
The conclusion is inevitable. A finite volume not only enforces energy storage in finite steps, but also limits the total energy that can be stored. We can combine these constraints imposed by quantum theory and gravity theory, respectively, by calculating the ratio of the total maximum energy over the minimum quantum. In doing so a constraint emerges on the number of quanta that can be contained in a spherical region. This maximum number is proportional to the product of the sphere's diameter times its circumference or, in other words, proportional to the surface area of the sphere.  

This constraint that tells us something deep and profound about the characteristics of the still elusive theory of quantum gravity. To describe the full physics taking place within a spherical region of space, you need to specify all the quanta. This requires a number of bits proportional to the surface area of the region. In other words: what happens within the region can be thought to be encoded in surface bits. If that is indeed true, the fundamental laws of physics that describe what happens within a given volume should take the shape of some kind of fast-paced quantum game-of-life at the surface of the volume. The phenomena we observe within a region of space are thereby reduced to a mere holographic projection of a quantum game taking place on the region's boundary. 

And that, in a nutshell, is the holographic principle. That was not too difficult, was it? Independent of your answer to that question, you probably want to skip the rest of this blog post. 

But for those who insist on seeing some math, be my guest:


Bohr's black hole 
Where the hydrogen atom formed the playground that allowed the derivation of quantum mechanics, the Schwarzschild black hole similarly acts as a playground for quantum gravity models and for the holographic principle in particular. A simple derivation of the fact that the maximum entropy of a region in space is proportional to its area goes along the lines of the well-known Bohr model of the hydrogen atom. Like the Bohr model, the derivation given below is far from rigorous, yet it does correctly represent the key physics ingredients. 

Here goes.

We start by observing that according to Newton's theory of gravity an object of a certain mass will prevent slowly moving objects in it's vicinity to escape from it's gravitational attraction. Starting from Newton's one-over-the-distance gravitational energy and doing the math, it follows that any objects within a distance R from a mass M and moving at a velocity less than the escape velocity v determined by

v² = 2 G M / R

will be gravitationally bound to the mass M. To prevent the formation of a black hole, we require the escape velocity v to be smaller than the speed of light c. We also use Einstein's E = M c² to eliminate M in favor of E, so as to make explicit that not just rest energy (mass) but any form of energy results in a gravitational attraction. It follows that the amount of energy that can be stored in a spherical region of radius R is bound by

E 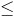c⁴ R / 2G 

When this bound is saturated, a black hole of radius R has formed.

Now we need to bring energy quantization into the picture. Einstein thought us that light of frequency f comes in photons with energy hf each, where h is Planck’s constant. The lowest energy quanta that can be accommodated in a spherical region of given size are photons with a wavelength equal to the region's circumference. Equating the product of the wavelength and the frequency to the speed of light, it follows that the energy content of the region is quantized in steps

dE 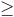 hc / 2pi R

Combining the last two equations, it follows that a spherical region bounded by an area A can contain a number of quanta equal to 

E / dE 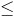c³ A / 4 G h 
   
If each quantum carries one nat of information, it follows that the entropy of a spherical region with area A is bounded by

S 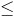k c³ A / 4 G h 

where k is Boltzmann's constant. Again, the bound gets saturated (the equality sign applies) once a black hole with surface area A has formed. 

Notwithstanding the hand-waving nature of the derivation, and although we have used Newton's law of gravity rather than Einstein's, and despite having applied a Bohr-like description rather than a full quantum treatment, the correct holographic description results: an entropy bound proportional to surface area. Also the constant of proportionality between entropy and surface area is correct within a factor of 2 pi (note that the constant h features in the equation, rather than h-bar). 

Not too bad for a simple back-of-the-envelope estimate of a fundamental result at the tricky intersection of quantum physics with gravitational physics, a dark enigmatic area considered by many the exclusive domain of superstring theory.